3387
Trajectory correction in high-resolution gated golden-angle radial Dixon imaging using the gradient impulse response function1Department of Diagnostic and Interventional Radiology, Technical University of Munich, München, Germany, 2Philips Research Laboratory, Hamburg, Germany, 3Philips Healthcare, Best, Netherlands
Synopsis
Stack-of-stars-type radial k-space trajectories employing golden-angle ordering have been becoming popular for either free breathing or navigator-gated volumetric T1-weighted imaging of the abdomen and heart. Most methods for compensating radial k-space trajectory errors induced by eddy currents and system delays are based either on the acquisition of calibration lines with opposite polarity or on the processing of approximately anti‐parallel spokes from the actual radial acquisition. This work shows that a trajectory correction based on a gradient system impulse response function improves image quality in high-resolution gated golden-angle radial Dixon imaging.
Purpose
Golden-angle-ordered radial acquisitions have become popular in MRI of moving organs due to their continuous coverage of the k-space center1,2. In particular, stack-of-stars-type (SoS) radial k-space trajectories employing golden-angle ordering have been used for either free breathing or navigator-gated volumetric T1-weighted imaging of the abdomen and heart3,4. A major challenge of radial acquisitions is that changing the read-out gradient orientation for each radial spoke makes the k-space trajectory vulnerable to inaccuracies of the gradient chain5. Previous methods for compensating for such k-space trajectory errors have focused on the determination of gradient timing errors based either on the acquisition of calibration lines with opposite polarity6 or on the processing of approximately anti‐parallel spokes from the actual radial acquisition7. However, the above methods simply account for delays inducing a global uniform k-space shift along each spoke and do not consider any changes in the sampling density along each spoke (e.g. due to short time constant eddy currents). Such effects could become particularly important in high-resolution radial imaging8 and could be corrected by a calibration scan that fully characterizes the gradient system impulse response function (GIRF)9-11. The purpose of the present work is to perform trajectory correction in high-resolution gated golden-angle radial Dixon imaging based on the GIRF measured using a thin slice method.Methods
k-space spoke alignment: Eddy-current induced gradient delays can cause k-space shifts along the readout direction. The used radial acquisition scheme allows for a simple retrospective phase shift estimation. Due to the 360˚ rotation of the spokes in the SoS, each spoke can be correlated with an approximately anti-parallel spoke. The k-space shift k0 between two spokes can be modeled by a linear phase in image space according to the Fourier shift theorem. k0 was determined for each spoke by solving the following optimization problem:$$$k_0=\underset{k_0^*}{arg\,min}\left\Vert\frac{\partial\left|\mathfrak{F}\left(p^+e^{-i{\pi}{k_0^*m}}\right)\right|}{\partial{k}}-\frac{\partial\left|\mathfrak{F}\left(p^-e^{+i\pi{k_0^*m}}\right)\right|}{\partial{k}}\right\Vert_2$$$
where p± denote the complex 1D image space profiles measured with opposite readout gradient polarity and $$$\mathfrak{F}$$$ is the discrete Fourier transform function12. The derivative of the k-space spoke profiles makes the fit more robust and insensitive to differences in the frequency response.
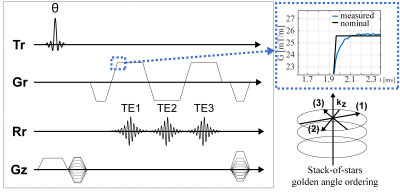
Trajectory correction: Fig.1 shows the employed SoS multi-echo sequence. A phantom-based measurement of the GIRF using a thin-slice method13 was used to characterize the gradient system. The magnitude and phase of the first order components of the GIRF were used for the correction of the readout gradient by convolving the GIRF with the input gradient waveform (Fig.1).
Simulation: Simulated k-space data of a Shepp-Logan Phantom was generated by using the NUFFT (BART,https://mrirecon.github.io/bart/) with the measured, GIRF-corrected, k-space trajectories. Images were reconstructed by using the nominal k-space trajectory with and without correcting the data with the proposed k-space spoke alignment method, respectively. The measured trajectory was used as the reference reconstruction method.
Phantom measurements: A 3D SoS 3-echo measurement (Fig.1) was performed on a 3T system (Ingenia ElitionX/Philips Healthcare/Best/The Netherlands) with a structural phantom using a 16-channel anterior coil with TE:[1.7/3.0/4.3]ms, TR:7.6ms, flip angle:10°, resolution:1x1x3mm3, FOV:300x300x240mm, duration: 5min37s.
In-vivo measurements: A gated 3-echo SoS (Fig. 1) abdominal measurement was performed on three volunteers by using a 16-channel anterior coil with TE:[1.4/2.4/3.4]ms, TR:5.4ms, flip angle:10°, resolution:1.5x1.5x3mm3, FOV:450x450x120mm, duration: ca. 5min. Complex-based water-fat separation was performed accounting for the multi-peak fat spectrum.
Results
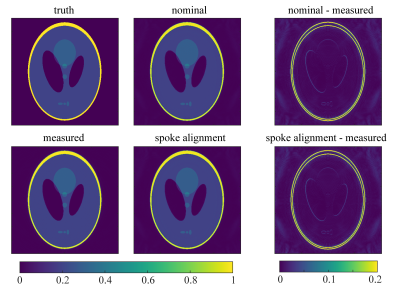
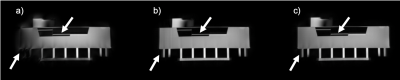
Simulation: Reconstruction results of the spoke-aligned k-space data and uncorrected k-space data were compared to the reconstructed image using the measured trajectory (Fig.2). The image reconstructed with the nominal trajectory showed blurred edges and a higher background intensity. The spoke alignment method was not sufficient to correct for these errors and the reconstructed image showed similar artifacts as the uncorrected one.Phantom: Fig.3a shows that the uncorrected source images were severely affected by trajectory errors. Edges appeared blurred and the intensity distribution was inhomogeneous within the phantom. Both methods, the k-space spoke alignment (Fig.3b) as well as the GIRF trajectory correction (Fig.3c) were able to retrieve a homogeneous intensity distribution and reduce artifacts. The GIRF corrected image successfully deblurred finer structures (indicated by arrows).
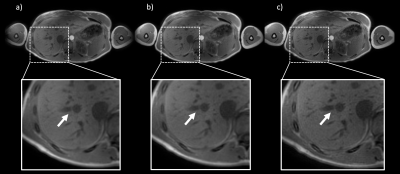
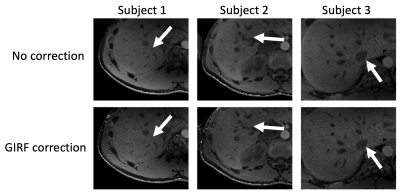
In vivo: Fig.4 shows source images of the liver reconstructed with the nominal trajectory with (Fig.4a) and without the k-space spoke alignment (Fig.4b) as well as images reconstructed with the measured k-space trajectory (Fig.4c). The GIRF corrected image (c) appeared sharper than (a) and (b). Uncorrected and GIRF-corrected water images were compared in Fig.5 for three different subjects. In all three cases, the effective image resolution was increased by the GIRF correction and vessel structures appeared sharper compared to the uncorrected images.
Discussion & Conclusion
Eddy currents and system delays cause artifacts in radially sampled images. The present work shows that with a simple GIRF measurement and standard scanner hardware the real k-space trajectories can be estimated. The GIRF corrected trajectories reduced signal energy in the background and blurring in the reconstructed images. The proposed method is also able to correct for high frequency errors which are not removed by aligning opposite spokes in k-space. However, the proposed GIRF correction does not correct for motion effects that could be corrected by using the k-space spoke alignment. A GIRF-based correction of the SoS trajectory should therefore be considered as a fast and reliable principle to increase image quality.Acknowledgements
The present work was supported by the German Research Foundation (SFB824/A9), the European Research Council (grant agreement No 677661, ProFatMRI) and Philips Healthcare. This work reflects only the authors view and the funders are not responsible for any use that may be made of the information it contains.References
[1] Block, Kai Tobias, et al. "Towards routine clinical use of radial stack-of-stars 3D gradient-echo sequences for reducing motion sensitivity." Journal of the Korean Society of Magnetic Resonance in Medicine 18.2 (2014): 87-106.
[2] Uecker, Martin, Shuo Zhang, and Jens Frahm. "Nonlinear inverse reconstruction for real‐time MRI of the human heart using undersampled radial FLASH." Magnetic Resonance in Medicine: An Official Journal of the International Society for Magnetic Resonance in Medicine 63.6 (2010): 1456-1462.
[3] Feng, Li, et al. "Golden‐angle radial sparse parallel MRI: combination of compressed sensing, parallel imaging, and golden‐angle radial sampling for fast and flexible dynamic volumetric MRI." Magnetic resonance in medicine 72.3 (2014): 707-717.
[4] Feng, Li, et al. "XD‐GRASP: golden‐angle radial MRI with reconstruction of extra motion‐state dimensions using compressed sensing." Magnetic resonance in medicine 75.2 (2016): 775-788.
[5] Peters, Dana C., J. Andrew Derbyshire, and Elliot R. McVeigh. "Centering the projection reconstruction trajectory: reducing gradient delay errors." Magnetic Resonance in Medicine: An Official Journal of the International Society for Magnetic Resonance in Medicine 50.1 (2003): 1-6.
[6] Block, K. T., and M. Uecker. "Simple method for adaptive gradient-delay compensation in radial MRI." Proceedings of the 19th Annual Meeting of ISMRM. Vol. 19. 2011.
[7] Untenberger, Markus, et al. "Advances in real‐time phase‐contrast flow MRI using asymmetric radial gradient echoes." Magnetic resonance in medicine 75.5 (2016): 1901-1908.
[8] Kronthaler, S., Rahmer, J., Börnert, P., Karampinos, D.C., Trajectory correction for ultrashort echo-time (UTE) imaging based on the measurement of the gradient impulse response function (GIRF) with a thin-slice method, In: Proceedings 27. Annual Meeting International Society for Magnetic Resonance in Medicine. Montreal, Canada, p. 0924.
[9] Vannesjo, Signe J., et al. "Gradient system characterization by impulse response measurements with a dynamic field camera." Magnetic resonance in medicine 69.2 (2013): 583-593.
[10] Rahmer, Jürgen, et al. "Rapid acquisition of the 3D MRI gradient impulse response function using a simple phantom measurement." Magnetic resonance in medicine 82.6 (2019): 2146-2159.
[11] Duyn, Jeff H., et al. "Simple correction method for k-space trajectory deviations in MRI." Journal of Magnetic Resonance 132.1 (1998): 150-153.
[12] Ruschke, Stefan, et al. "Correction of phase errors in quantitative water–fat imaging using a monopolar time‐interleaved multi‐echo gradient echo sequence." Magnetic resonance in medicine 78.3 (2017): 984-996.
[13] Mazurkewitz P, Rahmer J, Börnert P., GIRF measurement using a combination of triangular and chirp waveform input functions. In: Proceedings Joint Annual Meeting ISMRM-ESMRMB, Paris, France (2018).
Figures