Purpose

Signals with multiple exponential decays are often encountered in science and engineering. In MR field, T₁ and T₂ relaxation times is included. In many cases, we acquire MR signals which contain multiple T₂ components in a single voxel. There are previous attempts to decompose multiple-exponential decays without assuming the number of decays a priori such as using the inverse Laplace transform ^1-2 or linear optimization methods.^3-5 However, they are sensitive to ill conditions and have a poor resolving. In this study, we propose a new method that can analyze multiple exponential decays like T₂ decays with high resolution using the inverse Z-transform. It was demonstrated in simulation and in vivo human brain experiment, providing T₂-selective images and using them for myelin-water fraction mapping and deep brain-tissue segmentation.

Methods

Theory: The rationale for using the inverse Laplace transform (L^-1) originally comes from L^-1{exp(-snT)} = δ(t-nT), where T is a sampling interval in t-domain and n is a discrete sampling index. For applying the Z-transform, z can be defined as z_k = exp(s_kT): L^-1(z_k^-n) = δ(t-nT), where k is an integer from 0 to M-1 (M is a given integer). Therefore, it should be noted that, during the following discussion, acquired MRI signals belong to the s-domain, NOT to the t-domain. Assuming that there is a finite and discrete function, g(t), in t-domain, then

g(t) = Σ^N_n=1 x_n δ(t-nT) [1]

L{g(t)} = L{Σ^N_n=1 x_n δ(t-nT)} = Σ^N_n=1 x_n exp(-snT) [2]

= Σ^N_n=1 x_n z^-n = Z(g(t)) [3]

Eq.[2] and [3] show that a sum of T₂ exponential decays can be transformed to g(t), the sum of δ functions, using the inverse Z-transform. Since z = exp(s_kT), z can be redefined as AW^k (Fig. 1), where A = A₀exp(jθ₀) and W = W₀exp(jφ₀), θ₀ and φ₀ are the initial angles of A and W, decided arbitrarily.⁶ Then we can rewrite Eq.[3] in form of column vectors (X = [X_k], length M and x = [x_n], length N) and a coefficient matrix (C = [(AW^k)ⁿ]):

X = Cx [4]

The final results we want, i.e., the decomposed multi-component exponential decays, are the components of x, which is given by x = C^-1X (M = N). Components of x indicate which T2 decays are contained in the acquired MR signal, X.
Simulation: To test the effect of the inverse Z-transform in simulation, we built a synthetic phantom in MATLAB containing four different exponential decays with different R₂(=1/T₂)[1/ms] and amplitudes (Fig. 2A): 1000×exp(-0.046t), 3600×exp(-0.032t), 7500×exp(-0.02t), and 2000×exp(-0.01t), with 3% random noises. Both the first TE and ΔTE were assumed to be 10 ms, with 30 sample points. If the inverse Z-transform is working properly, it is expected that each exponential decay is separately displayed with the estimated R₂ values and magnitudes.
Human brain Experiment: Human brain experiment was also performed in the Siemens 3T Prisma system not only to test the proposed method itself, but also to explore some promising applications. A multi-echo GRASE sequence was used to obtain the myelin-water fraction(MWF) maps for reference. 40 slices were acquired and, for each slice, 32 echo images were acquired at varying TE from 10 to 320 ms by an increment of 10 ms. Scan parameters are given in Fig.4.

Results and Discussion

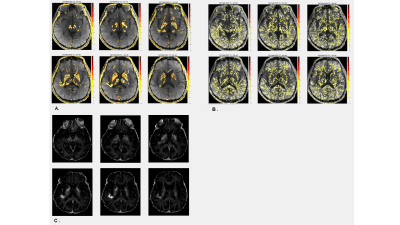
Figures 2B~E shows the R₂-selected images of the synthetic phantom, each of which corresponds to four components, respectively. Each exponential decay was successfully selected and displayed. The estimated amplitudes of each exponential decay across all the voxels in each T2-selected image were: 999.94±0.21(B), 2000.05±0.31(C), 3599.80±0.49(D), 7500.10±0.30(E), respectively, and the estimated R₂ values were: 0.045±0.007(B), 0.010±0.014(C), 0.033±0.007(D), 0.019±0.008(E). They were in excellent agreement with the original amplitudes and R₂ values.
Figure 3 shows T₂-selective human brain images (A, B) and MWF maps obtained from multi-echo GRASE for reference (C). Two T₂ ranges were selected by the proposed method, that is, 45~55 ms(A) and 55~65 ms(B), respectively. It is interesting that the shorter T₂-selective images (A) seem to separate deep brain structures such as thalamus (arrow 1), putamen and globus pallidus (arrow 2), whereas the longer T₂-selective images (B) seem to represent the MWF maps except for the deep brain structures shown in Fig. 3A. A combination of Figs. 3A and B looks like the actual MWF maps, which are good agreement with Fig. 3C.

Conclusion

In this study, we proposed a method that effectively decomposes the relaxation-time decays, e.g., T₂ decays, using the inverse Z-transform. The method can be easily applied to T₁ decays. Its performance was successfully demonstrated in simulation and in vivo human brain experiment. The proposed method can provide T₂-selective imaging with T₂ ranges what we want. In addition, when compared to the previous works using the inverse Laplace transform ^1,2 or a linear inversion program ^4,5, it is less sensitive to ill-posed problems and provide highly T₂-resolved images. It is also expected to find uses in many interesting applications such as MWF mapping and accurate segmentation of brain tissue including subcortical gray matters etc. A further study is warranted for investigating the maximum T₂ range that can be resolved, the highest T₂ resolution that can be achieved, and the relationship between T₂ range and T₂ resolution.

Acknowledgements

This work was supported by SMC-SKKU Future Convergence Technology Program.