3368
Sensitivities Constrained Phase Update (sCPU) for Ghost Artifacts Reduction
Hai Luo1, Meining Chen1, Ziyue Wu2, Bei Lv1, Fei Peng1, Shijie Wang1, Wenkui Hou1, Weiqian Wang1, and Gaojie Zhu1
1AllTech Medical Systems, Chengdu, China, 2Marvel Stone Healthcare, Wuxi, China
1AllTech Medical Systems, Chengdu, China, 2Marvel Stone Healthcare, Wuxi, China
Synopsis
Compared with magnitude value, phase of MRI signal is more prone to be influenced by motion. A novel method, sensitivity constrained phase update (sCPU) was proposed for robust and efficient ghost artifacts reduction. Using coil sensitivities as constraints, a synthetic image can be generated in which the ghost is reduced due to phase cancelation. Phase error was first estimated from the raw image and the synthetic image, and then was used to update the phase of raw k-space. The results with simulated and in-vivo data show that the ghost artifacts can be efficiently reduced after several iterations.
Introduction
Many techniques have been designed to compensate for pseudo-periodic1-4 and rigid-body motion5. Some of these techniques need to oversample the K-space data to estimate motion, such as PROPELLER4,5. Another kind of retrospective techniques compensate the motion in K-space, such as COCOA6 and PANDA7. Empirical thresholds are used in these techniques to identify the corrupted data, which are hard to be optimized for different clinical cases. Moreover, although these techniques are effective against random or sudden movement, they are ineffective when there is strong coherence of the ghost (Eg: rigid translation). Here a novel, sensitivity constrained phase update method, is proposed for the reduction of different kinds of ghost artifacts. Compared with magnitude value, phase of MRI signal is more prone to be influenced by motion. So once the phase error is corrected, the ghost artifacts can be largely suppressed.Method
For each individual coil image at position $$$y$$$, ghost artifacts were modulated by sensitivities, it could be written as $$m_i(y)=S_i(y)m_i(y)+\sum_{p=1}^{P}\omega_pS_i(y+\Delta y_p)m_k(y+\Delta y_p)\qquad(1)$$Here $$$S_i$$$ is the sensitivity, $$$y+∆y_p$$$ represents where the folded artifacts is come from and totally $$$P$$$ folded positions. $$$ω_p$$$ is the ghost level.Using sensitivities as a constraint, a synthetic image can be generated via equation (2) $$synm_i(y)=S_i(y)\frac{\sum_{j,k}S_{j}^{*}(y)\psi_{j,k}m_k(y)}{\sum_{j,k}S_{j}^{*}(y)\psi_{j,k}S_k(y)} \qquad(2)$$ $$$ψ_(j,k)$$$is the noise correlation, combining equations (1) and (2),$$synm_i(y)=S_i(y)m_i(y)+S_i(y)\frac{\sum_{j,k}S_{j}^{*}(y)\psi_{j,k}[\sum_{p=1}^{P}\omega_pS_k(y+\Delta y_p)m_k(y+\Delta y_p)]}{\sum_{j,k}S_{j}^{*}(y)\psi_{j,k}S_k(y)} $$$$=S_i(y)m_i(y)+S_i(y)\sum_{p=1}^{P}\omega_p{\chi} m_{k}(y+\Delta y_p) \qquad(3)$$
where$$\chi=\frac{\sum_{j,k}S_{j}^{*}(y)\psi_{j,k}S_k(y+\Delta y_p)}{\sum_{j,k}S_{j}^{*}(y)\psi_{j,k}S_k(y)}$$
For phase array coils, sensitivity is spatially varied that means $$$S_j (y)$$$ and $$$S_k (y+∆y_p )$$$ have different phase and magnitude. $$$\chi$$$ is much less than 1 due to high probability of phase cancellation. So, the ghost component in synthetic image is smaller while the true image component remains unchanged, as in Fig 1.
Fourier Transform of the difference of raw and synthetic image into frequency domain, we can get the phase error$$\Delta \varphi_i=\phi (F(m_i-synm_i)) \qquad(4)$$Where $$$F$$$ is the Fourier Transform operator and $$$ϕ$$$ is a phase operator. To control the noise amplification during the phase update, a magnitude weighted phase combination of all coils was performed. $$\Delta \varphi=\sum_{i}^{N}\lambda_i\Delta \varphi_i \qquad(5)$$Finally, phase error $$$\Delta \varphi$$$ can be subtracted from the raw k-space to reduce the ghost artifact, the iterative update approach could be written as$$ K_{n+1}=K_ne^{-i\Delta \varphi}\qquad(6)$$
Simulated and in-vivo data was used to validate the proposed method. A standard head image and 8ch sensitivities (http://hansenms.github.io/sunrise/sunrise2013/) were used for simulation, with both linear and random phase error to simulate motion induced artifacts. Also Gaussian noise was simulated to verify the degradation due to noise.
Two in-vivo datasets, head T2 FSE images and abdominal triggered T2 FSE images, were acquired on a 1.5T whole-body scanner (Centauri, Alltech Medical Systems). For head imaging, acquisition parameters were ETL 16, FOV 230mmx230mm, TR/TE 5000/90ms, matrix size 256*256 and 8 channel head coil. There were two intentional slight head shakes during the scan. For abdominal imaging, acquisition parameters were ETL 16, FOV 300mmx350mm, TR/TE 3672/90ms, matrix size 240*256, 15 channel torso coil. Since the volunteer’s breathing was very bad, there were obvious ghost artifacts. The sensitivity maps were calibrated via ESPIRiT8 with 6x6 kernel from 24 calibration lines.
Results
Fig. 2 shows the ghost reduction results with simulated data. Fig.2a & Fig.2d are the simulated ghost images with linear and random phase error respectively. Fig.2b & Fig.2e are the correction results and Fig.2c & Fig.2f are the ghost map. The ghost artifact had almost been cleared in 10 iterations, but a little noise amplification is seen.Fig. 3 shows convergence performance and noise amplification during the iterations. The algorithm converges very fast that the residual ghost is very small after 5~10 iterations while the noise amplification increases slowly with iteration. From this simulation, 5~10 iteration is a good compromise between ghost reduction and noise amplification.
Fig.4&Fig.5 are the in-vivo application of the proposed method. The results show that the ghost due to head shake or irregular breathing had been dramatically reduced.
The computing time per 256x256 image for 10 iteration is about 500ms, using MATLAB on a PC with Intel i7@3.6GHz and 16G RAM.
Disscussion
Advantages: First of all, the proposed method does not require extra hardware or additional data. Second, both Cartesian and non-Cartesian acquisition are applicable. Third, this method is fast and robust, ghost due to periodic or random motion can be efficiently reduced.Sensitivity map: Accurate and fast varying receiver sensitivity map is the critical factor for estimating the phase error. Since phase array coils were optimized for parallel imaging, the sensitivity often varies fast. From our test results, sensitivity map via ESPIRiT calibration is accurate enough in most cases.
Noise amplification: There was a bit more noise amplification for large number iteration. From the simulation, 5~10 iteration is a good compromise between ghost reduction and noise amplification. Filtering or fitting the phase error can be implemented as a further work to control the noise amplification.
Conclusion
A novel method, named sCPU, was proposed for robust and efficent ghost reduction. Motion induced error was estimated from the raw image and a sensitivity constrained synthetic image, then it was subtracted from the raw k-space to iteratively reduce ghost artifact. The results with simulated and in-vivo datasets show that the ghost artifacts can be efficiently reduced after several iterations.(Code: https://github.com/concher009/MRI/tree/master/sCPU )
Acknowledgements
No acknowledgement found.References
- Van A T, Hernando D, Sutton B P. Motion-induced phase error estimation and correction in 3D diffusion tensor imaging[J]. IEEE transactions on medical imaging, 2011, 30(11): 1933-1940.
- Bailes D R, Gilderdale D J, Bydder G M, et al. Respiratory ordered phase encoding (ROPE): a method for reducing respiratory motion artefacts in MR imaging[J]. J Comput Assist Tomogr, 1985, 9(4): 835-838.
- Larson A C, White R D, Laub G, et al. Self‐gated cardiac cine MRI[J]. Magnetic Resonance in Medicine: An Official Journal of the International Society for Magnetic Resonance in Medicine, 2004, 51(1): 93-102.
- Pipe J G. Motion correction with PROPELLER MRI: application to head motion and free‐breathing cardiac imaging[J]. Magnetic Resonance in Medicine: An Official Journal of the International Society for Magnetic Resonance in Medicine, 1999, 42(5): 963-969.
- Hai Luo, Gaojie Zhu, Xiang Zhou , et al. Improved non-rigid motion suppression for free-breathing PROPELLER with adaptively weighted blade combination. In Proceedings of the 26th Annual Meeting of ISMRM, Paris, 2018.
- Huang F, Lin W, Börnert P, et al. Data convolution and combination operation (COCOA) for motion ghost artifacts reduction[J]. Magnetic resonance in medicine, 2010, 64(1): 157-166.
- Gaojie Zhu , Xiang Zhou , Hai Luo, et al. Motion Artifacts Reduction by Parallel Acquisition with Non-prolonged Deghosting Algorithm (PANDA). In Proceedings of the 25th Annual Meeting of ISMRM, Hawaii, 2017, p.786.
- Uecker M, Lai P, Murphy M J, et al. ESPIRiT—an eigenvalue approach to autocalibrating parallel MRI: where SENSE meets GRAPPA[J]. Magnetic resonance in medicine, 2014, 71(3): 990-1001.
Figures
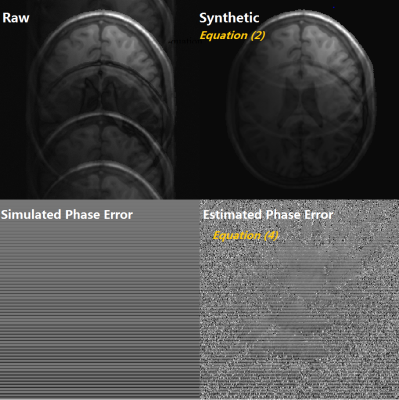
Fig 1. The top left is a raw ghost image and the top
right is the sensitivity constrained synthetic image via equation (2) in first
iteration. There is obviously less ghost in the synthetic image. Fourier
Transform of the difference of the raw and synthetic image into frequency
domain, the
phase error can be estimated. It is used to update the raw K-space phase for
ghost reduction. After several phase update iterations, the estimated phase
error gradually approaches the simulated phase error.
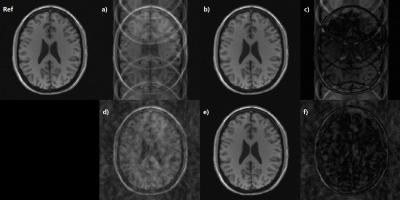
Fig2. Ghost reduction simulation.
a&d) Simulated ghost images with linear phase error and random phase error,
b&e) Correction results after 10 iterations, c) Ghost map[a – b], f) Ghost
map[d – e]. The ghost artifact had almost been cleared but a little noise amplification
is seen.
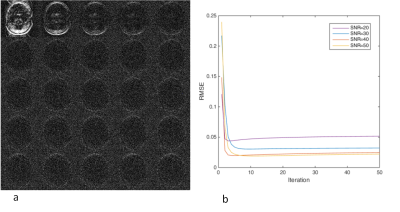
Fig 3. Validation
of the algorithm convergence and noise amplification. A simulated dataset with
linear phase error ghost was used. a) Residual artifact of 1~25 iterations (with
30dB Gaussian noise), b) Root Mean Square Error on different noise level. The
residual artifact is very small after 5~10 iterations while the noise
amplification increases slowly with iteration. The
better SNR, the less residual error and less noise amplification. From this simulation,
5~10 iteration is a good compromise between ghost reduction and noise
amplification.
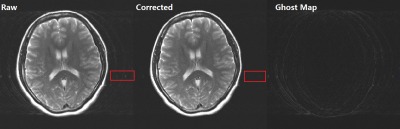
Fig 4. Application to reduce head
shake ghost artifacts. T2 FSE, ETL=16, 8ch phase array coils, sensitivity maps
were calibrated via ESPIRiT form 24 central lines. The middle is the correction
result after 10 iterations and the right one is (Raw – Corrected). Ghost due
to head shake was dramatically reduced, also pulsation artifacts were partially
suppressed as indicated by the red rectangles. The noise amplification is not
obvious.
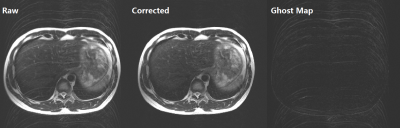
Fig 5. Application to reduce
ghost artifact due to irregular
breathing. Respiratory triggered T2 FSE,
ETL=16, 15ch phase array coils, sensitivity maps were calibrated via ESPIRiT
form 24 central lines. The middle is the correction result after 10 iterations
and the right one is (Raw – Corrected). Ghost due
to irregular breathing was dramatically reduced,
but a little noise amplification.