3366
Towards Optimal Design of Orbital K-Space Navigators for 3D Rigid-Body Motion Estimation1Institute for Biomedical Engineering, ETH Zurich and University of Zurich, Zurich, Switzerland
Synopsis
A single-shot k-space navigator trajectory and a corresponding motion estimation algorithm is proposed. They allow for 3D rigid-body motion estimation. Their performance in terms of accuracy and precision is studied and a cross-validation experiment is conducted to show that the method is suitable for in-vivo use. The accuracy and precision of the method depend on the orbital radius of the navigator. A simulation study is conducted to determine the best choice of the navigator radius.
Introduction
Artifacts due to patient motion are a frequent problem in MR imaging practice. K-space navigators can correct for patient motion without requiring any additional hardware, and are thus promising for a wide range of applications. Single-shot navigators can be played out very quickly and may be incorporated in many MR sequences. A promising approach are orbital navigators, but they have originally been proposed for 2D rigid-body motion estimation. Moreover, it is unclear which orbital radius yields the best accuracy and precision, because with increasing radius, the number of features in the k-space signal increases, but the signal-to-noise ratio decreases. In this work, a 3D single-shot version of orbital navigators is proposed, which allows for 3D rigid-body motion estimation. Moreover, the influence of the radius on accuracy and precision is studied.Methods
An orbital navigator (ONAV) can detect rotations and translations in a two-dimensional plane.1 To detect 3D rigid-body motion, three orthogonal ONAVs are necessary. It has been proposed to acquire and process the three ONAVs separately with a readout duration of 5.6 ms each.2 To shorten the navigator acquisition duration, we propose a single-shot trajectory, whose shape resembles a sequence of three orthogonal ONAVs. To further speed up the acquisition, without exceeding the gradient strength and slew rate limit, smooth transition segments were inserted between the ONAVs. It has previously been shown3 that trajectory errors negatively affect the accuracy of navigator-based motion estimation. Therefore, the field evolution was monitored4 to measure the actual trajectories and account for any gradient encoding inaccuracy during data processing.To deal with simultaneous rotations around all three coordinate axes, it is necessary to acquire some reference data around the single-shot trajectory once at the beginning of the scan (Fig. 1). During the actual scan, only a single-shot navigator needs to be acquired and compared to the reference signal as detailed below.
Rotations of the imaging object induce the same rotation of the signal in Fourier space, while translations of the object lead to linear phase shifts of the Fourier signal. Therefore, we follow a two-step approach by first
- calculating the rotation angles by iterative least-squares minimization using the magnitude of the navigator signal, and then $$\Vert\vert s_{mov}\vert - rot(\vert s_{ref}\vert,\theta) \Vert_2^2 \rightarrow \min_{\theta}\qquad(1)$$
- calculating the translation vector from the phase of the navigator signal using weighted least-squares minimization. $$\Vert W\cdot (\Delta\varphi - k^T \Delta x) \Vert_2^2 \rightarrow \min_{\Delta x}\qquad(2)$$
Here, $$$s_{ref}$$$ and $$$s_{mov}$$$ denote the k-space navigator signal measured before and after patient movement, respectively. Moreover, $$$\Delta\varphi=arg(s_{mov})-arg(s_{ref})$$$ denotes the phase difference between the navigator signals. Since the phase signal has the highest SNR at samples with large magnitude, the samples are weighted by the diagonal matrix $$$W$$$, whose entries are the signal magnitudes. Calculating $$$rot(\vert s_{ref}\vert,\theta)$$$, i.e., the reference signal rotated along a set of Euler angles $$$\theta$$$ requires regridding/interpolation of the k-space navigator signal, which is performed by convex combination of nearby signal values $$$s_n$$$. The relative weights are given by a Kaiser-Bessel kernel (denoted by $$$\mathcal{K}$$$) and a density correction factor $$$D_n$$$, which adjusts interpolation weights according to the local sampling density.
$$ s(k) = \frac{\sum_{n=0}^N \mathcal{K}(k-k_n) D_n s_n}{\sum_{n=0}^N \mathcal{K}(k-k_n)D_n} $$
Since the minimization problem$$$\,(1)\,$$$is locally convex and differentiable, it was solved with a trust-region algorithm.5
Experiments
The accuracy and precision of our method was estimated from a simulation study using a 3D brain phantom. For randomly chosen Euler angles $$$\theta\in[-6°,6°]^3$$$ and translation vectors $$$t\in[-2mm,2mm]^3$$$, the corresponding k-space signal was calculated along the reference trajectory before the transformation, and along the one-shot trajectory after the transformation. Then, the motion parameters were estimated using the proposed algorithm.
Accuracy was evaluated for$$$\,N=32\,$$$sets of random rotation angles and shift vectors. Precision was evaluated with$$$\,N=32\,$$$instances of zero-mean iid Gaussian noise on the k-space signal. The noise variance was chosen so that the k-space noise was equivalent to Gaussian noise in image space with $$$SNR=10$$$.
Additionally, to demonstrate that our method is suitable for in-vivo motion correction, a cross-validation experiment of the proposed method with 3D image registration was performed. After acquiring a navigator signal and a 3D T1-weighted TFE image, the volunteer was instructed to perform a nodding motion. Afterwards, another navigator and TFE image were acquired. Motion parameters were estimated independently by our navigator method, and by image registration.
Results
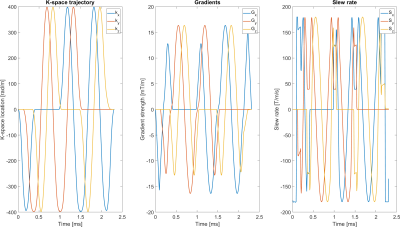
The highest accuracy and precision is achieved for radii in the range of $$$r\in[300,400]\,rad/m$$$ (Fig. 3,4). For a radius in this range, the navigator can be played out in less than 2.5 ms (Fig. 2) with a maximum slew rate of 180 mT/m/s and a maximum gradient strength well below 20 mT/m.Our imaging experiment shows good agreement of the motion values estimated using image registration and our proposed method (Fig. 5), indicating that the motion parameters from the navigators were estimated correctly.
Discussion/Conclusion
We have proposed a fast single-shot navigator trajectory and a corresponding motion estimation algorithm. The navigator was optimized to achieve best performance in terms of accuracy and precision, which was achieved at an orbital radius of 300 to 400 rad/m. A cross-validation experiment with image registration indicated that motion was correctly estimated in vivo. A more detailed analysis of the performance is to be conducted soon.Acknowledgements
No acknowledgement found.References
- Fu Zhuo Wu et al. Orbital navigator echoes for motion measurements in magnetic resonance imaging. Magnetic Resonance in Medicine 34, 746–753 (1995).
- Ward Heidi A. et al. Prospective multiaxial motion correction for fMRI. Magnetic Resonance in Medicine 43, 459–469 (2000).
- Ulrich, T., Patzig, F., Wilm, B. J. & Pruessmann, K. P. 3D Rigid-Body Motion Estimation for Brain Imaging using Orbital Navigators and Field Monitoring. ESMRMB 2019.
- Barmet, C., Zanche, N. D. & Pruessmann, K. P. Spatiotemporal magnetic field monitoring for MR. Magnetic Resonance in Medicine 60, 187–197 (2008).
- Coleman, T. & Li, Y. An Interior Trust Region Approach for Nonlinear Minimization Subject to Bounds. SIAM J. Optim. 6, 418–445 (1996).
Figures
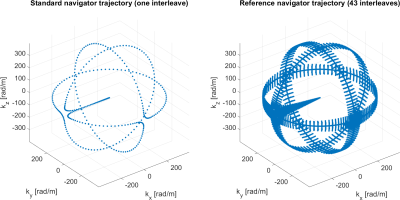
Left: K-space navigator trajectory. Note that all sharp turns between orthogonal circles have been replaced with smooth transitions. Right: Reference acquisition, consisting of 43 interleaves. In every interleave, the trajectory is rotated around one of the coordinate axes by a different angle $$$\varphi\in[-7,7°]$$$. This interval corresponds to the range of rotations, which the navigator can detect. If larger patient motion is expected, larger angles can be chosen for the rotated interleaves.
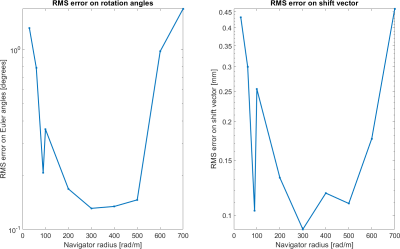
Accuracy of motion estimation in the simulation experiment. Left: RMS error on rotation angles. Right: RMS error on shift vector.
The best accuracy of 0.1307° and 0.09mm is attained for a navigator radius of r=300 rad/m. The U-shape of the curve is expected, because, firstly, for small radii, the k-space navigator signal does not contain as many distinct features, which are necessary for registering two navigator signals to each other. Secondly, for large radii, the signal-to-noise ratio of the signal decreases.
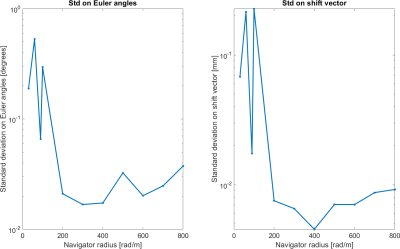
Precision of motion estimation in the simulation experiment. Left: Standard deviation of rotation angles. Right: Standard deviation of shift vector.The best precision value of 0.0168° for rotation angles is attained at r=300 rad/m, while the best precision value of 0.0046mm for the translation vector is attained at r=400 rad/m.
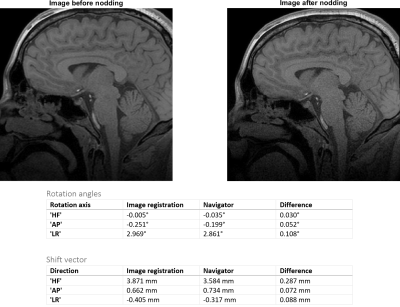
Upper row: One slice of the sagittal images used for image registration, before and after instructed nodding motion. Lower row: Table with rotation angles and shift vector estimated by the navigator method and image registration, respectively. The values are in good agreement, which indicates that the navigator method is estimating the motion correctly.