3361

Modelling RF coil-sensitivity induced artefacts in prospective motion-corrected accelerated 3D-EPI fMRI
Nadine N Graedel1, Yael Balbastre1, Nadège Corbin1, Oliver Josephs1, and Martina F Callaghan1
1Wellcome Centre for Human Neuroimaging, UCL Queen Square Institute of Neurology, University College London, London, United Kingdom

Synopsis

The increased SNR offered by 3D EPI makes it well-suited for high-resolution fMRI but this benefit needs to be weighed against the increased motion sensitivity. Even when prospective motion correction is used to create a consistent excitation volume and image encoding, residual artefacts remain, caused for example by the apparent motion of coil sensitivities relative to the head after PMC. Using simulated fMRI data we examined the impact of this effect on fMRI and a potential correction using motion-adjusted GRAPPA calibration combined with volume-wise bias field removal which in simulations achieved improved sensitivity and specificity of detection of activation.

Introduction

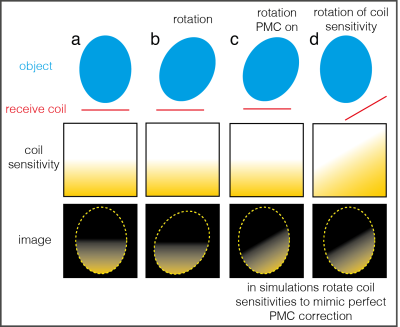
The capacity to under-sample in the second phase-encoded direction makes 3D-EPI attractive for high-resolution fMRI1. However, 3D-EPI is also more vulnerable to subject motion due to its multi-shot nature. Prospective motion correction2-4 (PMC) allows image encoding errors and spin-history effects to be corrected by adjusting the excitation volume and the encoding gradients to track the imaging volume. However a number of motion-related artefacts remain even after perfect PMC5-6. Here we focus on those caused by apparent motion of the stationary receiver coils relative to the participant, in the context of fMRI (see Figure 1). The apparent movement of the coil sensitivities creates two problems in accelerated 3D-EPI fMRI:
  1. Each volume has a different spatial modulation as a result of the changing coil sensitivities (inter and intra-volume). If each individual image is motion-free (reasonable assumption for 2D imaging) and accurate coil sensitivities are available this can be corrected with a motion-adjusted Roemer-optimal coil combination7. More generally volume-wise sensitivity modulation can be estimated and removed in post-processing8.
  2. Artefacts arise during reconstruction due to inconsistencies between reference data9, typically acquired at the start of the time series, and the data to be reconstructed.
Artefacts 1 and 2 can be addressed by combining augmented SENSE10 with motion-adjusted coil sensitivities11-13 if sensitivities combine to form an effectively unmodulated image, e.g. when determined relative to a body coil rather than sum-of-squares reference.
In this work we instead aim to correct these artefacts by (i) calibrating separate GRAPPA14 kernels with motion-compensated reference data for each partition and (ii) removing residual sensitivity modulation in post-processing. The proposed approach has the advantages of a simple/non-iterative image reconstruction and less stringent requirements on the reference data, which could be useful at 7T where a body coil reference is generally not available.

Methods

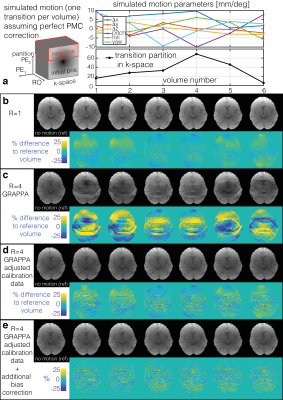
Task fMRI data (50 volumes) were simulated to mimic the case of perfect PMC by moving complex coil sensitivities (from a 32channel coil at 3T, fitted to obtain sensitivities over the full FOV15) relative to a stationary complex baseline image. One large step motion was simulated to occur during each fMRI volume (randomly sampled from rotations[pitch/roll/yaw] = +/-[10/10/15] degrees and translations[Δx/Δy/Δz] = +/-[10/5/5] mm) at a random partition in 3D k-space. Thermal noise (using measured noise covariance between coils) was added to the real and imaginary channels of each coil to give an approximate tSNR of 50. Finally, a 4 % signal increase was added for grey matter voxels of the visual cortex following a block design of 5 volumes ON/OFF. The data were under-sampled in the PE direction (R=4) and reconstructed with GRAPPA using either:
  1. Motion-free start volume as reference data for GRAPPA calibration.
  2. Motion-adjusted reference data accounting for the apparent movement of the coil within and between volumes.
In an additional step, the final time series (sum-of-squares across coils) were modelled as one common image modulated by smooth, volume-specific net coil sensitivities15. This model was solved iteratively by optimising the joint log-likelihood of the log sensitivities and their Fréchet mean, taken to be the common image, which enforces smoothness by penalising bending energy. Only white matter and CSF voxels were used in the optimisation to avoid overfitting the sensitivities to activation-related fluctuations in grey matter. These estimated volume-specific modulations were subsequently removed from the time series.GLM-detected percent changes within (sensitivity) and outside (specificity) the activated ROI were compared to a non-motion-corrupted ground truth simulation.

Results

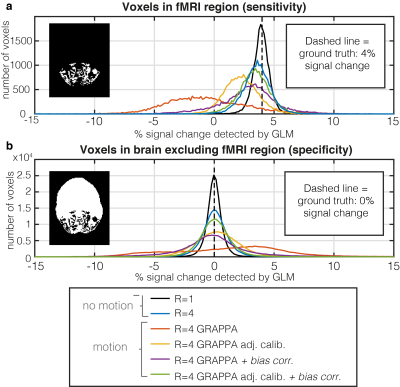
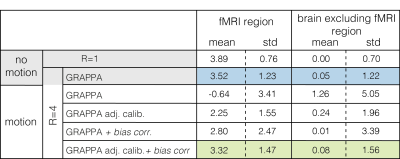
When uncompensated, acceleration in the presence of PMC-corrected motion leads to substantial GRAPPA-related artefacts (Fig.2c). These are largely removed by using motion-adjusted calibration data (Fig2d). This greatly improves the sensitivity and specificity to functional activation (Fig.3, Table 1). As in the unaccelerated case (data not shown), the fidelity of the identified activation is further improved by additionally compensating for residual volume-specific modulations, almost reaching levels observed in the no motion condition.

Discussion

The impact of motion-induced encoding inconsistencies when no/imperfect PMC is applied is much larger than that of apparent movement of coil sensitivities16. Nonetheless our simulations show that even after perfect PMC the effect of changing coil sensitivities can compromise fMRI analyses, especially when parallel imaging is used. The corrections we applied removed this effect to a large degree. Further testing is required to see if these findings can be replicated in-vivo where other imperfections (e.g. changing shim) are present, and where the required extrapolation of the sensitivities over the full FOV to generate motion-adjusted reference data will be more challenging. We will also assess the relative merits of this approach with more general SENSE-based iterative reconstructions10-13.
In this work we ignored position-dependent changes to the coil sensitivities caused by differential loading and wave effects, a reasonable simplification at 3T17. However at higher fields this may need to be incorporated to achieve a good correction.

Conclusion

If uncorrected the interaction between coil sensitivities and motion can cause artefacts and compromise fMRI studies, in terms of both sensitivity and specificity, when using 3D-EPI. In simulation, an adjusted GRAPPA reconstruction combined with removal of volume-specific residual modulations mitigates these artefacts to enable accurate detection of functional activation.

Acknowledgements

The Wellcome Centre for Human Neuroimaging is supported by core funding from the Wellcome [203147/Z/16/Z].

References

1: Poser, B A et al. “Three dimensional echo-planar imaging at 7 Tesla.” NeuroImage vol. 51,1 (2010): 261-6. doi:10.1016/j.neuroimage.2010.01.108

2: Thesen, S et al. “Prospective acquisition correction for head motion with image-based tracking for real-time fMRI.” Magnetic resonance in medicine vol 44,3 (2000): 457–465.

3: Zaitsev Maxim et al. “Magnetic resonance imaging of freely moving objects: prospective real-time motion correction using an external optical motion tracking system.” NeuroImage vol. 31,3 (2006):1038–1050.

4: Todd, Nick et al. “Prospective motion correction of 3D echo-planar imaging data for functional MRI using optical tracking.” NeuroImage vol. 113 (2015): 1-12. doi:10.1016/j.neuroimage.2015.03.013

5: Zaitsev, Maxim et al. “Prospective motion correction in functional MRI.” NeuroImage vol. 154 (2017): 33-42. doi:10.1016/j.neuroimage.2016.11.014

6: Zaitsev, Maxim et al. “Motion artifacts in MRI: A complex problem with many partial solutions.” Journal of magnetic resonance imaging : JMRI vol. 42,4 (2015): 887-901. doi:10.1002/jmri.24850

7: Faraji-Dana, Zahra et al. “A robust method for suppressing motion-induced coil sensitivity variations during prospective correction of head motion in fMRI.” Magnetic resonance in medicine vol 34,8 (2016): 1206–1219. doi: 10.1016/j.mri.2016.06.005

8: Seshamani, Sharmishtaa et al. “A method for handling intensity inhomogenieties in fMRI sequences of moving anatomy of the early developing brain.” Medical image analysis vol. 18,2 (2014): 285-300. doi:10.1016/j.media.2013.10.011

9: Faraji-Dana, Zahra et al. “Interactions between head motion and coil sensitivity in accelerated fMRI.” J Neurosci Methods vol 270 (2016): 46–60. doi: 10.1016/j.jneumeth.2016.06.005

10: Bammer, Roland et al. “Augmented generalized SENSE reconstruction to correct for rigid body motion.” Magnetic resonance in medicine vol. 57,1 (2007): 90-102. doi:10.1002/mrm.21106

11: Yarach, Uten et al. “The correction of motion-induced coil sensitivity miscalibration in parallel imaging with prospective motion correction.” Proc. Intl. Soc. Mag. Reson. Med. 23 (2015) p. 2558

12: Yarach, Uten et al. “Correction of B0-induced geometric distortion variations in prospective motion correction for 7T MRI.” Magma vol. 29,3 (2016): 319-32. doi:10.1007/s10334-015-0515-2

13: Herbst, M et al. “Motion correction for diffusion weighted SMS imaging.” Magnetic resonance imaging vol. 38 (2017): 33-38. doi:10.1016/j.mri.2016.12.013

14: Griswold M et al. “Generalized autocalibrating partially parallel acquisitions (GRAPPA).” Magnetic Resonance in Medicine vol. 47,6 (2002): 1202–1210. doi: 10.1002/mrm.10171

15: Balbastre, Yael et al. “A Generative Approach to Estimating Coil Sensitivities from Autocalibration data” Proc. Intl. Soc. Mag. Reson. Med. 27 (2019) p. 4762

16: Graedel N et al. “Investigation of the impact of receive field sensitivity on motion corruption in 3D-EPI for fMRI” Proc. Intl. Soc. Mag. Reson. Med. 27 (2019) p. 4439

17: Tian Qiyuan et al. “Effects of Motion on Coupling of Coil Elements and Parallel Imaging Reconstruction at 3T and 7T” Proc. Intl. Soc. Mag. Reson. Med. 23 (2015) p. 2419

Figures

Fig. 1: Interaction of motion, coil sensitivities and prospective motion correction: When no PMC is used (b) the object moves in the FOV but the coil sensitivities remain valid with respect to the FOV coordinate space (when ignoring the impact of motion on coil loading). The adjustment of the FOV to account for object motion in the PMC case (c) cause the coil sensitivities to apparently move within the FOV coordinate space relative to the now stationary object. This effect can be recreated in simulations by moving the coil sensitivities relative to the head (d).

Fig. 2: Motion simulations assuming perfect PMC (coil sensitivities moving only). Step motions and transition partitions are given for 6 volumes in (a). Images and differences to a non-motion corrupted reference show impact of moving sensitivities for R=1(b) and R=4(c-e) data. GRAPPA kernels were calibrated on the reference data set (c) or motion-adjusted reference data (d/e). In (e) additional bias field correction was performed in post-processing. Volumes 3-6 are in a task ON block (activation visible in e).

Fig. 3: Results of GLM analysis of the simulated fMRI time series: Detected percent changes within (a) and outside (b) the activated ROI provide metrics for the sensitivity and specificity. The motion simulations were compared to a non-motion-corrupted ground truth simulation.

Fig. 4: Table containing quantitative results from the fMRI analysis shown in figure 3: Mean and the standard deviation of the percent change of all voxel within (sensitivity) and outside (specificity) the activated ROI.

Proc. Intl. Soc. Mag. Reson. Med. 28 (2020)
3361