Synopsis

Multi-contrast-based parametric MRI techniques provide parametric maps intrinsically sensitive to voxel misalignment upon images combination.

In this work, we propose an efficient retrospective motion correction method adapted to this problem, with an application to inhomogeneous Magnetization Transfer (ihMT) imaging. The proposed method is confronted with the MCFLIRT (FSL) method used as reference, and residual motion is quantified and analysed across native and motion corrected images.

Introduction

Parametric images based on the combination of MRI images with varying contrasts for composite map generation, such as inhomogeneous Magnetization Transfer (ihMT), are of great interest for structural evaluations in the central nervous system^1,2. However, potential voxels misalignment across acquired images, induced for instance by subject motion, may result in inconsistencies in the computed maps (loss of sharpness or localized artifacts), which bias further analyses. Compensation schemes to account for images misalignment must thus be considered.

In this work, we propose an efficient and robust retrospective motion correction framework for multi-contrast-based imaging techniques (MC-MoCo) accounting for a limited number of available images as specific feature. The proposed method was applied on 3D ihMT images acquired with a clinical routine procedure³ on healthy subjects and Multiple Sclerosis (MS) patients. The MC-MoCo method was compared to MCFLIRT⁴, available in the FSL package, and showed higher performances for motion correction for both populations.

Materials and methods

Imaging experiments were performed at 1.5T (Avanto, Siemens, Erlangen, Germany) using a sensitivity-enhanced 3D ihMT-GRE³ sequence on 6 healthy volunteers and 7 patients with relapsing-remitting MS.

Thirteen 3D images were sequentially acquired and consisted on a reference volume (MT0, no radiofrequency saturation prior to image acquisition), followed by three repetitions of 4 different frequency-offset (Δf) MT-weighted (MTw) volumes (MT+ (Δf=+8 kHz), MT+- (Δf=+/-8 kHz), MT- (Δf=-8 kHz) and MT-+ (Δf=-/+8 kHz))³.

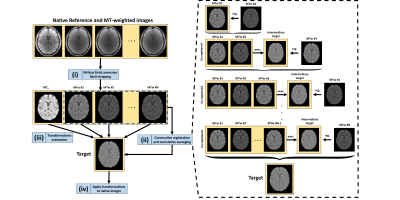
Figure 1 illustrates the MC-MoCo method. The whole process, which relies on functionalities provided in the ANTs registration package⁵, can be summed up as follows: (i) N4 bias-field correction⁶ and template-based skull-stripping of the native volumes, (ii) target building based of the MTw images, (iii) registration of each native skull-stripped volumes onto the target, (iv) application of the estimated transformations to each native volume. The MC-MoCo method was compared to MCFLIRT⁴ using the averaging option for target building in order to avoid the bias associated to the target choice among the various available contrasts in the case of a single available target option. Both MC-MoCo and MCFLIRT methods exclusively utilized rigid-body transformations and the mutual information metric⁷ to account for the various contrasts.

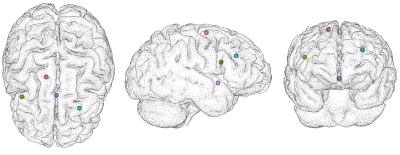
Residual motion following the application of motion correction methods was used to evaluate the efficiency of MC-MoCo and MCFLIRT. For that, landmarks were positioned over each native and motion-corrected volume at specific anatomical regions depicted in Figure 2, using 3D Slicer⁸. For each image group (uncorrected, MCFLIRT, and MC-MoCo), each subject and each marker, the barycentre of the respective locations on every volume was computed to serve as a reference point for the estimation of the residual movement. This metric, defined as the mean distance to the barycentre over every volume, quantifies the efficiency of a motion correction method for a single marker and a single subject: more efficient methods will yield lower residual motion.

Statistical analyses were performed to test for the significance of MC-MoCo and MCFLIRT on correcting motion and to ensure that both methods performed similarly for each marker and each subject group (control or MS); we hence estimated a mixed-effects linear model, with fixed effects on the motion correction method, the marker, and the subject group, and with a random effect on the subject, added to account for the non-independence of the observations within a subject.

Results

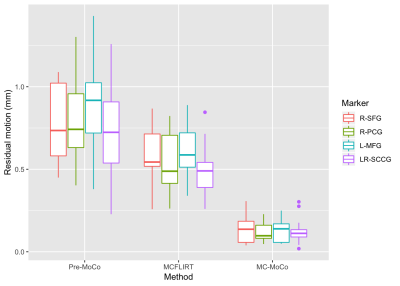
A boxplot of the residual motion grouped before and after corrections is shown in Figure 3: this plot indicates that MC-MoCo has less residual motion than MCFLIRT and that this behavior is rather constant across all markers.

The ANOVA on the estimated model shows a significant effect of the motion-correction method (p<0.01), but no significant effect of the marker (p=0.14) or of the group of the subject (p=0.12). Post-hoc tests, with p-values corrected for multiple comparison, show that residual motion is significantly reduced with respect to the non-corrected images by both MCFLIRT (-0.43 mm, p<0.01) and MC-MoCo (-0.68 mm, p<0.01), and that MC-MoCo significantly outperforms MCFLIRT (p<0.01). Both MC-MoCo and MCFLIRT performed similarly for controls and MS patients (no significant group effect, p>0.05).

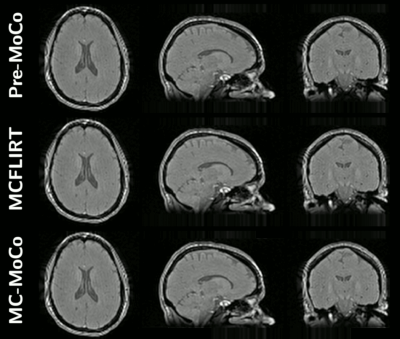
Representative animated MT0 and MTw images in orthogonal views for one subject before and after motion corrections are provided in Figure 4. Figure 5 shows representative ihMT images in orthogonal views, depicting the removal of artifacts relative to misalignment correction when using MCFLIRT and MC-MoCo.

Discussion and conclusion

The key point of the MC-MoCo method lies in the target building step. As opposed to other motion-correction methods based either on an averaged target over all native images or a single selected reference volume, the target is built using an iterative and updated pattern, therefore providing a reliable result given a limited number of images. The MC-MoCo method applied in the context of 3D ihMT images significantly decreased the residual motion and outperforms MCFLIRT.