3352
Segmented Twin-resolution Acquisition of Cones Trajectory (STACY) and Coalesced Image Navigator for Free-breathing Cardiac MRI1Magnetic Resonance Systems Research Lab (MRSRL), Stanford University, Stanford, CA, United States, 2Department of Bioengineering, Stanford University, Stanford, CA, United States, 3Magnetic Resonance Systems Research Lab (MRSRL), Department of Electrical Engineering, Stanford University, Stanford, CA, United States, 4Department of Radiology, Stanford University, Stanford, CA, United States
Synopsis
3D image-based navigators (iNAVs) are effective for tracking motion in free-breathing cardiac MRI, though they require a long acquisition window. In this work, we present Segmented Twin-resolution Acquisition of Cones trajectorY (STACY) and the concept of coalesced image navigators. In STACY, different segments of a 3D low-resolution cones trajectory are collected across heartbeats as navigators. Coalesced image navigators are reconstructed by merging data from similarly translated heartbeatsh, leading to better conditioned images than iNAVs from undersampled data collected over individual heartbeats.
Introduction
To deal with motion in free-breathing cardiac MRI, cardiac triggering is commonly used in conjunction with a navigator-based motion-correction technique$$$^1$$$. Image-based navigators (iNAVs) $$$^{2, 3}$$$ are particularly suitable for cardiac applications as they can isolate heart motion from the background.3D iNAVs are attractive for more complete motion monitoring but require aggressively undersampled scanning over a relatively long acquisition window (e.g., about 180ms with a 32-interleave cones design$$$^{3, 4, 5}$$$). As such, motion in the primary data may not be accurately captured by the navigator, and scanning subjects with high heart rates may be challenging.
In this work, we present Segmented Twin-resolution Acquisition of Cones trajectorY (STACY) and the concept of coalesced image navigators. In STACY, different segments of a 3D low-resolution cones trajectory are collected across heartbeats as navigators. Better-conditioned images, named coalesced image navigators, are then reconstructed by merging data from similarly translated heartbeats. Motion is corrected with coalesced image navigators instead of with iNAVs from highly undersampled data.
Segmented Twin-resolution Acquisition of Cones Trajectory (STACY)
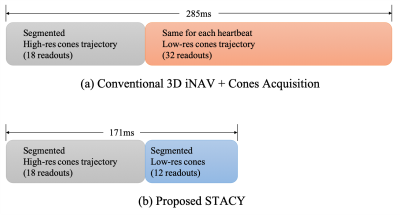
Figures 1(a, b) compare the conventional 3D iNAVs acquisition$$$^3$$$ with the proposed STACY. A key difference is that a different segment of a low-resolution cones trajectory is acquired for each heartbeat in STACY whereas the same cones trajectory is used for all heartbeats in the conventional acquisition.Redesigned cones trajectories$$$^6$$$ are used in STACY, which uses a spiral path on a unit sphere to determine directions of conic interleaves. By subsampling the spiral path, we can divide a cones trajectory into a set of undersampled cones trajectories that cover from north to south poles in k-space to employ individual segment as an iNAV for a particular heartbeat.
Coalesced Image Navigators based Motion Correction
Figure 2(a) illustrates the motion-corrected reconstruction using conventional iNAVs$$$^2$$$. Each segment of the high-resolution cones readouts is corrected by using the iNAV information acquired at the same heartbeat.Here, we propose coalesced image navigators. We define a set of two or more elemental heartbeats as a coalesced heartbeat, and a coalesced image navigator is the low-resolution reconstruction of k-space data of the coalesced heartbeat. The hypothesis is that motion of individual heartbeats can be corrected in the domain of coalesced heartbeats. Also, it may be a reasonable assumption that for every heartbeat, there exists other heartbeats experiencing similar motion given the periodicity of respiratory motion.
Figure 2(b) shows a conceptual description of coalesced iNAV-based motion correction. More specifically, let $$$\{c_j\}$$$ denote an array of coalesced heartbeats and $$$\{r_j\}$$$ be a corresponding array of coalesced iNAVs. Let $$$r_0$$$ be a reference frame and $$$\Delta_j$$$ represent a translation of the j-th coalesced iNAV with respect to $$$r_0$$$. If the i-th heartbeat is a member of p-coalesced heartbeats, $$$(c_{j_1}, \cdots, c_{j_p})$$$, we estimate motion of the i-th heartbeat using coalesced iNAVs as follows:$$\text{translation of i-th hb} \mathrel{+}= \frac{\Delta_{j_1} + \cdots \Delta_{j_p}}{p},$$ which is the average of translations of p-coalesced heartbeats.
We repeat this process with different combinations of coalesced heartbeats. Members of a coalesced heartbeat are chosen based on previous motion estimates to merge similarly translated heartbeats. Initial motion is estimated by using iNAVs of individual heartbeats. For the reference frame, $$$r_0$$$, a low-resolution cones trajectory is acquired over the full acquisition window at a separate heartbeat.
Methods
To test the feasibility of this method, a numerical phantom was generated using MRXCAT$$$^7$$$ for a simulation study. A 1.5T GE Signa scanner and GE 8-channel cardiac coil were used for an in-vivo study. An ATR-SSFP sequence$$$^2$$$ was prescribed with following parameters: TE/TR1/TR2 = 0.62/1.15/4.55ms, $$$70^\circ$$$ flip angle, and 2.8ms readout duration.High- and low-resolution trajectories in STACY were designed with the following prescriptions: FOV = (28, 28, 14)-cm, RES = 1-mm and 6-mm (isotropic). Coalesced heartbeats were constructed by merging three similarly translated heartbeats. The conventional sequence consisted of a phyllotaxis cones trajectory (RES=1.2-mm)$$$^4$$$ and a 32-interleave variable-density cones trajectory (RES=4.4-mm)$$$^3$$$ for iNAVs. The number of readouts for the high-resolution data was 10,980 in both sequences. The number of navigator readouts per heartbeat was 12 and 32, resulting in iNAV acquisition duration of 68.4ms and 182.4ms for STACY and the conventional approach, respectively. L1-ESPIRiT$$$^{8, 9}$$$ was used for reconstruction.
Simulation Study
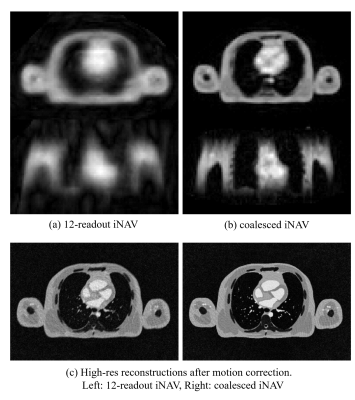
Figures 3(a-b) show image navigators in STACY where the coalesced image navigator showed less aliasing artifact compared to a 12-interleave iNAV. Figure 3(c) compares motion-corrected images derived from 12-interleave iNAVs and from the proposed method. Due to severe aliasing artifacts, 12-interleave iNAVs were ill-conditioned for motion correction while the proposed method produced a superior reconstruction result.Preliminary In-vivo Study
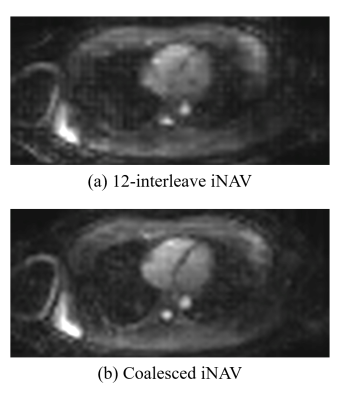
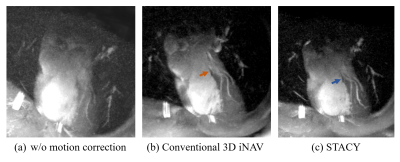
A volunteer with a heart rate of 80 beat per minute (bpm) was scanned with conventional and proposed sequences. An iNAV at a particular heartbeat is illustrated in Fig. 4(a) whereas a corresponding coalesced iNAV is shown in Fig. 4(b). The coalesced iNAV demonstrates improved quality due to the better conditioning. Figures 5(a-c) are reconstructions of the left anterior descending coronary artery (LAD). Although the LAD is observable to some extent without any motion correction, the conventional and proposed motion-corrected reconstructions lead to improved vessel depiction, with STACY producing slightly better sharpness in this case.Conclusion
A new acquisition and motion-correction scheme was proposed that corrects motion with coalesced navigators from similarly translated heartbeats rather than highly undersampled iNAVs from individual heartbeats.Acknowledgements
The authors gratefully acknowledge the support from NIH grant HL127039 and GE Healthcare.References
1. M. A. Bernstein, K. F. King, and X. J. Zhou, Handbook of MRI pulse sequences. Elsevier, 2004.
2. H. H. Wu, P. T. Gurney, B. S. Hu, D. G. Nishimura, and M. V. McConnell, "Free-breathing multiphase whole-heart coronary MR angiography using image-based navigators and three-dimensional cones imaging," Magnetic resonance in medicine, vol. 69, no. 4, pp. 1083–1093, 2013.
3. N. O. Addy, R. R. Ingle, J. Luo, C. A. Baron, P. C. Yang, B. S. Hu, and D. G. Nishimura,"3D image-based navigators for coronary MR angiography," Magnetic resonance in medicine, vol. 77, no. 5, pp. 1874–1883, 2017.
4. M. O. Malave, C. A. Baron, N. O. Addy, J. Y. Cheng, P. C. Yang, B. S. Hu, and D. G. Nishimura, "Whole-heart coronary MR angiography using a 3D cones phyllotaxis trajectory," Magnetic resonance in medicine, vol. 81, no. 2, pp. 1092–1103, 2019.
5. J. Luo, N. O. Addy, R. R. Ingle, C. A. Baron, J. Y. Cheng, B. S. Hu, and D. G. Nishimura, "Nonrigid motion correction with 3D image-based navigators for coronary MR angiography," Magnetic resonance in medicine, vol. 77, no. 5, pp. 1884–1893, 2017.
6. K. E. Jang, S. P. Koundinyan, D. G. Nishimura, and S. S. Vasanawala, "Redesigned Variable Density Cones Trajectory for High Resolution MR Imaging," in Proceedings of the 27th Annual Meeting of the ISMRM, 2018.
7. L. Wissmann, C. Santelli, W. P. Segars, and S. Kozerke, "MRXCAT: Realistic numerical phantoms for cardiovascular magnetic resonance," Journal of Cardiovascular Magnetic Resonance, vol. 16, no. 1, p. 63, 2014.
8. A. Beck and M. Teboulle, "A fast iterative shrinkage-thresholding algorithm for linear inverse problems," SIAM journal on imaging sciences, vol. 2, no. 1, pp. 183–202, 2009.
9. M. Uecker, P. Lai, M. J. Murphy, P. Virtue, M. Elad, J. M. Pauly, S. S. Vasanawala, and M. Lustig, "ESPIRiT – an eigenvalue approach to autocalibrating parallel MRI: where SENSE meets GRAPPA," Magnetic resonance in medicine, vol. 71, no. 3, pp. 990–1001, 2014.
Figures