3340
Non-rigid “image” registration in k-space
Thomas Küstner1,2,3, Christopher Gilliam4, Thierry Blu5, Martin Schwartz3,6, Gastao Cruz1, Jiazhen Pan3, Christian Würslin2, Nina F Schwenzer7, Holger Schmidt7, Bin Yang3, Konstantin Nikolaou8, René M Botnar1, Claudia Prieto1, and Sergios Gatidis2,8
1Biomedical Engineering Department, School of Biomedical Engineering and Imaging Sciences, King's College London, London, United Kingdom, 2Medical Image and Data Analysis (MIDAS), University Hospital Tübingen, Tübingen, Germany, 3Institute of Signal Processing and System Theory, University of Stuttgart, Stuttgart, Germany, 4RMIT University, Melbourne, Australia, 5Chinese University Hong Kong, Hong Kong, Hong Kong, 6Section on Experimental Radiology, University Hospital Tübingen, Tübingen, Germany, 7University of Tübingen, Tübingen, Germany, 8Department of Radiology, University Hospital Tübingen, Tübingen, Germany
1Biomedical Engineering Department, School of Biomedical Engineering and Imaging Sciences, King's College London, London, United Kingdom, 2Medical Image and Data Analysis (MIDAS), University Hospital Tübingen, Tübingen, Germany, 3Institute of Signal Processing and System Theory, University of Stuttgart, Stuttgart, Germany, 4RMIT University, Melbourne, Australia, 5Chinese University Hong Kong, Hong Kong, Hong Kong, 6Section on Experimental Radiology, University Hospital Tübingen, Tübingen, Germany, 7University of Tübingen, Tübingen, Germany, 8Department of Radiology, University Hospital Tübingen, Tübingen, Germany
Synopsis
Non-rigid motion estimation is an important task in correction of respiratory and cardiac motion. Usually this problem is formulated in image space via diffusion, parametric-spline or optical flow methods. For these applications non-rigid motion commonly needs to be estimated from cardiac or respiratory states which are highly subsampled in k-space. Image-based registration can be impaired by aliasing artefacts or by estimation from low-resolution images. In this work, we propose a novel non-rigid registration technique directly in k-space based on optical flow. The proposed method is compared against image-based registrations and tested on fully-sampled and highly-accelerated 3D motion-resolved MR imaging.
Introduction
Fast and accurate motion estimation is an important task for prospective or retrospective motion correction techniques which can be applied to for example image guided interventions1, cardiac assessment2 or MR-based motion correction of PET data3,4. Data acquisitions for these applications are usually accelerated by Compressed Sensing. A particular interest and challenge lies in the derivation of reliable 3D motion fields from the subsampled data which capture non-rigid deformations, such as respiratory or cardiac movement.Motion-compensated image reconstructions5-11 integrate the motion field estimation, and respective motion correction, into the reconstruction process. These methods require reliable motion-resolved images from which the motion fields can be estimated. Motion field estimation can be controlled or supported by external motion surrogate signals5,6, initial motion field estimates7,8, from motion-aliased images10 or low-frequency image contents11.
The non-rigid motion estimation problem is usually formulated in image space as a diffusion-based12, parametric spline-based13 or optical flow-based method14. However, in case of highly subsampled data, aliasing artefacts in the image can impair the registration and/or low-resolution images do not provide sufficient motion information. Carrying out an aliasing-free registration in k-space for accelerated acquisitions would be desirable.
In this work, we propose a novel approach by formulating the non-rigid registration directly in k-space based on optical flow equations. We will first describe the basic concepts on the image-based 3D non-rigid registration, denoted as Local All-Pass (LAP) which we have presented previously4,15,16. We illustrate then its extension to a k-space based 3D non-rigid registration. The proposed method is compared against image-based registrations and tested on fully-sampled and highly subsampled 3D motion-resolved MR imaging (respiratory and cardiac motion).
Methods
The key idea of LAP is that any non-rigid deformation can be regarded as local rigid displacements. These displacements can be modeled as local all-pass filter operations. Under the assumption of local brightness consistency, the optical flow equation of a rigid displacement can be equivalently stated in Fourier space$$I_r(\underline{x})=I_m(\underline{x}-\underline{u})\Leftrightarrow\hat{I}_r(\underline{k})\cong\hat{I}_m(\underline{k})\mathrm{e}^{-j\underline{u}^T \underline{k}}\qquad(1)$$for deforming a moving image $$$I_m$$$ to a reference image $$$I_r$$$ via a deformation field $$$\underline{u}(\underline{x})$$$ at position $$$\underline{x}=[x,y,z]^T$$$, with $$$\hat{I}_r(\underline{k})$$$ and $$$\hat{I}_m(\underline{k})$$$ being the k-spaces of the moving and reference image at $$$\underline{k}=[k_x,k_y,k_z]^T$$$. The linear phase ramp can be regarded as an all-pass filter $$$\hat{h}(\underline{k},\underline{x})=\mathrm{e}^{-j\underline{u}^T\underline{k}}=\hat{p}(\underline{k})/\hat{p}(-\underline{k})$$$ that can be split into a forward $$$\hat{p}(\underline{k})$$$ and backward filter $$$\hat{p}(-\underline{k})$$$ with $$$p(\underline{x})\in\mathbb{R}$$$ which is all-pass by design17. Global non-rigid deformation is then modelled as local rigid displacements and hence the problem of non-rigid image registration becomes estimating the appropriate local all-pass filter for different $$$\underline{x}$$$ in a cubic window $$$\mathcal{W}$$$. Selecting an optimal filter basis $$$p_n$$$ fulfilling diffeomorphic and smooth flow (e.g. Gaussian), allows to conclude the formulation in image domain$$\min\limits_{{c_n}}\sum\limits_{\underline{x}\in\mathcal{W}}\mathcal{D}\left(p(\underline{x})\ast\,I_m(\underline{x}),p(-\underline{x})\ast\,I_r(\underline{x})\right)\text{ s.t. }p(\underline{x})=p_0(\underline{x})+\sum\limits_{n=1}^{N}c_np_n(\underline{x})\quad\forall\underline{x}\in\mathbb{R}^3\qquad(2)$$for which at each image position $$$\underline{x}$$$ the $$$N$$$ optimal filter coefficients $$$c_n$$$ are estimated18 by minimizing the dissimilarity $$$\mathcal{D}$$$ (e.g. mean-squared-error, MSE) between $$$I_m$$$ and $$$I_r$$$.
In order to carry out the operations in Fourier domain, we need to consider the local windowing $$$\mathcal{W}$$$$$I_W(\underline{x})=\mathcal{W}(\underline{x})\cdot\,I(\underline{x})\Leftrightarrow\hat{I}_W(\underline{k})=T(\underline{k})\ast\,\hat{I}(\underline{k})\qquad(3)$$which corresponds in k-space to the convolution by a phase-modulated (for various $$$\underline{x}$$$ positions) tapering function $$$T(\underline{k})$$$. Transforming Eq.2 in Fourier domain$$\min\limits_{{c_n}}\sum\limits_{\underline{k}\in\mathbb{R}^3}\mathcal{D}\left(T(\underline{k})\ast\left(\hat{p}(\underline{k})\hat{I}_{m}(\underline{k})\right),\,T(\underline{k})\ast\left(\hat{p}(-\underline{k})\hat{I}_{r}(\underline{k})\right)\right)\\\text{ s.t. }\hat{p}(\underline{k})=\hat{p}_0(\underline{k})+\sum\limits_{n=1}^{N}c_n\hat{p}_n(\underline{k})\quad\forall\underline{k}\in\mathbb{R}^3\qquad(4)$$yields the k-space version of optical-flow based “image” registration. In order to deal with motion of various strength, a multi-resolution approach over $$$M$$$ iterations is applied as depicted in Fig.1 in which the size of $$$\mathcal{W}$$$, respectively the half filter support $$$\hat{p}$$$, is decreased, i.e. coarse-to-fine estimation. Please note that summation is required over all $$$\underline{k}$$$ positions and for shifted tapering supports. Hence, for carrying out a registration over the complete spectral support requires $$$2\cdot(k_x\cdot\,k_y\cdot\,k_z)^2$$$ convolutions at each iteration which can be very demanding, e.g. $$$k_x=k_y=256,k_z=144$$$ requires $$$178\cdot 10^{12}$$$ convolutions. Hence, in order to make it computationally feasible an approximation of the registration procedure is applied by using a truncated tapering support of size $$$|\mathcal{W}|=|T|$$$ and a subsampled evaluation on regular grid and at sampled k-space locations. The deformation field $$$\underline{u}$$$ in image domain can be directly derived from the all-pass filter$$\underline{u}=j\left.\frac{\partial\ln\hat{h}(\underline{k})}{\partial\underline{k}}\right|_{\underline{k}=\underline{0}}\Leftrightarrow\underline{u}=2\left\lbrack\frac{\sum_{\underline{x}}xp(\underline{x})}{\sum_{\underline{x}}p(\underline{x})},\frac{\sum_{\underline{x}}yp(\underline{x})}{\sum_{\underline{x}} p(\underline{x})},\frac{\sum_{\underline{x}}zp(\underline{x})}{\sum_{\underline{x}} p(\underline{x})}\right\rbrack^T.\qquad(5)$$The proposed registration is evaluated in image and k-space for fully-sampled and retrospectively subsampled datasets for 4D motion-resolved imaging as stated in Table 1. Furthermore, a simulated non-rigid deformation field $$$\underline{u}_\text{sim}$$$ was applied to the datasets to derive angular error $$$\text{AE}=\arg(\underline{u},\underline{u}_\text{sim})$$$ and end-point error $$$\text{EE}=\Vert\underline{u}-\underline{u}_\text{sim}\Vert_2$$$ as average and standard deviation over all voxel positions.
Results
Evaluation of the smooth deformation in all subjects is shown in Fig.2. Fig.3 shows the exemplary results of a respiratory-resolved and Fig.4 of a cardiac-resolved dataset. Non-rigid registration in k-space is possible, but accuracy is determined by amount of operations in k-space, i.e. more operations can result in better approximation at the expense of longer run-time. K-space registration shows high agreement with reference fully-sampled image-based registration. For highly accelerated acquisitions, image-based registration fails whereas k-space registration still provides similar performance.Conclusion
Non-rigid registration in k-space is feasible and provides reliable deformation fields especially for highly accelerated imaging for which image-based registration is impaired. In the future, we want to investigate if registration can be speed-up by GPU and/or if the filter kernels can be estimated from training via neural networks instead of being explicitly stated.Acknowledgements
The authors would like to thank Carsten Gröper and Gerd Zeger for data acquisition and Brigitte Gückel for study coordination.References
1. McClelland JR, Blackall JM, Tarte S, Chandler AC, Hughes S, Ahmad S, Landau DB, Hawkes DJ. A continuous 4D motion model from multiple respiratory cycles for use in lung radiotherapy. Medical Physics 2006;33(9):3348-3358.2. Manke D, Nehrke K, Börnert P, Rösch P, Dössel O. Respiratory motion in coronary magnetic resonance angiography: a comparison of different motion models. Journal of Magnetic Resonance Imaging 2002;15(6):661-671.
3. Munoz C, Neji R, Cruz G, Mallia A, Jeljeli S, Reader AJ, Botnar RM, Prieto C. Motion‐corrected simultaneous cardiac positron emission tomography and coronary MR angiography with high acquisition efficiency. Magnetic Resonance in Medicine 2018;79(1):339-350.
4. Küstner T, Schwartz M, Martirosian P, Gatidis S, Seith F, Gilliam C, Blu T, Fayad H, Visvikis D, Schick F. MR-based respiratory and cardiac motion correction for PET imaging. Medical image analysis 2017;42:129-144.
5. Odille F, Vuissoz PA, Marie PY, Felblinger J. Generalized reconstruction by inversion of coupled systems (GRICS) applied to free‐breathing MRI. Magnetic Resonance in Medicine 2008;60(1):146-157.
6. Cordero-Grande L, Teixeira RPA, Hughes EJ, Hutter J, Price AN, Hajnal JV. Sensitivity encoding for aligned multishot magnetic resonance reconstruction. IEEE Transactions on Computational Imaging 2016;2(3):266-280.
7. Batchelor P, Atkinson D, Irarrazaval P, Hill D, Hajnal J, Larkman D. Matrix description of general motion correction applied to multishot images. Magnetic Resonance in Medicine 2005;54(5):1273-1280.
8. Atkinson D, Hill DL, Stoyle PN, Summers PE, Keevil SF. Automatic correction of motion artifacts in magnetic resonance images using an entropy focus criterion. IEEE transactions on medical imaging 1997;16(6):903-910.
9. Ong F, Lustig M. Joint Non-Rigid Motion Estimation and Image Reconstruction via Sparse Blind Deconvolution. Proceedings of the International Society for Magnetic Resonance in Medicine (ISMRM); 2017. p 3937.
10. Haskell MW, Cauley SF, Bilgic B, Hossbach J, Splitthoff DN, Pfeuffer J, Setsompop K, Wald LL. Network Accelerated Motion Estimation and Reduction (NAMER): Convolutional neural network guided retrospective motion correction using a separable motion model. Magnetic Resonance in Medicine 2019;82(4):1452-1461.
11. Usman M, Latif S, Asim M, Qadir J. Motion Corrected Multishot MRI Reconstruction Using Generative Networks with Sensitivity Encoding. arXiv preprint arXiv:190207430 2019.
12. Thirion J-P. Image matching as a diffusion process: an analogy with Maxwell's demons. Medical image analysis 1998;2(3):243-260.
13. Rueckert D, Sonoda LI, Hayes C, Hill DL, Leach MO, Hawkes DJ. Nonrigid registration using free-form deformations: application to breast MR images. IEEE transactions on medical imaging 1999;18(8):712-721.
14. Horn BK, Schunck BG. Determining optical flow. Artificial intelligence 1981;17(1-3):185-203.
15. Gilliam C, Küstner T, Blu T. 3D motion flow estimation using local all-pass filters. IEEE International Symposium on Biomedical Imaging (ISBI); 2016. p 282-285.
16. Küstner T, Schwartz M, Gatidis S, Schwenzer NF, Schmidt H, Yang B, Gilliam C, Blu T, Schick F. Local All-Pass Filter (LAP): Efficient Optical Flow-Based Image Registration. Proceedings of the ISMRM Workshop on Motion Correction in MRI and MRS; 2017.
17. Gilliam C, Blu T. Local all-pass filters for optical flow estimation. IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP); 2015. p 1533-1537.
18. Blu T, Moulin P, Gilliam C. Approximationorder of the lap optical flow algorithm. IEEE International Conference on Image Processing (ICIP); 2015. p 48-52.
19. Küstner T, Bustin A, Neji R, Botnar R, Prieto C. 3D Cartesian Whole-heart CINE MRI Exploiting Patch-based Spatial and Temporal Redundancies. Proceedings of the European Society for Magnetic Resonance in Medicine (ESMRMB); 2019.
Figures
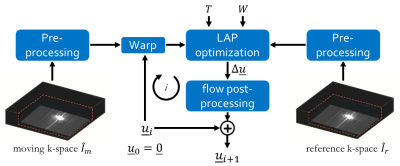
Fig. 1:
Multi-resolution non-rigid registration in k-space with the proposed k-space
version of the local all-pass (LAP). In each multi-resolution loop i, the motion field u is improved on a coarse-to-fine scheme by adapting filter support
W and tapering support T. If required pre-processing steps,
such as filtering or scaling can be applied. In this work, no pre-processing is
used.
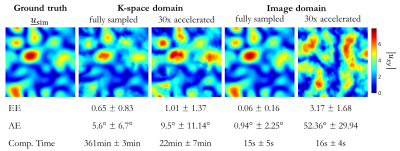
Fig.
2: Results of registration in image and k-space for a simulated smooth
deformation field usim (ground
truth) which was applied to all 36 respiratory and 10 cardiac subjects of the
fully-sampled and accelerated acquisition (30x). Registration was conducted
between deformed image Im(x)
= Ir(x+usim) and
reference image Ir. Mean
and standard deviation over all subjects and all voxels are stated as well as
computational time. Exemplary absolute displacement in-plane from estimated
deformation field in central slice is depicted (top row).
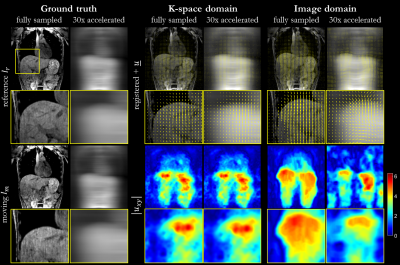
Fig.
3: Non-rigid registration in image and k-space for respiratory motion. Registration
was conducted between end-expiratory and end-inspiratory phase. Reference (end-expiratory), moving
(end-inspiratory) and registered images with overlaid forward deformation field
(end-expiratory to end-inspiratory) are depicted for fully-sampled and
accelerated (30x) acquisition as well as absolute displacement in-plane from
estimated deformation field in central slice. Zoomed images of liver dome show
consistent results for k-space domain to fully-sampled in image domain.

Fig. 4:
Non-rigid registration in image and k-space for cardiac motion. Registration
was conducted between systolic and diastolic phase. Reference (diastolic), moving (systolic) and
registered images with overlaid forward deformation field are depicted for
fully-sampled and accelerated (30x) acquisition as well as absolute
displacement in-plane from estimated deformation field in central slice. Zoomed
images reveal consistent results for k-space domain to fully-sampled in image
domain, whereas 30x accelerated registration in image domain fails.
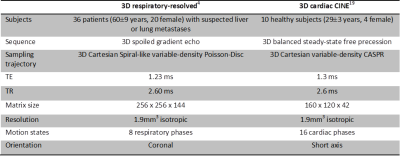
Table 1: 4D (3D+time) motion-resolved MR imaging
datasets and acquisition parameters.