3338

Quantitative abdominal imaging using 3D motion-robust MR fingerprinting
Max van Riel1,2, Zidan Yu2,3, Shota Hodono2,3, Ding Xia2, Hersh Chandarana2, and Martijn A. Cloos2,3
1Department of Biomedical Engineering, Eindhoven University of Technology, Eindhoven, Netherlands, 2Center for Advanced Imaging Innovation and Research and Bernard and Irene Schwartz Center for Biomedical Imaging, Department of Radiology, New York University School of Medicine, New York, NY, United States, 3Sackler Institute of Graduate Biomedical Sciences, New York University School of Medicine, New York, NY, United States

Synopsis

We demonstrate a 3D MR fingerprinting sequence for quantitative abdominal imaging. The sequence was made robust to motion by modifying the order of acquisition to allow for free-breathing imaging. Furthermore, the flip angle pattern was optimized using the Cramér-Rao Lower Bound to increase the efficiency of the sequence. A phantom was used to validate the new sequence and it was shown that the motion-robust ordering reduced motion-related artefacts. In vivo results showed reduced artefacts as well. We conclude that it is possible to generate B1-robust quantitative T1 and proton density maps at a clinically usable resolution within 5 minutes.

Introduction

Magnetic Resonance Fingerprinting (MRF) is a technique that allows for fast, simultaneous quantification of multiple parameters, such as T1, T2, proton density (PD), and/or B1 field strength.1,2 Extending MRF to 3D allows for a larger coverage and a better through-plane resolution.3,4 However, when imaging the abdomen, motion can reduce the quality of the parameter maps.5 Moreover, B0 and B1 inhomogeneities are particularly problematic, due to air pockets and destructive interference of the B1 field.6 In this work, we present a motion-robust 3D MRF sequence for quantitative abdominal imaging. The method was validated using a moving phantom and applied in vivo during free-breathing measurements.

Methods

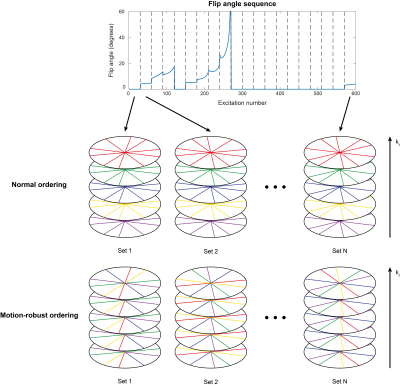
Sequence design
To generate the fingerprints, a Fast Low-Angle SHot (FLASH) sequence with variable flip angles was used. All excitations were RF- and gradient-spoiled. A non-selective adiabatic inversion pulse was applied before the start of the sequence to enhance the T1-encoding capability of the fingerprints.

The k-space data was acquired in a 3D stack-of-stars trajectory.7 Originally, with every subsequent excitation, the spoke with the same phase encoding index but a different azimuthal angle was acquired (normal ordering). In the proposed free-breathing sequence, the kz-index of the acquired line is increased by one with every excitation while keeping the azimuthal angle constant (motion-robust ordering, see Figure 1). This way, adjacent spokes in the phase encoding direction are acquired in quick succession, reducing motion-related artefacts. This creates several sets, where each set consists of as many consecutive spokes as the number of slices.

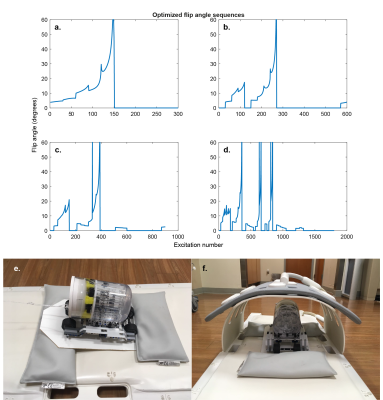
To minimize the variance of the estimated parameters, the flip angle pattern was optimized using the relative Cramér-Rao Bound (CRB)8–12 for T1 and B1. The peak flip angle was limited to 60 degrees to ensure that the necessary transmit voltage could be implemented on the scanner. Sequences with 300, 600, 900, and 1800 flip angles were optimized (Figure 2 a-d) in MATLAB (The MathWorks Inc., Natick, MA, USA), using the CasADI13 toolbox for automatic differentiation and the Interior Point OPTimizer (Ipopt)14 as optimization algorithm.

Image acquisition
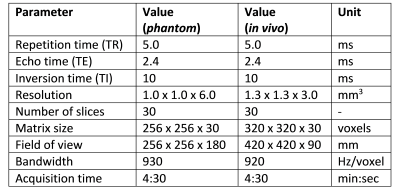
All experiments were performed on a clinical 3T MRI scanner (Prisma, Siemens, Erlangen, Germany). A phantom containing glass tubes with different T1 values was placed on a cart made from LEGO® (The Lego Group, Billund, Denmark), riding on a slope of ~7 degrees and controlled by a motor outside the scanner room (RWTH Mindstorms NXT Toolbox for MATLAB, RWTH Aachen University, Germany). An 18-channel body coil was placed over the phantom assembly during the scan (Figure 2). The same coil was used for the in vivo scan. The parameters used for all imaging experiments are summarized in Table 1. The acquisition time was kept constant by acquiring more shots for shorter sequences. A previously published 2D MRF implementation15 was used as a reference scan to validate the quantitative T1 values without motion.

Dictionary construction
Our dictionary contained 17600 fingerprints, each with a unique combination of T1 and B1 values. The T1 values used for the dictionary ranged from 50 ms to 3764 ms with increments of 2.5%, while the relative B1 field strengths ranged from 0.02 to 2.0 in steps of 0.02. The Bloch equations were used to simulate the effect of the RF-pulses on a single isochromat for each parameter combination. The resulting signals within each set were averaged and each fingerprint was normalized to have unit Euclidean norm.

Dictionary matching
Each set was reconstructed separately using the Nonuniform Fast Fourier Transform (NUFFT)16, resulting in a sequence of images. The best matching dictionary entries for every voxel were then used to obtain the parametric maps.1

Results & Discussion

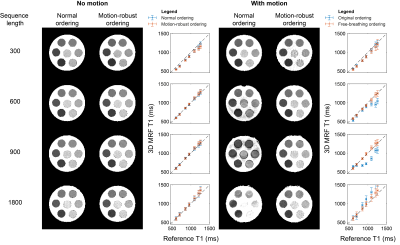
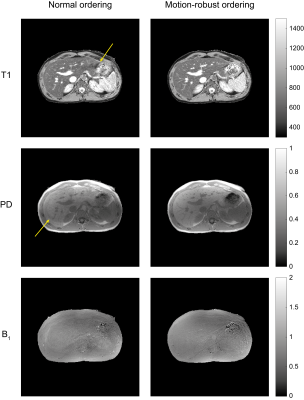
The results from the phantom scan can be seen in Figure 4. The sequence with 300 flip angles was not as accurate for higher T1 values. Most likely, the time from one inversion to the next is too short to observe the slow dynamics of the long T1 samples. The longest sequence (with the fewest number of shots) showed too much variability in the T1 estimates due to the increased undersampling artefacts. The sequences with 600 and 900 flip angles demonstrated fewer artefacts and better agreement with the reference when using the motion-robust ordering.

The motion artefacts were not visible for all periods of the motion pattern when not using the motion-robust ordering. This was probably caused by interference with the timing of the sequence due to the regular motion of the phantom. Since in vivo breathing motion is not as regular and may occur at any frequency, the proposed ordering is important to prevent motion artefacts.

The sequence with 600 flip angles was selected to be tested in vivo. The motion-robust ordering showed better detail in the T1 map and reduced the motion-related artefacts (Figure 5). In particular, a clear artifact is visible in both the T1 and B1 maps acquired using the normal ordering.

Conclusion

A free-breathing MR Fingerprinting sequence was demonstrated for B1-robust quantitative abdominal imaging. The sequence was validated in a phantom and demonstrated in vivo. With this motion-robust MRF implementation it is possible to collect crisp PD images and accurate T1 maps of the abdomen at a clinically usable resolution within 5 minutes.

Acknowledgements

The research reported in this publication was supported by the NIH/NIBIB grant R01 EB026456, NIH/NIAMS grant R01 AR070297, and performed under the rubric of the Center for Advanced Imaging Innovation and Research, an NIBIB Biomedical Technology Resource Center (P41 EB017183). Furthermore, I would like to express my gratitude towards the Holland Scholarship from the Dutch Ministry of Education, Culture and Science and the Amandus H. Lundqvist Scholarship Program for supporting this internship project.

References

1. Ma D, Gulani V, Seiberlich N, et al. Magnetic resonance fingerprinting. Nature. 2013;495(7440):187-192. doi:10.1038/nature11971

2. Cloos MA, Knoll F, Zhao T, et al. Multiparametric imaging with heterogeneous radiofrequency fields. Nat Commun. 2016;7:1-10. doi:10.1038/ncomms12445

3. Ma D, Jiang Y, Chen Y, et al. Fast 3D Magnetic Resonance Fingerprinting for a Whole-Brain Coverage. Magn Reson Med. 2018;79(4):2190-2197. doi:10.1002/mrm.26886

4. Fujimoto K, Cloos MA, Urushibata Y, Okada T. Cortical T1 mapping with 3D MR Fingerprinting at 7T using a single transmit channel. In: Proceedings of the 26th Annual Meeting of ISMRM, Paris, France; 2018:1135.

5. Yu Z, Zhao T, Assländer J, Lattanzi R, Sodickson DK, Cloos MA. Exploring the sensitivity of magnetic resonance fingerprinting to motion. Magn Reson Imaging. 2018;54:241-248. doi:10.1016/j.mri.2018.09.002

6. Merkle EM, Dale BM. Abdominal MRI at 3.0 T: The basic revisited. Am J Roentgenol. 2006;186(6):1524-1532. doi:10.2214/AJR.05.0932

7. Block KT, Chandarana H, Milla S, et al. Towards Routine Clinical Use of Radial Stack-of-Stars 3D Gradient-Echo Sequences for Reducing Motion Sensitivity. J Korean Soc Magn Reson Med. 2014;18(2):87-106. doi:10.13104/jksmrm.2014.18.2.

8. Kay SM. Fundamentals of Statistical Signal Processing: Estimation Theory. Vol 1. Upper Saddle River, NJ: Prentice Hall PTR; 1993.

9. Teixeira RPAG, Malik SJ, Hajnal J V. Joint System Relaxometry (JSR) and Cramér-Rao Lower Bound Optimization of Sequence Parameters: A Framework for Enhanced Precision of DESPOT T1 and T2 Estimation. Magn Reson Med. 2018;79(1):234-245. doi:10.1002/mrm.26670

10. Zhao B, Haldar JP, Liao C, et al. Optimal Experiment Design for Magnetic Resonance Fingerprinting: Cramér-Rao Bound Meets Spin Dynamics. IEEE Trans Med Imaging. 2019;38(3):844-861. doi:10.1109/TMI.2018.2873704

11. Lee PK, Watkins LE, Anderson TI, Buonincontri G, Hargreaves BA. Flexible and efficient optimization of quantitative sequences using automatic differentiation of Bloch simulations. Magn Reson Med. 2019;82(4):1438-1451. doi:10.1002/mrm.27832

12. Assländer J, Lattanzi R, Sodickson DK, Cloos MA. Optimized quantification of spin relaxation times in the hybrid state. Magn Reson Med. 2019;82(4):1385-1397. doi:10.1002/mrm.27819

13. Andersson JAE, Gillis J, Horn G, Rawlings JB, Diehl M. CasADi – A software framework for nonlinear optimization and optimal control. Math Program Comput. 2019;11(1):1-36. doi:10.1007/s12532-018-0139-4

14. Andreas W, Biegler LT. On the implementation of an interior-point filter line-search algorithm for large-scale nonlinear programming. Math Program. 2006;106(1):25-57. doi:10.1007/s10107-004-0559-y

15. Cloos MA, Assländer J, Abbas B, et al. Rapid Radial T 1 and T 2 Mapping of the Hip Articular Cartilage With Magnetic Resonance Fingerprinting. J Magn Reson Imaging. 2019;50(3):810-815. doi:10.1002/jmri.26615

16. Fessler JA, Sutton BP. Nonuniform Fast Fourier Transforms Using Min-Max Interpolation. IEEE Trans Signal Process. 2003;51(2):560-574. doi:10.1109/TSP.2002.807005

Figures

Figure 1: Trajectory of the proposed free-breathing MRF sequence. Each excitation corresponds to a single readout line. These lines are grouped into sets, with each set containing as many spokes as the number of slices. In the normal ordering, all lines with the same phase encoding are acquired each time the sequence is played out. All red lines are acquired first, followed by the green, blue, yellow, and purple lines respectively. In the motion-robust ordering, all lines within one set with the same angle but a different phase encoding index were acquired successively.

Figure 2: (a-d): Optimized flip angle patterns for 300 (a), 600 (b), 900 (c), and 1800 (d) flip angles. (e-f): Experimental setup with the movable phantom positioned on a slope (e), with the body coil placed over it (f).

Table 1: Image acquisition parameters used in both the phantom and the in vivo experiments.

Figure 4: T1 maps and correlation plots between the 3D MRF sequence and the reference scan without (left) and with (right) motion, with both orderings, and for all four sequence lengths for which the flip angles were optimized. In the correlation plots, the horizontal axis shows the estimated T1 of each tube using the reference 2D MRF sequence, with the 3D MRF sequence (using either ordering) on the vertical axis. The errorbars indicate the standard deviation of the estimated T1 of each tube for both methods in their respective directions, and the dashed line indicates the identity line.

Figure 5: Quantitative in vivo T1 (top row), PD (middle row), and B1 (bottom row) maps for the normal ordering (left column) and the motion-robust ordering (right column) using the sequence with 600 flip angles. The motion-robust ordering reveals more details in the T1 map, and removes the motion-related artefacts visible in both the T1 and PD maps (indicated with yellow arrows).

Proc. Intl. Soc. Mag. Reson. Med. 28 (2020)
3338