3328

Helmholtz Inversion using Unconstrained Optimization for MR Elastography of the Lung: A Comparison to Direct Inversion

Huiming Dong^1,2, Rizwan Ahmad², and Arunark Kolipaka^1,2
¹Department of Radiology, The Ohio State University Wexner Medical Center, Columbus, OH, United States, ²Department of Biomedical Engineering, The Ohio State University, Columbus, OH, United States

Synopsis

Lung stiffness is a potential biomarker for multiple lung diseases. MR elastography (MRE) allows non-invasive measurement of lung stiffness. However, it is challenging to estimate stiffness using direct Helmholtz inversion due to low signal-to-noise ratio (SNR) from lung MRE. In this work, a compressed-sensing-based Helmholtz inversion is proposed where noise is reduced via Laplacian of Gaussian (LoG) and Morozov’s discrepancy principle, while the sparsity of stiffness map is explored in a wavelet domain. Results demonstrated that the proposed inversion yielded robust stiffness estimation and successfully detected higher stiffness at total lung capacity (TLC) compared to residual volume (RV).

Introduction

Direct inversion (DI) of the Helmholtz equation is an established inversion to estimate tissue stiffness using MR elastography (MRE) data [1, 2]. Under the presence of noise and low wave penetration, correctly estimating stiffness can be challenging because the Laplacian operation within the Helmholtz equation can amplify the noise while obtaining spatial derivatives from the measured displacement, leading to biased stiffness estimates.
This becomes more problematic in the case of estimating shear stiffness of the lung in which the low tissue density and short T2* result in considerably low signal-to-noise ratio (SNR) during lung MRE. It is appreciated that the normal function of the lung is closely associated with its gross topographically heterogeneous mechanical properties which can only be invasively quantified using current diagnostic tools [3], making non-invasive in vivo lung MRE a valuable yet challenging technique [4-6].
To reduce the effect of noise, a large-size kernel (e.g., 13x13 or larger) is usually used to estimate the Laplacian of the displacement field. This strategy offers improved derivative estimation by using the information from a wide coverage of pixels, making the Laplacian operation less sensitive to local fluctuations resulted by noise. Despite its practical significance, a large kernel will potentially reduce the achievable spatial resolution of the stiffness map. Additionally, large kernel sizes cannot resolve the problem of robustly/stably estimating stiffness because the low SNR in the lung MRE data is the main concern.
In this work, a compressed-sensing-based Helmholtz inversion using unconstrained optimization has been proposed where noise is reduced from the measured data using Laplacian of Gaussian (LoG) and Morozov’s discrepancy principle [7], while the sparsity of stiffness map in wavelet domain is explored.

Method

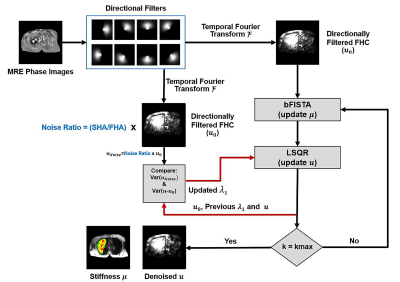
Theory
The optimization problem is described by the following cost function:
$$$J(μ,u)=\underset{μ, u}{argmin}\space||c·LoG(u)·μ-u||\small{{2 \atop 2 }}+λ_1\||u-u_0\||\small{{2 \atop 2 }}+λ_2\||ψ(μ)||_1$$$
where c = -1/(ρω²), ω is the applied mechanical frequency, LoG is the Laplacian of Gaussian operator, µ is the stiffness map of interest, u is the pursued tissue displacement, u₀ is the measured tissue displacement prior to denoising, ψ is a non-decimated wavelet transform and λ₁, λ₂ are regularization coefficients. The first term guarantees data fidelity (i.e., the Helmholtz equation). The second term allows the pursued displacement u to deviate from the measured displacement u₀, reducing undesirable noise. The third term ensures the sparsity of stiffness map in the wavelet domain. In this work, the Gaussian operator was chosen to have a full width at half maximum (FWHM) of 13 pixels for LoG.
Figure 1 demonstrates the details of the proposed optimization technique. The regularization coefficient λ₁ is automatically controlled via Morozov’s discrepancy principle during each iteration to allow different amount of denoising by comparing the measured noise (which is defined as noise ratio x u₀) and the difference between u and u₀, whereas λ₂ is specially tuned for lung MRE. Balanced fast iterative/shrinkage thresholding algorithm (bFISTA) and the least-square method (LSQR) were used in optimizing the cost function [8,9].
Lung MRE
Lung MRE was performed on 5 healthy subjects using a modified breath-hold SE-EPI MRE sequence reported in a previous feasibility study [10]. Imaging parameters included: TE/TR=11.6/400 ms; FOV=400x400x10 mm³; reconstruction matrix=256x256; mechanical frequency=50 Hz; MEG frequency=250 Hz; three-directional motion encoding; 4 MRE phase offsets. Lung density of each volunteer was also measured at RV and TLC as described in [10].
Image Analysis
Lung shear stiffness at RV and total lung capacity TLC was estimated using the proposed inversion algorithm and the standard DI with 17x17 Romano filter in MRElab (Mayo Clinic, Rochester, MN). For both methods, a 4th-order Butterworth bandpass directional filter was applied in eight directions with cutoff values of 4–40 waves/FOV for RV and 2–40 waves/FOV for TLC to remove the longitudinal and reflected waves as described previously [10].

Results and Discusssion

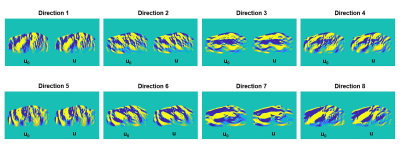
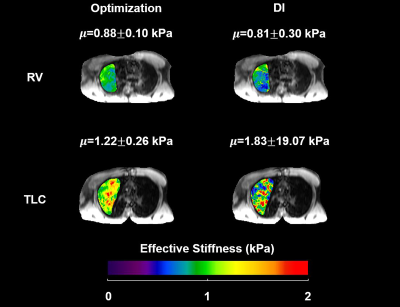
Figure 2 compared the measured displacement and the displacement generated from the proposed inversion technique for each direction. The reconstructed displacement contains less noise compared to the measured displacement.
Figure 3 demonstrates the lung stiffness map in the same volunteer after lung density correction at RV and TLC for both optimization method and the standard DI method without any post-processing (i.e., no median filter, boundary erosion, etc.).
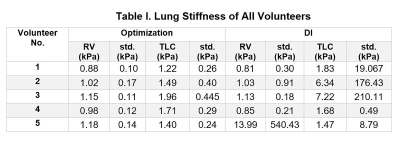
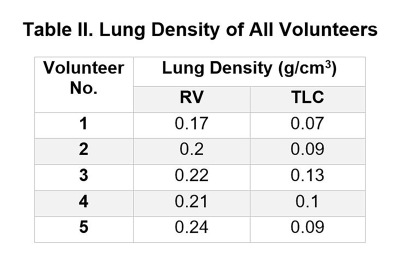
Table I summarizes the lung stiffness of each individuals. It is important to notice that the standard DI yielded unrealistic stiffness values with large standard deviation due to the noise presented in the data despite the applied 17x17 Romano filter.Table II summarizes the lung densities of each individuals.
The proposed optimization technique demonstrated significantly higher lung stiffness at TLC than RV (paired t-test, P=0.0104). The mean optimization-derived stiffness for all volunteers is 1.04±0.12 and 1.55±0.29 kPa at RV and TLC, respectively. No significant difference was observed between DI-derived RV and TLC stiffness (paired t-test, P=0.9668). The mean DI-derived stiffness for all volunteers is 3.56±5.83 and 3.71±2.82 kPa at RV and TLC, respectively.

Conclusion

In this study, the proposed optimization technique demonstrated more robust/stable stiffness estimates in the lung compared to the standard DI method, successfully demonstrating higher shear stiffness at TLC than that at RV.

Acknowledgements

The authors acknowledge grant sponsor: NIH–NHLBI (grant number: NIH-R01HL124096).

References

1. Papazoglou S, Hamhaber U, Braun J, and Sack I. Algebraic Helmholtz inversion in planar magnetic resonance elastography. Physics in medicine and biology 2008;53(12):3147-3158.

2. Oliphant TE, Manduca A, Ehman RL, and Greenleaf JF. Complex‐valued stiffness reconstruction for magnetic resonance elastography by algebraic inversion of the differential equation. Magnetic resonance in Medicine 2001;45(2): 299-310.

3. Faffe DS, Zin WA. Lung Parenchymal Mechanics in Health and Disease. Physiol Rev. 2009;89(3):759-775. doi:10.1152/physrev.00019.2007.

4. Mariappan YK, Glaser KJ, Hubmayr RD, Manduca A, Ehman RL, McGee KP. MR elastography of human lung parenchyma: Technical development, theoretical modeling and in vivo validation. J Magn Reson Imaging. 2011;33(6):1351-1361. doi:10.1002/jmri.22550.

5. McGee KP, Mariappan YK, Hubmayr RD, et al. Magnetic resonance assessment of parenchymal elasticity in normal and edematous, ventilator-injured lung. J Appl Physiol. 2012;113(4):666-676. doi:10.1152/japplphysiol.01628.2011.

6. Marinelli JP, Levin DL, Vassallo R, et al. Quantitative assessment of lung stiffness in patients with interstitial lung disease using MR elastography. J Magn Reson Imaging. 2017;46(2):365-374. doi:10.1002/jmri.25579.

7. Scherzer O. The use of Morozov’s discrepancy principle for Tikhonov regularization for solving nonlinear ill-posed problems. Computing. 1993;51:45–60.

8. Ting ST, Ahmad R, Jin N, Craft J, Serafim da Silveira J, Xue H, Simonetti OP. Fast implementation for compressive recovery of highly accelerated cardiac cine MRI using the balanced sparse model. Magnetic Resonance in Medicine 2017;77(4):1505-1515.

9. Paige CC and Saunders MA, LSQR: An Algorithm for Sparse Linear Equations And Sparse Least Squares, ACM Trans. Math. Soft. 1982;8:43-71.

10. Fakhouri F, Dong H, Kolipaka A. Magnetic resonance elastography of the lungs: A repeatability and reproducibility study. NMR Biomed. 2019. doi:10.1002/nbm.4102.

Figures

Figure 1. Flow Diagram. The acquired data are first unwrapped and filtered to obtain displacement u₀ for each direction. Subsequently, the cost function is alternatively optimized. λ₁ is controlled by a noise feedback loop (in red), allowing denoising for each direction via comparing the variance of uNoise and u-u₀. Noise ratio is second harmonic amplitude (SHA)/first harmonic amplitude (FHA) of the non-filtered data.

Figure 2. Displacement Field at Each Direction. The measured displacement u₀ and the displacement field generated from the proposed inversion were compared for each direction. Less noise was observed in the generated displacement than that in the measured displacement, demonstrating effective denoising in the lung data using the proposed technique. The real part of the complex displacement is shown in the figure.

Figure 3. Lung Stiffness Maps at RV and TLC. Lung stiffness maps at RV and TLC in the same volunteer are displayed after lung density correction. No post-processing was performed after inversion. The mean optimization-derived stiffness was 0.88±0.10 and 1.22±0.26 kPa for RV and TLC, respectively. The mean DI-derived stiffness was 0.81±0.30 and 1.83±19.07 kPa for RV and TLC, respectively. When the noise increased during TLC phase, DI showed considerably higher standard deviation.

Table I. Lung Stiffness of All Volunteers.

Table II. Lung Density of All Volunteers.

Proc. Intl. Soc. Mag. Reson. Med. 28 (2020)

3328