3324
Ultra-low frequency MR elastography of the in vivo human brain from endogenous pulsation to 40 Hz time-harmonic vibrations.1Department of Radiology, Charité Universitätsmedizin Berlin, Berlin, Germany, 2Institute of Medical Informatics, Charité Universitätsmedizin Berlin, Berlin, Germany
Synopsis
In this work, we applied single-shot steady-state MR elastography with spiral readout for quantifying shear wave speed (SWS) from endogenous pulsation to 40 Hz external vibrations with high sampling rate for first-time measurement of SWS dispersion of in vivo human brain in the ultra-low frequency regime. Ground truth SWS was determined by profile fitting approaches and reproduced by SWS mapping based on frequency-adaptive multi-component wave-number inversion. The obtained SWS dispersion was fitted by two-parameter viscoelastic models showing that brain tissue is dominated by fluid properties in this ultra-low frequency regime. Our method is potentially sensitive to vessel-related neurological disorders.
Introduction
Viscoelastic tissue properties measured at ultra-low stimulation frequencies from 1 to 10 Hz are widely unexplored in vivo1,2. We here present single-shot steady-state magnetic resonance elastography (ssMRE) of the in vivo human brain to encode harmonic tissue motion from ultra-low stimulation frequencies induced by arterial pulsation at heart rate to externally induced frequencies with overlap to the classical range of MRE frequencies between 20 and 60 Hz3,4. Covering such unprecedented wide range of frequencies ssMRE is able to measure and analyze the transition of in vivo brain tissue from its fluid-controlled poroelastic tissue response to viscoelastic dominated material properties typically measured by MRE1. This transition regime of mechanical brain properties might be particularly sensitive to neurovascular integrity and vessel-induced neurological disorders.Methods
In vivo MRE was performed in 14 healthy volunteers in compliance with our local ethics board. Phantom tests were performed in heparin-sodium gel to validate ultra-low frequency MRE against oscillatory shear rheometry6. All experiments were performed in a 1.5T MRI scanner (Siemens Magnetom Sonata, Erlangen, Germany). Three scans were consecutively acquired in each volunteer:(I) endogenously activated cerebral ssMRE (single-shot);
(II) ultra-low frequency time-harmonic ssMRE (multi-shot) with external wave stimulation at frequencies 5, 6.25, 7.8125, and 10 Hz;
(III) ssMRE (multi-shot) with externally induced waves in a conventional higher range of 20, 31.25, and 40 Hz.
We noted that a certain amount of acoustic wave energy was transmitted into the brain through higher harmonics of the fundamental driving frequency due to nonlinear actuator movement. The tissue response to these higher harmonics was also analyzed.
As ground truth, shear wave speed (SWS in m/s) was derived on the basis of profiles taken from complex-valued wave images along the wave normal. SWS was then directly be quantified by the slope of the wave front in the time-space domain.
For spatially resolved mapping of SWS, multi-component wave-number elasto-visco (k-MDEV) inversion was applied as outlined in Tzschätzsch et al.7. The spatial frequency filters were adapted to match the ground truth determined in both phantom and brain by profile fitting.
SWS dispersion curves of the phantom and in vivo brain were fitted using four models: Kelvin-Voigt, Maxwell, spring-pot, and viscous fluid yielding the parameters given in table 1.
Results
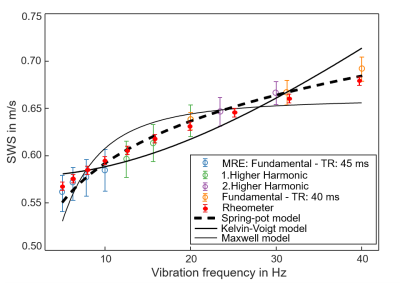
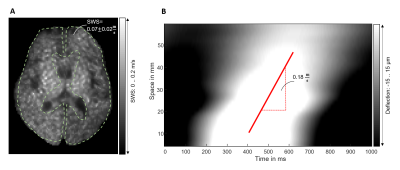
Figure 1 shows SWS dispersion of the phantom measured with shear rheometry in comparison to MRE, validating ssMRE against rheometry. Viscoelastic modelling reveals that the spring-pot model better reproduces SWS dispersion than the others, in agreement with Sauer et al.6.Figure 2 presents the findings of intrinsic activation ssMRE in a volunteer in terms of an SWS map generate d by k-MDEV inversion and by manually delineating the gradient of the wave phase in the x-t space. SWS values of k-MDEV are lower than with slope fitting (0.08±0.01m/s vs. 0.14±0.02m/s), probably because of underestimation of values by derivative gradients invoked by the k-MDEV inversion8.
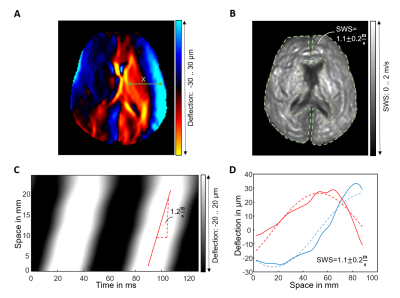
Figure 3 illustrates the methods we used to quantify SWS from harmonic wave fields at a representative frequency of 15.625 Hz. Delineation of the gradient of wave phase in the x-t space, and 1D complex wave fitting are used as ground truths for k-MDEV inversion providing similar results as inversion (1.1±0.2m/s, 1.2m/s, and 1.1±0.2 m/s, P = 0.01).
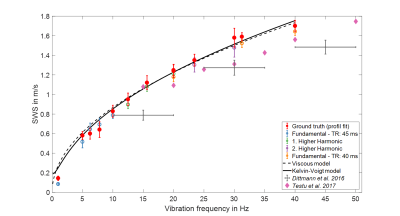
Averaged SWS values over frequency are plotted in Figure 5. Profile-based SWS recovery and k-MDEV inversion show similar dispersion functions. Fitting of rheological models to ground truth data revealed that Maxwell and spring-pot models collapse to the pure-fluid (viscous) model with η = 5.46±0.14 Pa∙s.
Discussion
Our data show for the first time that there is a continuous increase of SWS of in vivo brain from 0.1 m/s to 1.7 m/s, suggesting a viscoelastic dispersion of brain tissue similar to viscous fluids. In comparison with ground truth, we adapted noise-robust k-MDEV inversion, which has meanwhile become established for clinical abdominal MRE9. Our data in the conventional range of drive frequencies (20 to 40 Hz) fall into the range of data published in the literature10.It is an intriguing result that SWS measured with intrinsic pulsation is consistent with data obtained by extrinsic actuation when we consider the pure viscous material model. At heart rate, shear wave propagation through the multiphasic brain is enforced by fluid-filled vessels, which could explain why our SWS dispersion function reflects the behavior of materials with predominantly viscous-fluid properties.
Conclusion
We have introduced ssMRE for quantifying SWS of in vivo human brain over a large frequency range from heart rate to stimulation at 40 Hz. The validity of measurement, postprocessing, and viscoelastic model fitting was demonstrated in a gel phantom. In the brain, ssMRE could exploit cerebral arterial pulsation as a mechanical stimulus to expand the range of ultra-low frequencies for SWS quantification. Viscoelastic model fitting revealed that brain tissue is dominated by fluid properties at low frequencies.Acknowledgements
Funding from the German Research Foundation (GRK 2260 BIOQIC, SFB1340 Matrix in Vision) and from the European Union’s Horizon 2020 Program (ID 668039, EU FORCE – Imaging the Force of Cancer) is gratefully acknowledged.References
1. McGarry MD, Johnson CL, Sutton BP, et al. Suitability of poroelastic and viscoelastic mechanical models for high and low frequency MR elastography. Med Phys 2015;42(2):947.
2. Testu J, McGarry MDJ, Dittmann F, et al. Viscoelastic power law parameters of in vivo human brain estimated by MR elastography. Journal of the Mechanical Behavior of Biomedical Materials 2017;74:333-341.
3. Klatt D, Hamhaber U, Asbach P, et al. Noninvasive assessment of the rheological behavior of human organs using multifrequency MR elastography: A study of brain and liver viscoelasticity. Phys Med Biol 2007;52(24):7281–7294.
4. Sack I, Beierbach B, Wuerfel J, et al. The impact of aging and gender on brain viscoelasticity. Neuroimage 2009;46(3):652-657.
5. Weaver JB, Pattison AJ, McGarry MD, et al. Brain mechanical property measurement using MRE with intrinsic activation. Phys Med Biol 2012;57(22):7275-7287.
6. Sauer F, Oswald L, Ariza de Schellenberger A, et al. Collagen networks determine viscoelastic properties of connective tissues yet do not hinder diffusion of the aqueous solvent. Soft Matter 2019;15(14):3055-3064.
7. Tzschatzsch H, Guo J, Dittmann F, et al. Tomoelastography by multifrequency wave number recovery from time-harmonic propagating shear waves. Medical Image Analysis 2016;30:1-10.
8. Bertalan G, Guo J, Tzschatzsch H, et al. Fast tomoelastography of the mouse brain by multifrequency single-shot MR elastography. Magn Reson Med 2019;81(4):2676-2687.
9. Garcia SRM, Grossmann M, Bruns A, et al. Tomoelastography Paired With T2*Magnetic Resonance Imaging Detects Lupus Nephritis With Normal Renal Function. Investigative Radiology 2019;54(2):89-97.
10. Hiscox LV, Johnson CL, Barnhill E, et al. Magnetic resonance elastography (MRE) of the human brain: technique, findings and clinical applications. Phys Med Biol 2016;61(24):R401-R437.
11. Dittmann F, Hirsch S, Tzschatzsch H, et al. In Vivo Wideband Multifrequency MR Elastography of the Human Brain and Liver. Magnetic Resonance in Medicine 2016;76(4):1116-1126.
Figures