3321

Compartmental Low-Rank Denoising for Multi-Delay ASL

Yanis Djebra^1,2, Thibault Marin¹, Jinsong Ouyang¹, Georges El Fakhri¹, Chao Ma¹, and Paul Kyu Han¹
¹Gordon Center for Medical Imaging, Department of Radiology, Massachusetts General Hospital, Harvard Medical School, Boston, MA, United States, ²LTCI, Télécom Paris, Institut Polytechnique de Paris, Palaiseau, France

Synopsis

Arterial spin labeling (ASL) is a powerful magnetic resonance imaging (MRI) technique that allows to measure tissue perfusion, potentially an important biomarker for assessing cerebral tissue viability, without the use of contrast agent. However, the main drawback of ASL is in the intrinsically low signal-to-noise ratio (SNR). In this work, we investigate the low-rank property of ASL signal and explore the feasibility of improving the SNR of ASL signal using low-rank denoising approach. Results show that the ASL signal indeed display low-rank property and that the SNR in multi-delay ASL imaging can be improved using compartmental low-rank denoising method.

Introduction

Arterial spin labeling (ASL) is a powerful magnetic resonance imaging (MRI) technique that allows to measure tissue perfusion, potentially an important biomarker for assessing cerebral tissue viability, without the use of contrast agent^1-2. However, one of the main drawback of ASL is in the intrinsically low signal-to-noise ratio (SNR)³. Up to recently, low-rank approach has demonstrated promising results for improving the SNR in various MR applications where the signal show low-rank property^4-7. The aim of this work is to investigate the low-rank property of ASL signal and explore the feasibility of improving the SNR of ASL signal in multi-delay ASL imaging using compartmental low-rank denoising.

Methods

We performed simulation studies to investigate the low-rank properties of ASL signal. According to the standard ASL kinetic model⁸, the continuous ASL (CASL) signal can be written as:
$$\begin{align} \Delta M(t)&=0,\qquad0<t<∆t \\ \Delta M(t)&=2M_{0B}f\ T_1'\alpha\ e^{(-∆t/T_{1b})}(1-e^{-(t-∆t)/T_1'}) \qquad∆t<t<\tau+∆t \\ \Delta M(t)&=2M_{0B}f\ T_1'\alpha\ e^{(-∆t/T_{1b})}e^{-(t-\tau-∆t)/T_1'} (1-e^{-\tau/T_1'}) \qquad\tau+∆t<t\qquad (1) \end{align}$$
where $$$∆M(t)$$$ is the ASL signal, $$$M_{0B}$$$ is the equilibrium magnetization of arterial blood, $$${f}$$$ is the perfusion, $$$λ$$$ is the blood-brain partition coefficient, $$${T_1'}$$$ is the apparent relaxation time ($$$\frac{1}{T_1'}=\frac{1}{T_1}+\frac{f}{λ}$$$), $$$\alpha$$$ is the labeling efficiency, $$$∆t$$$ is the arterial transit time (ATT), $$$T_{1b}$$$ is the longitudinal relaxation time of arterial blood, and $$$\tau$$$ is the label duration. We generated simulated ASL signals in three cases: 1) $$$T_1$$$ varying from 0.5 to 3 s; 2) ATT varying from 0.1 to 2 s; and 3) both $$$T_1$$$ and ATT varying in the same range as in the previous cases. We stacked the simulated signals into 2D matrices and then performed singular values decompositions (SVD) to investigate the approximation errors with different low-rank truncations.
One healthy volunteer was imaged on a 3T whole-body scanner (Magnetom Tim Trio, Siemens Healthcare, Erlangen, Germany). The study protocol was approved by our local IRB. A three-plane localizer and a $$$T_{1}$$$-weighted magnetization-prepared rapid gradient echo (MPRAGE) (Fig.2c) scans were performed followed by a series of ASL acquisitions and a time-of-flight (TOF) MR angiography (MRA) (Fig.2d). All ASL images were acquired using pseudo-continuous ASL (pCASL)^9,10 with bSSFP readout^11,12 with recommended labeling parameters³ unless otherwise mentioned. Multi-delay ASL imaging was performed with a total of 30 post-labeling delays (PLDs) times ranging from 0.1 s to 3.0 s (with 0.1 increments) with single averaging (Fig.2a). Additional multi-delay ASL imaging was performed at 5 representative PLDs (0.7 s, 1.3 s, 1.9 s, 2.5 s and 3.0 s) with 6 averages as reference (Fig.2b). The imaging parameters of the pCASL scans were as follows: field-of-view = 256$$$\times$$$192$$$\times$$$96 mm3; matrix size = 128$$$\times$$$96$$$\times$$$24; image plane = axial; TR/TE = 3.89/1.71 ms; and flip angle = 30$$$^\circ$$$.
Image registration was performed to register the MPRAGE, MRA, and ASL images acquired at different PLDs. The registered MPRAGE image was then used for tissue segmentation using Statistical Parametric Mapping (SPM) toolbox to produce tissue masks of gray matter (GM) (Fig.3e), white matter (WM) (Fig.3f), and cerebrospinal fluid (CSF) (Fig.3g). The MRA image was thresholded to generate the blood mask (Fig.3h). The generated tissue masks were then used to collect signals from each compartments. Compartmental low-rank denoising was performed for the single-averaged multi-delay ASL data acquired at 30 PLD times via SVD decomposition and low-rank truncation using the theoretically determined rank from the simulation study. The denoised data was then compared to the original and the reference data.

Results and Discussion

Figure 1 shows the results from simulation study. The dynamics of the ASL signal were well approximated using low-rank truncation, showing 2% approximation errors with rank of 3, 6, and 6 for cases of T1 variation, ATT variation, and both T1 and ATT variations, respectively (Fig.1). Figures 3 and 4 show the results from the in vivo study. Based on the results from the simulation study, rank of 6 was used for compartmental low-rank denoising. As can be seen, the proposed method successfully reduced the noise variations in the original ASL images across different PLD times as well as different slice locations (Figs. 3 and 4). Visually, the SNR of the denoised images were comparable to those from the reference images acquired with six averages (Figs. 3 and 4). Further investigation is needed to validate the performance of the proposed denoising approach for multi-delay ASL imaging.

Conclusion

The dynamics of ASL signal show low-rank property. The SNR of ASL signal in multi-delay ASL imaging can be achieved using compartmental low-rank denoising approach.

Acknowledgements

This work was partially supported by the National Institutes of Health (P41EB022544, R01HL137230, and T32EB013180).

References

1. Detre JA, Leigh JS, Williams DS, Koretsky AP. Perfusion imaging. Magnetic resonance in medicine 1992; 23(1): 37–45.

2. Williams DS, Detre JA, Leigh JS, Koretsky AP. Magnetic resonance imaging of perfusion using spin inversion of arterial water. Proceedings of the National Academy of Sciences 1992; 89(1): 212–216.

3. Alsop, David C., et al. "Recommended implementation of arterial spin-labeled perfusion MRI for clinical applications: a consensus of the ISMRM perfusion study group and the European consortium for ASL in dementia." Magnetic resonance in medicine 73.1 (2015): 102-116.

4. Liang ZP. "Spatiotemporal imaging with partially separable functions." Biomedical Imaging: From Nano to Macro, 2007. ISBI 2007. 4th IEEE International Symposium on. IEEE, 2007.

5. Haldar, Justin P., and Zhi-Pei Liang. "Spatiotemporal imaging with partially separable functions: A matrix recovery approach." Biomedical Imaging: From Nano to Macro, 2010 IEEE International Symposium on. IEEE, 2010.

6. Zhao B et al. "Image reconstruction from highly undersampled-space data with joint partial separability and sparsity constraints." IEEE transactions on medical imaging 31.9 (2012): 1809-1820.

7. J. He et al. "Accelerated High-Dimensional MR Imaging With Sparse Sampling Using Low-Rank Tensors," IEEE transactions on medical imaging, vol. 35, pp. 2119-29, Sep 2016.

8. Buxton, R. B., Frank, L. R., Wong, E. C., Siewert, B. , Warach, S. and Edelman, R. R. (1998), A general kinetic model for quantitative perfusion imaging with arterial spin labeling. Magn. Reson. Med., 40: 383-396.

9. Wu WC, Fernández-Seara M, Detre JA, Wehrli FW, Wang J. A theoretical and experimental investigation of the tagging efficiency of pseudocontinuous arterial spin labeling. Magnetic Resonance in Medicine: An Official Journal of the International Society for Magnetic Resonance in Medicine 2007; 58(5): 1020–1027

10. Dai W, Garcia D, De Bazelaire C, Alsop DC. Continuous flow-driven inversion for arterial spin labeling using pulsed radio frequency and gradient fields. Magnetic Resonance in Medicine: An Official Journal of the International Society for Magnetic Resonance in Medicine 2008; 60(6): 1488–1497.

11. Park SH, Wang DJ, Duong TQ. Balanced steady state free precession for arterial spin labeling MRI: initial experience for blood flow mapping in human brain, retina, and kidney. Magnetic resonance imaging 2013; 31(7): 1044–1050

12. Han PK, Ye JC, Kim EY, Choi SH, Park SH. Whole-brain perfusion imaging with balanced steady-state free precession arterial spin labeling. NMR in biomedicine 2016; 29(3): 264–274.

Figures

Figure 1. Simulation results. The first column shows ASL signal changes as functions of $$$T_{1}$$$, ATT, and both. The second column plots the corresponding singular value decays, showing that 2% approximation errors can be achieved with only rank 6. The last column shows the low-rank approximated signal variations (dot lines) and confirm the small approximation error predicted in the second column. (Parameter used for the plots: $$$\tau$$$= 1.5 s; $$$T_{1b}$$$= 1.8 s; $$$\lambda$$$ = 0.9; $$$f$$$ = 0.01 $$$s^{-1}$$$.)

Figure 2. Illustration of the structural and functional images acquired in the multi-delay ASL experiment. (a) Low-SNR multi-delay ASL images with single average and 30 PLDs ranging from 0.1 s to 3 s (increments of 0.1 s). (b) Reference multi-delay ASL data with six averages at 5 representative PLD times of 0.7 s, 1.3 s, 1.9 s, 2.5 s, and 3 s. (c) MPRAGE images used for generating GM, WM and CSF masks shown in (e) to (g). (d) MRA images used for generating blood mask is in (h).

Figure 3. Denoising results of the proposed method at representative PLDs. As can be seen, the proposed method successfully reduced the noise variations in the original ASL images. The image quality of the denoised images is visually comparable to the reference images acquired with six averages.

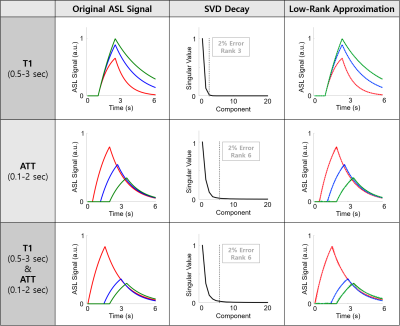
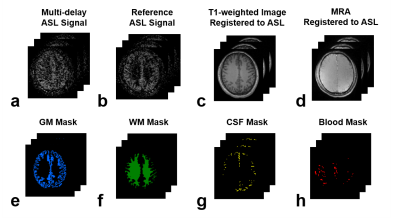
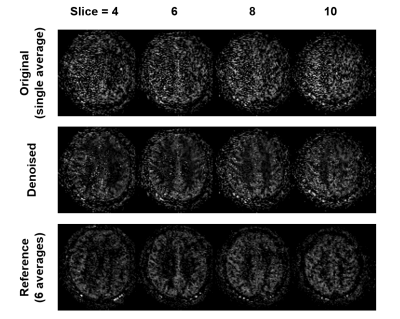
Figure 4. Denoising results of the proposed method across different slice locations. The same denoising results as in Figure 3 but at different slices for PLD = 1.5 s to further illustrate the performance of the proposed method.

Proc. Intl. Soc. Mag. Reson. Med. 28 (2020)

3321