3310

Joint Elasticity Reconstruction and Displacement Filtering for 3D Magnetic Resonance Elastography

Shahed Khan Mohammed¹, Mohammad Honarvar¹, Davood Karimi¹, Piotr Kozlowski^2,3, and Septimiu Salcudean¹
¹Electrical and Computer Engineering, University of British Columbia, Vancouver, BC, Canada, ²UBC MRI Research Center, Vancouver, BC, Canada, ³Department of Radiology, University of British Columbia, Vancouver, BC, Canada

Synopsis

Iterative reconstruction methods in magnetic resonance elastography (MRE) inversion can allow incorporating sparsity prior and can provide displacement filtering. However the problem is difficult to converge as MRE inversion is a non-convex and ill-conditioned problem. Here, we presented 3D ERBA with total variation prior on the elasticity, which showed good convergence by utilizing a bi-convex optimization of 3D finite element modeling of elastic wave. Extensive experiments on numerical phantom, agar phantom, and in-vivo liver study showed promising indications in detecting inclusion and abnormality, and improving the diagnostic efficacy of MRE.

Introduction

Model-based iterative reconstruction (MBIR) with sparsity prior has been shown to improve low dose CT¹and compressed sensing MRI² reconstructions, with better resolution, contrast, and robustness to noise. However, MBIR performs poorly in Magnetic Resonance Elastography (MRE), because the inversion problem is non-convex and ill-conditioned^3,4. Currently, two-dimensional direct inversion methods with local homogeneity and plane stress assumptions are widely used, even though their performance is strongly dependent on data quality^5,6. A 2D iterative method, Elasticity Reconstruction with Bi-convex Alternating direction method of multipliers (ERBA) was recently presented and showed good convergence with robustness to initialization and displacement noise⁷. This study aims to extend 2D ERBA to 3D. 3D ERBA uses a finite element model and 3D total variation regularization to increase the resolution, contrast and accuracy of MRE.

Theory

The governing equations for a linear, isotropic, and viscoelastic medium subjected to the time-harmonic motion of frequency $$$\omega$$$ can be modelled as a system of the shear modulus $$$\mu$$$ and displacement $$$\mathbf{u}$$$ with the following formulation⁸:

$$\nabla \cdot \left[ \mu \left( \nabla \mathbf{u} + \left( \nabla \mathbf{u} \right)^T \right) \right]= \rho \omega^2 {\mathbf{u}}$$

where $$$\rho$$$ is the density of the medium. Using finite element modelling under the incompressible assumption, the system can be transformed to a bi-affine system of the shear modulus $$$\mu$$$ and displacement $$$\mathbf{u}$$$ without the local homogeneity assumption in the following form:
$$\mathbb{A}(\mu,\mathbf{u})= \left[ \mathbf{K} \left( \mu\right)-\omega^2 \mathbf{M}\right] \, \mathbf{u}= \mathbf{0}$$
Here, $$$\mathbf{K}$$$ is the stiffness matrix and $$$\mathbf{M}$$$ is the mass matrix. The operator $$$\mathbb{A}(\mu,\mathbf{u})$$$, representing the FEM system with variables $$$\mu$$$ and $$$\mathbf{u}$$$, is bi-affine⁷. The model based iterative reconstruction with a 3D total variation regularization can be represented by the following constrained optimization problem, with convex cost and bi-affine constraint:
$$\left(\mu, \mathbf{u}\right) =arg \underset{\begin{subarray}{c} \mu, \mathbf{u}\\ \end{subarray}}{\min} \,\,\,\Bigg\{\frac{1}{2} || \mathbf{u}-\mathbf{v}||^2+\gamma ||\mu||_{TV} \Bigg\} \\ \mbox{ subject to} \begin{array}{cl} \mathbb{A}\left(\mathbf{u}, \mu\right)= \mathbf{0} \\\end{array}$$

Methods

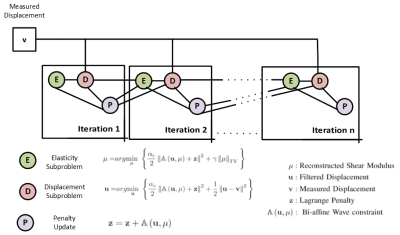
Reconstruction Algorithm: The bi-affine optimization problem was solved using the Alternating Direction Method of Multipliers (ADMM)⁹, which separates the problem into three sub-problems (Fig. 1). All the regularization parameters were optimized using a grid search on a synthetic dataset. We validated the proposed method in simulations, phantoms and human subjects.

Simulated Liver Data: For our simulations, the shape of the liver was taken from the manual segmentation of a subject’s T2W liver image. The segmented mask was transformed into a triangulated surface mask, which was imported to COMSOL Multiphysics software. Two spherical shaped inclusions with elasticity of 12 KPa (hard) and 100Pa (soft) were placed inside the simulated liver. The liver elasticity and viscosity was chosen as 4KPa and 5.5 Pa-s respectively. Shear waves at 60Hz were simulated in the frequency domain using the displacement boundary constraint, where a prescribed displacement was imposed on the right side of the liver, while the remainder was taken as free.

Image Acquisition: 3D MRE was performed on an agar phantom with a vibration frequency of 300 Hz. The agar phantom had irregular shape inclusions which were made by introducing a high concentration solution to a low concentration background solution¹⁰. We also present reconstruction results from in-vivo liver data from volunteer scans taken at 60 Hz with a Lorentz coil shaker and GRE exPresso Sequence¹¹. MRE imaging parameters included: TE= 6.9 ms, 300 x 300 mm2 FOV; 176 x 176 reconstruction matrix; 8 slices; 4 dynamics.

Results and Discussion

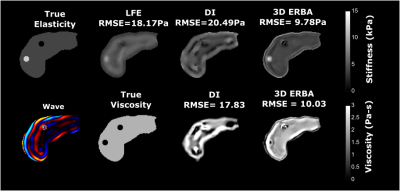
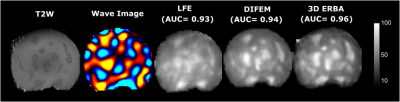
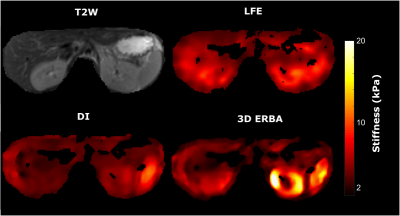
A finite element Direct Inversion (DI) method⁷ and the Local Frequency Estimation (LFE)⁶ were implemented. Reconstructions results show an overestimation of background elasticity and underestimation of inclusion elasticity (Fig 2), while 3D ERBA provides the closest value to the true elasticity value. In the reconstructed viscosity map by both DI and 3D ERBA, some boundary artifacts can be clearly seen leading to an error in the inclusion viscosity. However, 3D ERBA can better distinguish between the inclusion and the background.
For the agar phantom, we have used a bandpass filtering in the range of 1kPa- 120kPa to eliminate measurement noise and dilatational waves¹². We see similar results to simulation, where the 3D ERBA provided the best area under the curve (AUC) score for differentiating between the background and the inclusion (Fig 3). The increased AUC stems from the better performance of 3D ERBA with smaller inclusions, as both LFE and DI underestimate the elasticity in such a case. Moreover, the 3D TV prior allows generating crisp edges for the inclusions while reducing the intra-class variation. Results from a healthy volunteer and patient with cirrhosis show that the proposed method provides more anatomical detail of the abdomen scan, where the liver, the kidney and the spleen can be easily distinguished (Fig 4. and Fig 5). The increase in stiffness due to cirrhosis is clearly visible in LFE and 3D ERBA.

Conclusion

We extend our work on 2D iterative elasticity reconstruction to 3D MRE by utilizing an ADMM based method with a 3D total variation prior. The reconstructed results show higher resolution and accuracy compared to DI and LFE. These promising results warrant investigation on the clinical significance of the reconstructed elasticity. Therefore, future investigation would focus on multi-frequency reconstruction method and finding the correlation with histopathology data.

Acknowledgements

This work was funded by NSERC, CIHR and the Charles Laszlo Chair in Biomedical Engineering held by Professor Salcudean.

References

[1] Geyer, L.L., Schoepf, U.J., Meinel, F.G., Nance Jr, J.W., Bastarrika, G., Leipsic, J.A., Paul, N.S., Rengo, M., Laghi, A. and De Cecco, C.N., 2015. State of the art: iterative CT reconstruction techniques. Radiology, 276(2), pp.339-357.

[2] Quan, T.M., Nguyen-Duc, T. and Jeong, W.K., 2018. Compressed sensing MRI reconstruction using a generative adversarial network with a cyclic loss. IEEE transactions on medical imaging, 37(6), pp.1488-1497.

[3] Otesteanu, C. F., Sanabria, S. J., & Goksel, O. (2018). Robust Reconstruction of Elasticity Using Ultrasound Imaging and Multi-frequency Excitations. IEEE Transactions on Medical Imaging, 37(11), 2502–2513.

[4] Honarvar, M., Rohling, R., & Salcudean, S. E. (2016). A comparison of direct and iterative finite element inversion techniques in dynamic elastography. Physics in Medicine and Biology, 61(8), 3026–3048. https://doi.org/10.1088/0031-9155/61/8/3026.

[5] Tzschatzsch, H., Guo, J., Dittmann, F., Hirsch, S., Barnhill, E., Johrens, K.,Sack, I. (2016). Tomoelastography by multifrequency wave number recovery from time-harmonic propagating shear waves. Medical Image Analysis, 30, 1–10.

[6] Manduca, A., Muthupillai, R., Rossman, P. J., Greenleaf, J. F., & Ehman, R. L. (1996). Image Processing for Magnetic Resonance Elastography. Proc. of SPIE’s Intern. Symposium Medical Imaging, 2710, 616–623.

[7] Mohammed, S., Honarvar, M., Kozlowski, P., & Salcudean, S. E. (2019). 2D ELASTICITY RECONSTRUCTION WITH BI-CONVEX ALTERNATING DIRECTION METHOD OF MULTIPLIERS In 2019 IEEE 16th International Symposium on Biomedical Imaging (ISBI 2019) (pp. 1683–1687). IEEE.

[8] Honarvar, M., Sahebjavaher, R. S., Salcudean, S. E., & Rohling, R. (2012). Sparsity regularization in dynamic elastography. Physics in Medicine and Biology, 57, 5909–5927.

[9] Boyd, S., Parikh, N., Chu, E., Peleato, B., & Eckstein, J. (2010). Distributed Optimization and Statistical Learning via the Alternating Direction Method of Multipliers. Foundations and Trends in Machine Learning, 3(1), 1–122.

[10] Honarvar, M., Sahebjavaher, R., Rohling, R., & Salcudean, S. (2017). A comparison of FEM-based inversion algorithms, Local frequency estimation and direct inversion approach used in MR elastography. IEEE Transactions on Medical Imaging, 0062(c).

[11] Sahebjavaher, R. S., Frew, S., Bylinskii, A., ter Beek, L., Garteiser, P., Honarvar, M.,Salcudean, S. (2014). Prostate MR elastography with transperineal electromagnetic actuation and a fast fractionally encoded steady-state gradient echo sequence. NMR in Biomedicine, 27(7), 784–794.

[12] Barnhill, E., Hollis, L., Sack, I., Braun, J., Hoskins, P. R., Pankaj, P., … Roberts, N. (2017). Nonlinear multiscale regularisation in MR elastography: Towards fine feature mapping. Medical Image Analysis, 35, 133–145. https://doi.org/10.1016/j.media.2016.05.012

Figures

The proposed method solves the bi-convex elasticity optimization problem by iteratively solving three subproblems. The first (E) solves for elasticity given displacements, the second (D) solves for displacements given elasticity, through regularized least squares that includes a Lagrange penalty z that penalizes any deviation from the wave constraint A(u,mu)=0.

Validation of proposed method in a viscoelastic simulation of a segmented liver. The liver is modeled as a homogeneous viscoelastic medium with Young’s modulus of 4 kPa and viscosity of 5.5 Pa-s. Two 10mm spherical inclusions with elasticities of 12 kPa and 100 Pa and zero viscosity are placed in the liver. The proposed method 3D ERBA gives the best result for both elasticity and viscosity.

Stiffness results from an agar phantom with irregular shaped inclusion shows that 3D ERBA provides the best Area under the curve (AUC) for a linear classifier from the reconstructed elasticity map. The ground truth was segmented from the T2W image. Thus 3D ERBA provides better detection performance.

Stiffness results from a healthy volunteer. The displacement was captured at a voxel size of 1.73 mm at a slice thickness of 5mm. During pre processing, displacements were interpolated to isotropic voxel size of 2mm in all dimensions, and the fat layer and bones were masked out using manual segmentation. Both LFE and DI used a bandpass filtering of 1kPa-20kPa for displacement denoising. Our proposed 3D ERBA does not use a pre-processing bandpass filtering, except median filtering to remove high-frequency noise.

Stiffness results from a patient diagnosed with Cirrhosis. Compared to the healthy volunteer, the increase in stiffness is visible in both LFE and 3D ERBA.

Proc. Intl. Soc. Mag. Reson. Med. 28 (2020)

3310