Introduction

Fourier-transform based velocity-selective inversion (FT-VSI) prepared arterial spin labeling (ASL) has demonstrated improved SNR for brain perfusion mapping¹. Although paired and phase-cycled refocusing pulses improved its robustness to B0 and B1 inhomogeneities, severe B0/B1 offsets are known to cause imperfect refocusing leading to stripe artifacts in velocity-selective MR angiography^2,3. In ASL, the periodic banding of high spatial-frequency is averaged out due to low spatial resolution. Instead, net DC-bias subtraction errors for perfusion quantification was newly identified in the current study, especially when applying the control modules with gradients turned off as often adopted in VSASL. Here a new dynamic phase-cycling scheme is proposed to mitigate the DC-bias for VSI-ASL and is evaluated in simulations, phantom and human brain scans at 3T.

Methods

Numerical simulation was conducted using Matlab. A 64ms FT-VSI pulse train was composed of nine excitation pulses and eight 8ms velocity-encoding steps, each containing paired and phase-cycled composite refocusing pulses⁴ and four triangular gradient lobes (30mT/m, 0.6ms duration, 0.3ms ramp, 2cm/s cut-off velocity). Both Mz-velocity and Mz-position responses were evaluated for three schemes: 1) using velocity-insensitive control with gradients turned off; 2) using velocity-compensated control with uni-polar gradient lobes^3-5) using velocity-insensitive control while phase-cycling the refocusing pulses of every label/control pairs by 90° through every four dynamics (dynamic 1: +0°; dynamic 2: +90°; dynamic 3: +180° and dynamic 4: +270°) in addition to the MLEV-16 phase-cycling applied within the VS pulse trains. The label/control subtraction results of phase-cycled dynamics are averaged to yield the final image.
Experiments on an oil phantom and five healthy volunteers (two females, 32 ± 5 yo) were performed on a 3T Siemens Prisma scanner. VSI-ASL sequences with schemes 2 and 3 were implemented as described above. B1+ scale were manually adjusted to 0.8, 1.0 and 1.2. A six-segment 3D gradient- and spin-echo (GRASE) readout was applied with: imaging volume=220x220x96mm³, resolution=3.4x3.4x4.0mm³, reconstructed to 1.7x1.7x4.0mm³. Post-labeling delays (PLD) was 0.1s for phantom scans and 1.5s for brains. Four dynamics were acquired in around 2min for phantom and 3.3min for brain scans. For phantom scans, the subtraction results between label/control pairs were divided by M0. For brain scans cerebral blood flow (CBF) of whole-brain gray matter (GM) were calculated. Student’s paired t-test was used to evaluate signal difference.

Results

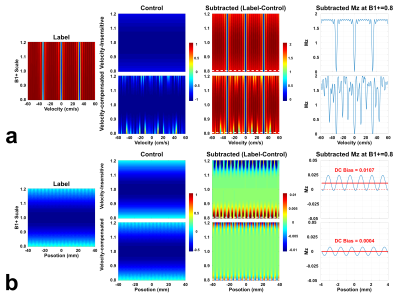
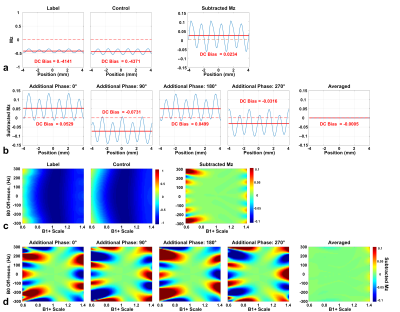
Simulated Mz-velocity and Mz-position responses for both velocity-insensitive and velocity-compensated controls (schemes 1 and 2) with varied B1+ were shown in Fig.1. The subtracted signal of scheme 1 showed well-maintained velocity-selective profiles, except labeling efficiency scaled by B1. The velocity-selective profile of scheme 2 is more susceptible to B1+ imperfection (Fig.1a). However, Mz-position responses showed less stripes and DC-bias (average of stripes) in scheme 2 as the velocity-compensated control largely cancels this effect (Fig.1b), as observed experimentally before^2,4,5.
In a specific B0/B1 condition (B0=150Hz and B1+=0.7) as example, the subtraction of label and control of scheme 2 yielded much reduced banding and DC bias (Fig.2a) than scheme 1. Scheme 3 with averaging through dynamic phase-cycling further suppressed artifacts (Fig.2b). When DC bias is plotted as functions of B0/B1 (Fig.2c,d), similar performance are shown. The false perfusion signal was considerably canceled with scheme 3 within a wide range of B0/B1.
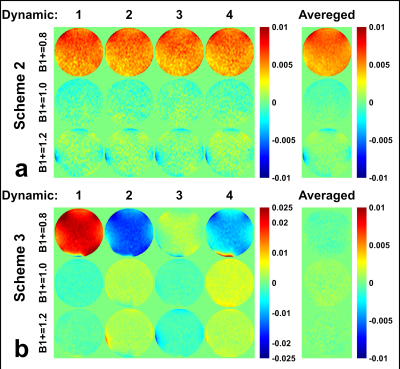
The normalized subtraction results of phantom scans at three B1+ scales were shown with all four dynamics and their averages in Fig.3. For scheme 2, a strong positive false signal were present with B1+ of 0.8. Some negative false signal can also be seen at the edge of the phantom with B1+ of 1.2, probably due to a combined B1 and B0 imperfections. For scheme 3, although each dynamic generated strong false signal, they were mostly canceled after averaging.
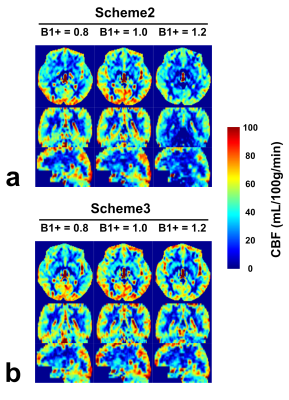
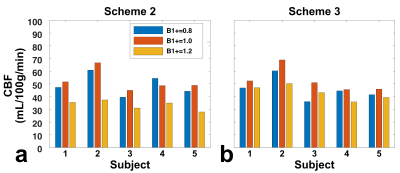
Similar effects were observed for brain CBF mapping (Fig.4). Note that for scheme 2, B1+ of 0.8 showed a stronger signal than 1.2, although with the same theoretical labeling efficiency. This asymmetry was likely caused by different false signal with B1+ of 0.8 and 1.2 in scheme 2 (Fig.3a). In contrast, scheme 3 after averaging the dynamic phase-cycles showed consistent CBF results.
The whole-brain GM CBF was displayed for all five subjects (fig.5). The asymmetry of B1+ of 0.8 and 1.2 was significant in scheme 2 (p=0.004), but not in scheme 3 (p=0.431). Interestingly, with scheme 2, B1+ of 1.2 showed significantly lower perfusion signal (p=0.012) than the results with scheme 3, which could not be explained by false signal alone. This was attributed to the loss of labeling efficiency in scheme 2 due to poor B1+ (Fig.1a). In principle, B1+ of 0.8 in scheme 2 should have similar effect, but the lower perfusion signal was likely counteracted by the strong positive false signal observed in phantom experiments (Fig.3a).

Conclusion

In this VSI ASL study, we proposed dynamic phase-cycling scheme for the FT-VS label and control modules while using velocity-insensitive controls in order to achieve high labeling efficiency in the presence of a wide range of B0/B1 field inhomogeneities. Simulation, phantom scans, and brain perfusion measurements all demonstrated considerable improvement with our proposed method.

Acknowledgements

No acknowledgement found.