3296

Low-Rank Reconstruction for Multi-Delay Arterial Spin Labeling

Paul Kyu Han¹, Yanis Djebra^1,2, Thibault Marin¹, Georges El Fakhri¹, Jinsong Ouyang¹, and Chao Ma¹
¹Radiology, Massachusetts General Hospital and Harvard Medical School, Boston, MA, United States, ²LTCI, Télécom Paris, Institut Polytechnique de Paris, Palaiseau, France

Synopsis

Multi-delay arterial spin labeling (ASL) is a powerful MRI technique that allows to non-invasively measure both cerebral blood flow and arterial transit time quantitatively, which has great potential for clinical applications. However, usage of multi-delay ASL is limited by the prolonged scan time with the number of post-labeling delay times used for acquisition. Up to date, low-rank property has been observed in signals of various MR applications where low-rank approach has demonstrated promising results. This work shows that the dynamics of ASL signal display low-rank property and the scan time of multi-delay ASL can be accelerated using low-rank image reconstruction.

Introduction

Multi-delay arterial spin labeling (ASL) is a powerful MRI technique that allows to non-invasively measure both cerebral blood flow (CBF) and arterial transit time (ATT) quantitatively^1-4. Recent study indicates that employing large number of PLDs can be optimal for accurate estimation of CBF and ATT⁵. However, the imaging time of multi-delay ASL can be impractical for large number of PLDs due to the intrinsically low signal-to-noise ratio (SNR) and less efficient data acquisition scheme in ASL imaging (i.e., long TRs). This work presents a subspace-based imaging method to accelerate the imaging speed of multi-delay ASL imaging. Our method exploits a unique property of high-dimensional MR signals, known as partial separability (PS), for sparse-sampling and image reconstruction^6-9. A special data acquisition and image reconstruction method is proposed to recover multi-delay ASL images from highly under-sampled k-space data. The performance of our proposed method is validated using in vivo study.

Methods

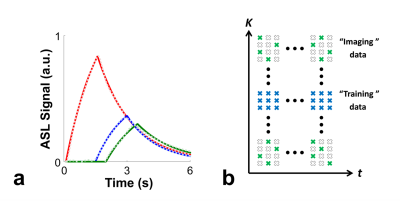
The low-rank property of ASL signal was investigated via a simulation study. Variations of ASL signal dynamics were simulated using the standard ASL kinetic model for pseudo-continuous ASL (pCASL)¹⁰ with a range of T₁ (from 0.5 s to 3 s) and ATT values (from 0.1 s to 2 s) and all other parameters fixed at recommended setting¹¹. Results showed that all ASL signal dynamics from different combinations of T₁ and ATT can be approximated well with 2% and 1% error using rank of 6 and 7 of SVD decomposition, respectively. Figure 1a shows representative results of ASL signal dynamics along with the low-rank approximation (rank=6) for three different cases of T₁ and ATT values.
The image function of multi-delay ASL signal $$$\rho(x,t)$$$ is modeled as PS functions^6-9:
$$\rho(x,t) = \sum_{l=1}^{L} U_{l}(x)V_{l}(t) (1)$$
where $$$x$$$, $$$t$$$, and $$$L$$$ denote the spatial dimension, PLD time, and model order, respectively. The proposed model indicates that the imaging function resides in a low-dimensional subspace. Our preliminary investigation shows that it is sufficient to estimate $$$V_{l}(t)$$$ using fully-sampled data from a limited number of locations at the k-space center (Fig. 1b). All other k-space locations can be sparsely-sampled over the entire $$$(k,t)$$$-space as long as sufficient number of measurements (larger than the model order $$$L$$$) are sampled for each location for image reconstruction (Fig. 1b).
With estimated temporal basis functions $$$\hat{V}_{l}(t)$$$, the spatial coefficients $$$ U_{l}(x)$$$ can be determined by solving the following optimization problem:
$$\underset{U}{\operatorname{argmin}}||F \{\sum_{l=1}^{L}U_{l}(x) \hat{V}_{l}(t)\} – d(k,t)||_2^2 + R(\{U_{l}(x)\}) (2) $$
where $$$d(k,t)$$$ denotes the sparsely-sampled k-space data of multi-delay ASL, $$$F$$$ denotes the forward model taking sparse-sampling, coil sensitivity and Fourier transform into account, and R(·) denotes an edge-preserving regularization penalty⁷.
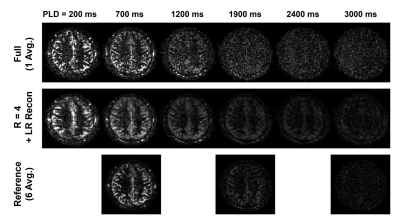
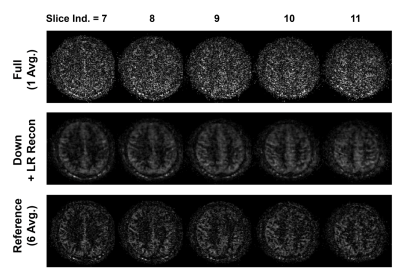
An in vivo experiment was performed to show the feasibility of the proposed method. One healthy volunteer was imaged using a 3T Siemens Trio MR scanner (approved by our local Institutional Review Board). ASL imaging was performed using pCASL^12-13 with 3D bSSFP readout^14-15 with conventional labeling parameters¹¹ and imaging parameters similar to previous study¹⁵. General imaging parameters were: image plane=axial; matrix size=128$$$\times$$$96$$$\times$$$24; voxel size=2$$$\times$$$2$$$\times$$$4 mm³; TR/TE=3.89/1.71 ms; flip angle=30$$$^\circ$$$; acquisition bandwidth=592 Hz/pixel; and TR time of control/label unit=5.5 s. Multi-delay ASL imaging was examined at three different settings: full-sampling of single-average ASL acquisitions at 30 PLD times (PLD times ranging from 100 ms to 3000 ms with increments of 100 ms, scan time per PLD acquisitions=1.3 min), under-sampling of single-average ASL acquisitions at 30 PLD times with acceleration factor (r) of 4, and full-sampling of six-average acquisitions at 5 PLD times (PLD times of 700 ms, 1300 ms, 1900 ms, 2500 ms, and 3000 ms, scan time per PLD acquisitions=5.3 min) as reference. A separate scan without labeling was acquired for M0. The center 16$$$\times$$$8 of k-space phase-encoding lines were used to estimate the temporal basis functions and the coil sensitivity maps for SENSE¹⁶-based low-rank reconstruction. CBF was estimated for each voxel using the multi-delay ASL data via least-square fitting to the standard ASL kinetic model¹⁰ using variable projection algorithm¹⁷.

Results and Discussion

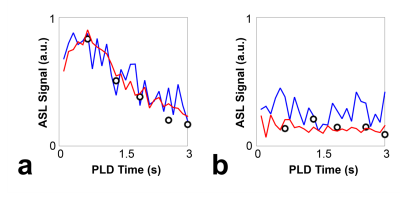
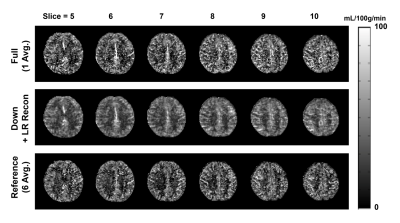
Overall, the proposed low-rank approach successfully reconstructed the 3D image in multi-delay ASL imaging with down-sampling (Figures 2 and 3). The reconstructed multi-delay ASL signal showed improved SNR, comparable to the 6-average reference scan (Figures 2, 3 and 4). Blurring of ASL signal was also observed in the reconstructed ASL images within voxels containing blood vessel at early PLD times, which is presumed to be due to the T1-weighted image showing enhanced gray matter and white matter contrast difference without blood vessel information used as anatomical prior for image reconstruction (Figure 2). Noticeable signal bias was observed in the reconstructed ASL signal in gray matter regions from acquisitions at later PLD times (e.g., PLD time>2.5 s) compared to the reference scan (Figure 4), which is presumed to have affected the estimation of the CBF (Figure 5). Further investigation is necessary with more subjects to validate and accurately assess the performance of the proposed method.

Conclusion

The dynamics of ASL signal display low-rank property. The scan time of multi-delay ASL imaging can be accelerated using the proposed method.

Acknowledgements

This work was partially supported by the National Institutes of Health (P41EB022544, R01HL137230, and T32EB013180).

References

1. Dai, Weiying, et al. "Reduced resolution transit delay prescan for quantitative continuous arterial spin labeling perfusion imaging." Magnetic resonance in medicine 67.5 (2012): 1252-1265.

2. Wang, Danny JJ, et al. "Multi-delay multi-parametric arterial spin-labeled perfusion MRI in acute ischemic stroke—comparison with dynamic susceptibility contrast enhanced perfusion imaging." NeuroImage: Clinical 3 (2013): 1-7.

3. Fan, Audrey P., et al. "Long-delay arterial spin labeling provides more accurate cerebral blood flow measurements in moyamoya patients: a simultaneous positron emission tomography/MRI study." Stroke 48.9 (2017): 2441-2449.

4. Choi, H. J., et al. "Can arterial spin-labeling with multiple postlabeling delays predict cerebrovascular reserve?." American Journal of Neuroradiology 39.1 (2018): 84-90.

5. Woods, Joseph G., Michael A. Chappell, and Thomas W. Okell. "A general framework for optimizing arterial spin labeling MRI experiments." Magnetic resonance in medicine 81.4 (2019): 2474-2488.

6. Liang ZP. "Spatiotemporal imaging with partially separable functions." Biomedical Imaging: From Nano to Macro, 2007. ISBI 2007. 4th IEEE International Symposium on. IEEE, 2007.

7. Haldar, Justin P., and Zhi-Pei Liang. "Spatiotemporal imaging with partially separable functions: A matrix recovery approach." Biomedical Imaging: From Nano to Macro, 2010 IEEE International Symposium on. IEEE, 2010.

8. Zhao B et al. "Image reconstruction from highly undersampled-space data with joint partial separability and sparsity constraints." IEEE transactions on medical imaging 31.9 (2012): 1809-1820.

9. J. He et al. "Accelerated High-Dimensional MR Imaging With Sparse Sampling Using Low-Rank Tensors," IEEE transactions on medical imaging, vol. 35, pp. 2119-29, Sep 2016.

10. Buxton, Richard B., et al. "A general kinetic model for quantitative perfusion imaging with arterial spin labeling." Magnetic resonance in medicine 40.3 (1998): 383-396.

11. Alsop, David C., et al. "Recommended implementation of arterial spin-labeled perfusion MRI for clinical applications: a consensus of the ISMRM perfusion study group and the European consortium for ASL in dementia." Magnetic resonance in medicine 73.1 (2015): 102-116.

12. Dai, Weiying, et al. "Continuous flow-driven inversion for arterial spin labeling using pulsed radio frequency and gradient fields." Magnetic Resonance in Medicine: An Official Journal of the International Society for Magnetic Resonance in Medicine 60.6 (2008): 1488-1497.

13. Wu, Wen-Chau, et al. "A theoretical and experimental investigation of the tagging efficiency of pseudocontinuous arterial spin labeling." Magnetic Resonance in Medicine: An Official Journal of the International Society for Magnetic Resonance in Medicine 58.5 (2007): 1020-1027.

14. Park, Sung-Hong, Danny JJ Wang, and Timothy Q. Duong. "Balanced steady state free precession for arterial spin labeling MRI: initial experience for blood flow mapping in human brain, retina, and kidney." Magnetic resonance imaging 31.7 (2013): 1044-1050.

15. Han, Paul Kyu, et al. "Whole-brain perfusion imaging with balanced steady-state free precession arterial spin labeling." NMR in biomedicine 29.3 (2016): 264-274.

16. Pruessmann, Klaas P., et al. "SENSE: sensitivity encoding for fast MRI." Magnetic resonance in medicine 42.5 (1999): 952-962.

17. Golub, Gene et al. "Separable nonlinear least squares: the variable projection method and its applications." Inverse Problems 19.2 (2003): R1.

Figures

Figure 1. Low Rank Property of ASL Signal. a: Simulation of ASL signal dynamics from a variation of T₁ (ranging from 0.5 s to 3 s) and ATT values (ranging from 0.1 s to 2 s). Representative ASL dynamics curves (solid line) along with the low-rank approximation (rank=6) (dotted line) are shown for T₁ and ATT values corresponding to blood (red line), gray matter (blue line), and white matter (green line). b: Proposed acquisition scheme consisting of fully-sampled “training” dataset for estimation of the temporal bases and sparsely-sampled “imaging” dataset for image reconstruction.

Figure 2. Low-rank reconstruction of multi-delay ASL signal. ASL subtraction map from fully-sampled single-average data, down-sampled (r=4) single-average data with low-rank reconstruction, and reference 6-average scan are shown at representative post-labeling delay (PLD) times.

Figure 3. Low-rank reconstruction of ASL signal over multiple slice regions. ASL subtraction map from fully-sampled single-average data, down-sampled (r=4) single-average data with low-rank reconstruction, and reference 6-average scan are shown over representative slice regions for the case of post-labeling delay (PLD) time of 1900 ms.

Figure 4. Comparison of signal dynamics of ASL subtraction signal. a: ASL subtraction signal dynamics from the gray matter region for fully-sampled single-average data (blue line), down-sampled (r=4) single-average data with low-rank reconstruction (red line), and reference 6-average scan (black circle) are shown. b: ASL subtraction signal dynamics from the white matter region for fully-sampled single average data (blue line), down-sampled (r=4) single-average data with low-rank reconstruction (red line), and reference 6-average scan (black circle) are shown.

Figure 5. CBF mapping result. CBF map estimated from fully-sampled single average data, down-sampled single-average data with low-rank reconstruction, and reference 6-average scan are shown.

Proc. Intl. Soc. Mag. Reson. Med. 28 (2020)

3296