3290
Robust Perfusion Parameter Quantification from 3D Single-Shot Multi-Delay ASL measurements1Institute of Medical Engineering, Graz University of Technology, Graz, Austria, 2Deptartment of General Neurology, Medical University of Graz, Graz, Austria, 3Application Development, Siemens Healthcare, Erlangen, Germany, 4Biotechmed, Graz, Austria
Synopsis
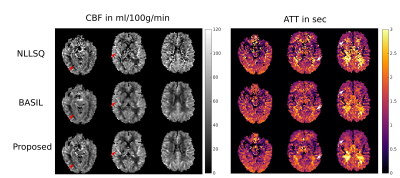
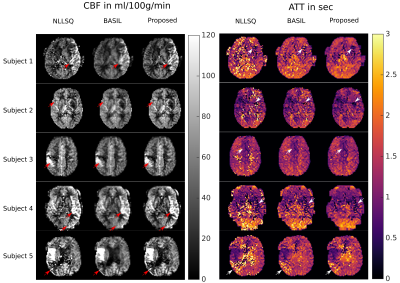
Multi-Delay single-shot ASL imaging provides accurate CBF and, in addition, ATT maps but the inherent low SNR can be challenging. State-of-the-art fitting techniques can improve the SNR in the estimated maps but typically suffer from spatial blurring. To this end, we propose a new reconstruction method with a joint TGV regularization on CBF and ATT to reconstruct sharp maps with improved noise suppression. Validation of the proposed method on a healthy subject and five stroke patients showed preservation of even small features in CBF and ATT while increasing SNR and sharpness over recent approaches.
Introduction
Multi-Delay Arterial Spin Labeling (ASL) has been shown to be highly beneficial in elderly subjects, patients with prolonged arterial transit time, or cerebrovascular disease1. It provides more accurate cerebral blood flow (CBF) maps and, in addition, the arterial transit time (ATT) which is helpful in characterization or detection of cerebrovascular diseases. Current ASL imaging employs segmented 3D data acquisition due to efficient background suppression and SNR gains1. To achieve appropriate temporal resolution and motion robustness an accelerated single shot acquisition is required2,3,4 but the inherent low SNR of the perfusion weighted time series makes the estimation of CBF and ATT challenging. Current approaches use either voxel-wise non-linear least squares (NLLSQ) fitting or a weighted delay approach5 leading to outliers in low-SNR voxels. Inclusion of spatial priors on the CBF map6 in a Bayesian inference model (BASIL7) stabilizes the fitting approach and leads to improved CBF-maps but introduces blurring. Exploiting all available spatial information by means of a joint regularization strategy on all unknowns can further improve reconstruction quality and has been successfully applied in the context of relaxometry8,9. Joint regularization utilizes information present in each map, such as tissue boundaries, to avoid the loss of small features and leading to overall sharper parameter maps. To this end, we propose a new model based fitting algorithm with joint spatial constrains on the CBF and ATT map to further improve the estimation procedure. The proposed method is validated on one healthy subject as well as on five stroke patients and compared to NLLSQ and BASIL. The results showed improved stability of the fitting procedure with less outliers and an enhanced contrast-to-noise ratio in CBF and ATT maps. In addition, previously invisible hypoperfusion areas in the ATT map are revealed.Methods
The present work is based on a recently published parameter quantification algorithm8 utilizing a joint regularization strategy on both unknowns. As parameter quantification typically deals with non-linear fitting problems we can adapt the idea to fit the signal intensity values to the general ASL perfusion model for pCASL labeling7 given by:$$\Delta M(CBF,ATT)_t=\begin{cases}0&t<ATT\\2M_{0a}\alpha CBF\,T_{1app}e^{-\frac{ATT}{T_{1b}}}\left(1-e^{-\frac{t-ATT}{T_{1app}}}\right)&ATT\leq t<ATT+\tau \\2M_{0a}\alpha CBF\,T_{1app}e^{-\frac{ATT}{T_{1b}}}e^{-\frac{t-ATT-\tau}{T_{1app}}}\left(1-e^{-\frac{\tau}{T_{1app}}}\right)&ATT+\tau \leq t\end{cases}$$
where $$$1/T_{1app} = {1/T_1+CBF/\lambda}$$$, $$$M_{0a}=M0/\lambda$$$. $$$T_1$$$ is the relaxation decay of the tissue, $$$M_0$$$ the acquired proton density weighted image and $$$T_b$$$ the relaxation decay of blood. $$$\tau$$$ corresponds to the labeling duration and $$$\alpha$$$ to the labeling efficiency. The optimization problem solved takes on the following form:
$$
\underset{x=(CBF, ATT)}{\min}\,\,\frac{1}{2}\|\Delta M(x)-y\|_2^2+\lambda{TGV}(x)
$$
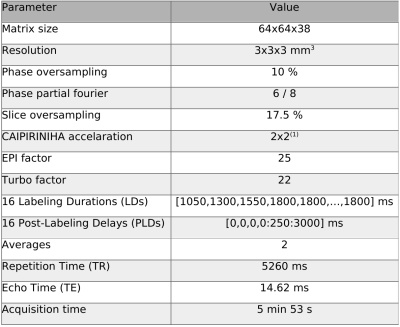
consisting of a data-fidelity term and a joint Total-Generalize-Variation (TGV)8,11,12 constrained on CBF and ATT. Jointly regularizing preserves fine structures which could be otherwise wrongly classified as noise. As the problem at hand is non-linear we make use of the iteratively-regularized Gauss-Newton algorithm to solve for CBF and ATT8. One healthy volunteer and five patients were scanned at a 3T MR system (Prisma, Siemens Healthcare, Germany) following the local ethic guidelines. To reduce the motion sensitivity, we performed a single shot prototype pCASL sequence with a 2D-CAIPIRINHA accelerated 3D-GRASE readout using the imaging parameters given in Table 1. The position of the labeling plane was guided by an additional TOF scan. Prior to fitting the ASL images were motion-corrected using ASL-Toolbox13, SPM1214,15 (Wellcome Trust Centre for Neuroimaging, University College London, UK), and Matlab (MathWorks, Natick, MA, USA). The proposed method was compared to a NLLSQ fitting procedure with positivity constraints on the CBF and ATT implemented in Matlab as well as the BASIL fitting approach7.
Results and Discussion
In order to increase motion robustness and the number of temporal sampling points a single-shot acquisition was used. This leads to a reduction of SNR and manifests in distinct noise corruption of the corresponding parameter maps for the NLLSQ method (Figure 1). The BASIL approach shows superior noise suppression at the cost of spatial blurring (Figure 1). In contrast, the proposed joint regularization enhances image sharpness while maintaining the noise suppression property. Thus, small features and tissue boundaries in CBF and ATT are easily distinguishable from noise (red/white arrows in Figure 1 and 2). Hypoperfusion regions can be easily distinguished in both, CBF and ATT maps, using the joint regularization approach. In contrast, the reference methods generally show higher noise levels in the corresponding ATT areas (Figure 2). The regularization parameters were optimized on the healthy subject and applied to all patients without further modification. The strength of the regularization is automatically adapted according to the estimated SNR in the data. The proposed method is easily applicable to different SNR cases and imaging parameters, opposed to common deep learning techniques. The fitting procedure of the full volume takes approximately 4 minutes on a NVIDIA GTX 1080 TI using OpenCL and Python.Conclusion
We have shown that the proposed fitting method with joint regularization on CBF and ATT enables detection of hypoperfusion regions in the ATT map. Additionally the parameter maps are sharper with fewer outliers compared to the reference methods. The proposed model is easily extendable to three or four parameter fits including the estimation of the arterial blood volume or $$$T_1$$$ of the tissue. In addition, raw k-space data could be directly fitted to the parameters to allow for further undersampling of k-space.Acknowledgements
Oliver Maier is a Recipient of a DOC Fellowship (24966) of the Austrian Academy of Sciences at the Institute for Medical Engineering at TUGraz.
NVIDIA Corporation Hardware grant support.
References
1. Alsop DC, Detre JA, Golay X, et al. Recommended implementation of arterial spin-labeled perfusion MRI for clinical applications: A consensus of the ISMRM perfusion study group and the European consortium for ASL in dementia. Magn. Reson. Med. 2015:73:102–116.
2. Ivanov D, Pfeuffer J, Gardumi A, et al. 2D CAIPIRINHA improves accelerated 3D GRASE ASL. In Proceedings of the 25th Annual Meeting of ISMRM, Honolulu, 2017
3. Spann SM, Shao X, Wang DJJ et al. Improving temporal resolution of 3D Arterial Spin Labeling perfusion imaging by combining CAIPIRINHA encoding and spatiotemporal TGV reconstruction, In Proceedings of the 27th Annual Meeting of ISMRM, Montreal, 2019
4. Boland M, Stirnberg R, Pracht ED, et al. Accelerated 3D-GRASE imaging improves quantitative multiple post labeling delay arterial spin labeling. Mag. Reson. Med. 26 (2018)
5. Dai W, Robson PM, Shankaranarayanan A, Alsop DC. Reduced resolution transit delay prescan for quantitative continuous arterial spin labeling perfusion imaging. Magn. Reson. Med. 2012;67:1252–1265. doi: 10.1002/mrm.23103.
6. Groves AR, Chappell MA, Woolrich MW. Combined spatial and non-spatial prior for inference on MRI time-series. Neuroimage 2009;45:795–809. doi: 10.1016/j.neuroimage.2008.12.027.
7. Chappell MA, MacIntosh BJ, Donahue MJ, et al. Separation of macrovascular signal in multi-inversion time arterial spin labelling MRI. Magn Reson Med. 2010;63(5):1357-1365.
8. Maier O, Schoormans J, Schloegl M, Strijkers GJ, Lesch A, Benkert T, Block T, Coolen BF, Bredies K, Stollberger R. Rapid T 1 quantification from high resolution 3D data with model‐based reconstruction. Magn. Reson. Med. 2019;81:2072–2089. doi: 10.1002/mrm.27502.
9. Wang X, Roeloffs V, Klosowski J, Tan Z, Voit D, Uecker M, Frahm J. Model-based T 1 mapping with sparsity constraints using single-shot inversion-recovery radial FLASH. Magn. Reson. Med. 2018;79:730–740. doi: 10.1002/mrm.26726.
10. Buxton RB, Frank LR, Wong EC, et al. A general kinetic model for quantitative perfusion imaging with arterial spin labeling. Magn. Reson. Med. 1998;40(3):383–396.
11. Bredies K, Kunisch K, Pock T. Total Generalized Variation. SIAM J. Imaging Sci. 2010;3:492–526. doi: 10.1137/090769521.
12. Knoll F, Bredies K, Pock T, Stollberger R. Second order total generalized variation (TGV) for MRI. Magn. Reson. Med. 2011;65:480–491. doi: 10.1002/mrm.22595.
13. Friston K, Ashburner J, Kiebel S, Nichols T, Penny W eds. Statistical Parametric Mapping. Elsevier/Academic Press; 2007. doi: 10.1016/B978-0-12-372560-8.X5000-1.
14. Wang Z. Improving cerebral blood flow quantification for arterial spin labeled perfusion MRI by removing residual motion artifacts and global signal fluctuations. Magn. Reson. Imaging 2012;30:1409–1415. doi: 10.1016/j.mri.2012.05.004.
15. Wang Z, Aguirre GK, Rao H, Wang J, Fernández-Seara MA, Childress AR, Detre JA. Empirical optimization of ASL data analysis using an ASL data processing toolbox: ASLtbx. Magn. Reson. Imaging 2008;26:261–269. doi: 10.1016/j.mri.2007.07.003.
Figures