Introduction

Imperfect labeling impairs the accuracy of CBF quantification from pCASL. Reduced labeling efficiency occurs due to off-resonance near regions of increased susceptibility, tortuous vessels, and velocity variation in blood flow ^1,2. While label plane locations can be prescribed based on an additional angiogram, the choice of labeling plane location is heuristically optimized and does not generally consider flow, B1+ uniformity, or off-resonance. As such, it is common to place the labeling plane at a fixed location (e.g. 85mm below the anterior commissure-posterior commissure line³) resulting in label efficiency variations across populations. Here, we propose a multi-distance and orientation labeling plane pCASL protocol combined with a method for CBF mapping estimation robust to poor labeling.

Methods

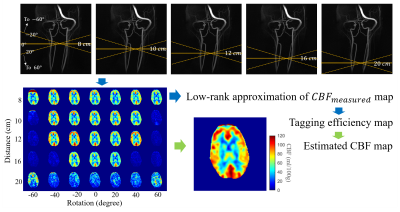
pCASL data in five healthy volunteers were acquired using a 3.0T scanner (Signa Premier, GE Healthcare) using a 48-channel head coil (GE Healthcare) with the labeling plane shifted and rotated about the A/P axis of the scanner (Figure 1). Imaging parameters included: post-label delay=2s, 4-shot 3D spiral sampling, single average. The labeling plane was rotated from -60 $$$^{\circ}$$$ to 60 $$$^{\circ}$$$ in 20 $$$^{\circ}$$$ increments and also translated along the S/I axis with distances 8, 10, 12, 16 and 20 cm from the lower edge of pCASL FOV. The goal of moderate shifts and rotations was to allow for optimal labeling in each individual while more extreme parameters were used for simulating poor labeling and to demonstrate robustness of image combination techniques. Data was also collected in volunteers in the neck tilted up and down state to simulate labeling variability incurred in patient population. The labeling plane for the tilt-neck experiments was rotated from 0 to 60 $$$^{\circ}$$$ at fixed distance of 10 cm. T1 weighted and 4D flow images were acquired for registration and visualization purposes as anatomical reference.
Assuming a symmetric, zero mean noise distribution, the CBF was estimated using least-squares and a pixelwise solution: $$$ (\bf{\alpha}^{H}\bf{\alpha})^{-1}\bf{\alpha}^{H} \bullet CBF_{measured} $$$ , where $$$\bf{\alpha}$$$ is a spatial variant tagging efficiency map. Typically, $$$\alpha$$$ is assumed to be global and constant but in reality, it is dependent on the feeding vessel. Since the blood supply of the brain comes from only a few arteries, it is reasonable to assume the spatial distribution of can be estimated by the low-rank approximation of $$$ CBF_{measured} $$$. Singular value decomposition of $$$ CBF_{measured, full} $$$, which is measured CBF maps acquired from different angles concatenated to a number-of-pixels² by number-of-rotations matrix. The low-rank approximation was done by taking the leading singular values and vectors $$$U_{r}S_{r}V^{T}_{r}$$$, where r is the rank used. In this work we used $$$r=2$$$ considering left/right asymmetry. It is then reshaped back to a square matrix. The entries of this square matrix were normalized to the maximum value of that pixel in the entire case (through all distances and rotations), which corresponds to an ideal labeling plane for that pixel with a theoretically maximum labeling efficiency. This yields relative tagging efficiency maps for each rotation, each slice and $$$CBF_{recovered} = \sum^{rotations} \frac{\bf{\alpha}^{H}CBF_{measured\,at\,each\, rotation}}{\bf{\alpha}^{H}\bf{\alpha}}$$$. The low-rank projection preserves spatial resolution compared to other neighborhood-based efficiency estimation techniques. For comparison, global tagging efficiency , which was calculated by taking the ratio of total brain CBF measured with each labeling plane to the “ideal” labeling plane ($$$ CBF_{measured,max} $$$), was also used to estimate true CBF, which was a weighted sum of measured CBF map with weights $$$ (\alpha_{global}^{H} \alpha_{global})^{-1} \alpha_{global}^{H} $$$.

Results

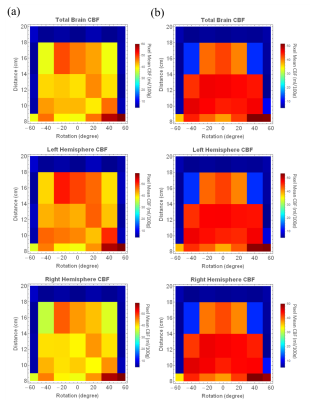
Figure
2 shows the relative tagging
efficiency varies significantly with labeling plane shift/rotation. Noticed that for all
volunteers, optimal labeling plane was not the default plane(10 cm
below FOV). Partially-tagged
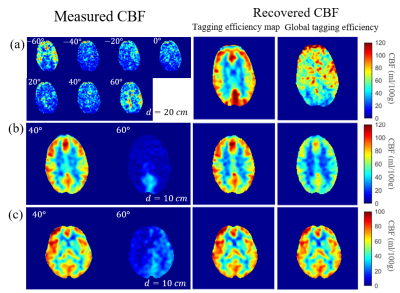
artifacts and signal dropout are demonstrated in Figure 3, along with corresponding
recovered CBF maps with tagging efficiency map $$$\bf{\alpha}$$$ and $$$\alpha_{global}$$$ . Figure 3(a) comes from the acquisition described in Figure 1. When tagging efficiency maps were estimated for each rotation,
each distance by solving pixelwise least-square problem and pixelwise
normalization, the recovered CBF maps from uninterpretable measured series were
accurate when comparing to other labeling locations in Figure 1. However, using $$$\alpha_{global}$$$ did not yield satisfying
results. Figure
3(b) and (c) were recovered from neck-tilting experiments with
two different labeling planes: 40 and 60 $$$^{\circ}$$$ using both $$$\bf{\alpha}$$$ maps and $$$\alpha_{global}$$$. Since in these two
cases, one of the labeling planes is sufficient, can also recover parts of
the CBF map but still showed poor quantification.

Discussion and conclusions

By adding addition locations and rotations to the labeling plane and solving least-square problem with low-rank estimated tagging-efficiency map, we were able to recover true CBF from $$$CBF_{measured} $$$. We artificially created tagging artifacts by using radical shift, rotation and changing neck orientations and proved true CBF can be estimated rather accurately. Tagging artifacts are more common in clinical settings due to pathology and torturous anatomy, which can makes ASL images uninterpretable ^4,5. Therefore, we believe our method could improve the reliability of ASL to quantify perfusion clinically. More studies are needed in clinical populations to evaluate this. The main limitation of our current protocol is increased scan time. Acceleration techniques are under investigation including using parallel imaging with temporal constrained reconstruction or single shot spiral trajectory ⁶.

Acknowledgements

We gratefully acknowledge research support from GE Healthcare.