3212

Sampling and Modeling UTE Signals is Important to Estimate Bone Marrow Susceptibility

Christof Böhm¹, Sophia Kronthaler¹, Maximilian N. Diefenbach^1,2, Jakob Meineke³, and Dimitrios C. Karampinos¹
¹TUM, Munich, Germany, ²Division of Infectious Diseases and Tropical Medicine, University Hospital, LMU, Division, Munich, Germany, ³Philips Research, Hamburg, Germany

Synopsis

Body QSM relies on accurate magnetic field-mapping. A well-established water–fat voxel signal model with shared $$$R_2^*$$$ has successfully been used for body QSM based on multi-echo data at conventional echo times. However, when UTE echoes are recorded to obtain field-map information in previously unavailable MR signal voids, such as trabecular bone, the above water–fat model is no longer accurate. Therefore a joint 2-signal-model fitting using graph-cuts is proposed and applied. Further, this work demonstrates the importance of UTE echoes to obtain correct susceptibility values of cortical bone and more importantly, for bone marrow.

Purpose

The non-invasive measurement of bone density is strongly relevant in the assessment of osteoporotic fracture risk¹. Quantitative susceptibility mapping (QSM) has been proposed for measuring bone density due to the diamagnetic properties of the trabecular bone matrix^2,3,4. Previous reports on bone QSM include susceptibility measurements for trabecularized bone marrow using conventional echo times (TE)^2,3and for cortical-bone using ultra-short echo times (UTE). Not accounting for the signal from the cortical-bone shell around the bone marrow might affect the bone marrow susceptibility estimation, especially next to cortical-bone surfaces perpendicular to the main magnetic field $$$B_0$$$⁵. To recover the signal from the cortical-bone UTE need to be acquired. Using both UTE and conventional TE, the analysis of multiecho gradient echo data requires the appropriate signal modeling⁷ and should account for different the T2* decay effects between cortical-bone and other tissues⁶. Here, we develop a signal model for analyzing multiecho data acquired at both UTE and conventional TE and characterize the importance of recovering signal from cortical-bone regions using UTE for bone marrow QSM.

Methods

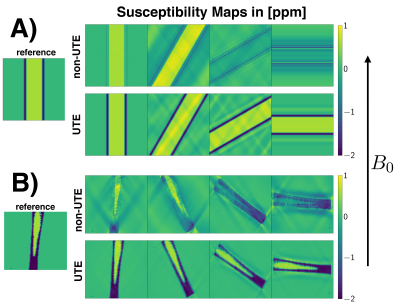
Simulation
To investigate the importance of UTE in bone-QSM, a simulation of a numerical hollow-cylinder-phantom and a simulation based on an in-vivo cortical-bone structure were set-up. The cylinder was homogeniously assigned with a diamagnetic susceptibility value of $$$-2\:$$$ppm. Within the hollow cylinder the susceptibility was set to $$$0.6\:$$$ppm to mimic bone marrow susceptibility. The susceptibility of the hollow-cylinder was forward-simulated for different angles with respect to $$$B_0$$$ to a field-map by convolution with the dipole-kernel in $$$k$$$-space. The field-map was inverted to a susceptibility-map using the closed-form $$$\ell_2$$$-regularized dipole inversion method. To simulate the difference between UTE and non-UTE field-map information, the inversion was performed once with known field-map values on the cylinder and once with these values set to zero. A second more realistic simulation was set-up by segmenting the cortical-bone structure of the femur of an in-vivo scan and the above pipeline was similarly applied.
In-vivo measurements
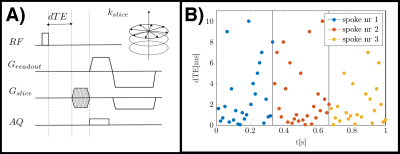
One scan of a femur of a healthy volunteer was performed on a 3$$$\:$$$T scanner (Ingenia/Philips Healthcare/Best/Netherlands). A 3D-UTE sequence was used with stack-of-stars center-out radial acquisition and phase-encoding in the third cartesian dimension. After the non-selective hard-pulse a variable delay was introduced before the start of the readout. All TEs of one spoke were acquired before the spoke was rotated and the order of the TEs was randomized⁹as depicted in Fig.1. The imaging parameters were set to TE$$$=0.19,0.24,0.34,0.54,0.74,1.29,2.39,3.49,4.59,5.69,6.79$$$ms, orientation=axial, FOV=$$$155\times{155}\times{210}\:$$$mm$$$^3$$$ and acquisition voxel size =$$$1.4\times{1.4}\times{1.5}\:$$$mm$$$^3$$$, SENSE-factor:R=2.
Signal Modeling
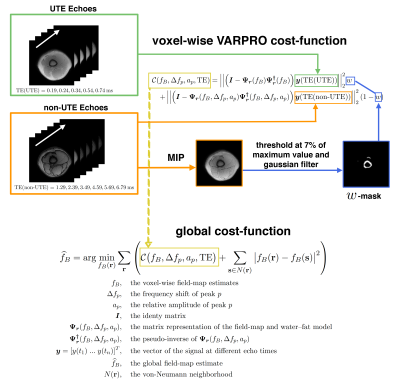
First, field-mapping was performed using a single-min-cut graph-cut algorithm^10,11 and a voxelwise method¹². A non-UTE field-map was created using the above mentioned graph-cut with only the later echoes of the acquisition (TE$$$=1.29,2.39,3.49,4.59,5.69,6.79\:$$$ms) and a fat spectrum with 10 spectral peaks specific to bone marrow¹³. Second, field-mapping was performed accounting for the different signal behaviour of UTE echoes using the signal model proposed in⁷ for UTE cortical-bone imaging. Third, a VARPRO formulation is proposed to perform the $$$w$$$-weighted voxel-wise fitting using different signal models for different TE ranges, resulting in a cost function depending on the field-map term only. For cortical-bone regions a single component with a $$$R_2^*$$$(cortical) decay is fitted to the UTE data (TE$$$=0.19,0.24,0.34,0.54,0.74\:$$$ms), for the rest of the volume a multi-compartment fat spectrum with a spectrum specific to bone marrow is fitted to the non-UTE TE (TE$$$=1.29,2.39,3.49,4.59,5.69,6.79\:$$$ms). All cost function values are calculated over a range of $$$[-600, 600]\:$$$Hz. Local minima are extracted and put into a global cost-function imposing spatial smoothness on the field-map: This cost-function is solved using graph-cuts similar to^10,11,14. The pipeline of the proposed UTE field-mapping method is depicted in Fig.3.
In-vivo QSM processing
For the in-vivo QSM pipeline the background field removal method Laplacian boundary value (LBV)¹⁵ was used. For the field-to-susceptibility inversion the following $$$\ell_1$$$-regularized cost-function was minimized:$$\chi(\mathbf{r})=\underset{\chi'}{\arg\min}\big|\big|\text{w}(f_{B}-d*\chi')\big|\big|_2^2+\lambda\big|\big|\nabla\chi'\big|\big|_1,$$where the maximum intensity projection over TEs was set as the weighting factor w, $$$d$$$ is the dipole-kernel and the regularization factor $$$\lambda=0.003$$$ for data-sets and field-maps.

Results

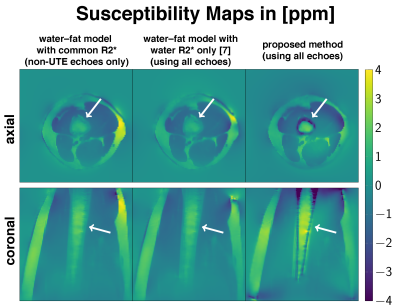
Fig.1 shows the estimation the susceptibility distribution within a perfect cylinder up to a certain angulation with respect to $$$B_0$$$. However, in a realistic hollow-cylinder cortical-bone model enclosing bone marrow it is not possible to homogeniously estimate the bone marrow susceptibility for any angulation with non-UTE field-map information. Only the proposed field-mapping method using both the UTE and conventional TEs is able to correctly pickup the diamagnetic nature of cortical-bone and subsequently improve the susceptibility estimation of the bone marrow, shown in Fig.4+5.

Discussion & Conclusion

UTE is important to correctly estimate susceptibility values of cortical-bone and the enclosed bone marrow. The simulations of a realistic cortical-bone structure emphasizes the need for UTE even when the hollow cylinder structure is aligned with $$$B_0$$$ to correctly estimate the susceptibility of the enclosed bone marrow. In a in-vivo scan only the proposed field-mapping method applied into a dataset including both UTE and conventional TEs was able to reveal the true underlying diamagnetic nature of cortical-bone. However, the proposed method has the limitation that regions of cortical-bone need to be identified in a masking step to apply the simultaneous weighted 2-model voxel-wise fitting.

Acknowledgements

The present work was supported by the European Research Council (grant agreement No 677661, Pro- FatMRI). This work reflects only the authors view and the EU is not responsible for any use that may be made of the information it contains. The authors acknowledge finally research support from Philips Healthcare.

References

[1] Wehrli FW, Song HK, Saha PK, Wright AC. Quantitative mri for the assessment of bone structure and function. NMR in Biomedicine 2006; 19:731–764.

[2] Diefenbach MN, Meineke J, Ruschke S, Baum T, Gersing A, Karampinos DC. On the sensitivity of quantitative susceptibility mapping for measuring trabecular bone density. Magnetic Resonance in Medicine 2018; .

[3] Bray TJ, Karsa A, Bainbridge A, Sakai N, Punwani S, HallCraggs MA, Shmueli K. Association of bone mineral density and fat fraction with magnetic susceptibility in inflamed trabecular bone. Magnetic Resonance in Medicine 2019; 81:3094–3107.

[4] Jerban S, Lu X, Jang H, Ma Y, Namiranian B, Le N, Li Y, Chang EY, Du J. Significant correlations between human cortical bone mineral density and quantitative susceptibility mapping (qsm) obtained with 3d cones ultrashort echo time magnetic resonance imaging (ute-mri). Magnetic Resonance Imaging 2019; 62:104–110.

[5] Böhm C, Diefenbach MN, Meineke J, Karampinos DC. Estimating Magnetic Susceptibility Within a Hollow Cylinder and its Implications in Body QSM. In: 5th International Workshop on MRI Phase Contrast & QSM, Seoul, Korea, 2019. p. 26.

[6] Du J, Bydder GM. Qualitative and quantitative ultrashort-te mri of cortical bone. NMR in Biomedicine 2012; 26:489–506.

[7] Dimov AV, Liu Z, Spincemaille P, Prince MR, Du J, Wang Y. Bone quantitative susceptibility mapping using a chemical species-specific r2* signal model with ultrashort and conventional echo data. Magnetic Resonance in Medicine 2017; 79:121–128.

[8] Bilgic B, Chatnuntawech I, Fan AP, Setsompop K, Cauley SF, Wald LL, Adalsteinsson E. Fast image reconstruction with l2-regularization. Journal of Magnetic Resonance Imaging 2013; 40:181–191.

[9] Boucneau T, Cao P, Tang S, Han M, Xu D, Henry RG, Larson PEZ. In vivo characterization of brain ultrashort-t2 components. Magnetic Resonance in Medicine 2017; 80:726–735.

[10] Böhm C, Diefenbach MN, Haase A, Karampinos DC. Accelerated Single-Min-Cut Graph-Cut Algorithm Using a Variable-Layer Graph Construction Improves Field-Mapping in Water–Fat Regions. In: Proceedings 27. Annual Meeting International Society for Magnetic Resonance in Medicine, Montreal, Canada, 2019. p. 4007. Digital Poster.

[11] Böhm C, Diefenbach MN, Meineke J, Haase A, Karampinos DC. Improved Body Quantitative Susceptibility Mapping by Using a Variable-Layer Single-Min-Cut Graph-Cut Algorithm for Field-Mapping. In: Proceedings 27. Annual Meeting International Society for Magnetic Resonance in Medicine, Montreal, Canada, 2019. p. 0693. Oral presentation, Magna cum laude merit award.

[12] Diefenbach MN, Ruschke S, Karampinos DC. A generalized formulation for parameter estimation in mr signals of multiple chemical species. In: Proceedings 25. Annual Meeting International Society for Magnetic Resonance in Medicine, Honolulu, Hawaii, 2017. p. 5181. Electronic poster presentation.

[13] Ren J, Dimitrov I, Sherry AD, Malloy CR. Composition of adipose tissue and marrow fat in humans by1h nmr at 7 tesla. Journal of Lipid Research 2008; 49:2055–2062.

[14] Shah A, Bai J, Abramoff MD, Wu X. Optimal multiple surface segmentation with convex priors in irregularly sampled space. CoRR 2016; .

[15] Zhou D, Liu T, Spincemaille P, Wang Y. Background field removal by solving the laplacian boundary value problem. NMR in Biomedicine 2014; 27:312–319.

Figures

Figure 1: Numerical simulation of (A) an annular bone structure and (B) a realistic cortical bone structure inclosing bone marrow at different angles with respect to the $$$B_0$$$. When the bone field-map information is unknown (non-UTE), the susceptibility values inside the bone can be retrieved when the cylinder is aligned with $$$B_0$$$ field in (A) but never in (B). When the bone field-map is known (UTE) the susceptibility values inside and outside the bone can be estimated for each angle in both A and B.

Figure 2: 3D UTE stack-of-stars acquisition: A) After the excitation the FID readout starts after a variable delay dTE and the duration of a slice encoding gradient, B) All TEs along one spoke are acquired in a random order before the readout of the next spoke. Points of the same color belong to the same spoke and the order of three successive acquired spokes are shown.

Figure 3: Depiction of the proposed UTE field-mapping pipeline. The echoes are separated into UTE and non-UTE echoes. From the non-UTE echoes the $$$w$$$-mask is derived indicating regions with UTE signal. Subsequently a VARPRO-based voxel-wise cost function calculated for a range for field-map values $$$f_B$$$ assuming different signal models for UTE and non-UTE signal regions. All found local minima in $$$\mathcal{C}$$$ are ultimately put into a global cost-function imposing spatial smoothness on the field-map. The global costfunction is solved via a graph-cut.

Figure 4: Comparison of field-mapping results of an in-vivo scan of the femur for different water–fat signal models. The proposed method yields a significantly different field-map on the cortical bone. Furthermore, the overall appearance of the field-map is more homogeneous especially in the bone marrow. The method proposed in (7) for cortical bone imaging yields similar results as conventional echo time field-mapping on the cortical bone.

Figure 5: Comparison of susceptibility maps of an in-vivo scan of the femur for different water–fat signal models. Only the proposed method is able to pick up the diamagnetic nature of the cortical bone, while the method proposed in (7) and non-UTE QSM falsely indicates the cortical bone to be paramagnetic.

Proc. Intl. Soc. Mag. Reson. Med. 28 (2020)

3212