Introduction

In the context of the 5th International Workshop on Phase Contrast and Quantitative Susceptibility Mapping (2019, Seoul, Korea) the QSM Challenge 2.0 was carried out. [CM1] Puedes meter un par de oraciones mas que den la motivacion/necesidad del challenge. Participants were asked to submit reconstructions of synthetic phase data. Two datasets were provided, based on simulated multiecho acquisitions¹. The main difference between both datasets is the presence of an intra-hemispheric calcification and different levels of susceptibility contrast between tissues. The first stage of the challenge involved the submission of results without access to the ground-truth. Our submission using a novel mixing of L1-norm and L2-norm data fidelity terms in the QSM functional was awarded as winner in the "Lowest RMSE" category for this first stage. Our hybrid method (unpublished) is based on a novel L1-norm reconstruction² and the L2-norm methods available in the FANSI Toolbox³. Here we present an analysis of the QSM Challenge 2.0 data and results, along with a proof of concept in one in vivo dataset to validate our method with clinical settings.

Methods

Our method consists of two independent iterative steps. The first step is to find suitable initial solution, robust to artefacts. This is done by solving the functional $$$\min_{\chi_1}‖w(F^H DFχ_1-ϕ)‖_1 +λ_1⋅TV(χ_1 )$$$ where $$$‖‖_1$$$ is the L1-norm, $$$F$$$ denotes the Fourier transform, $$$F^H$$$ is the inverse Fourier transform, the diagonal matrix $$$D=(1/3-(k_z^2)/k^2 )$$$ the dipole kernel, $$$\phi$$$ is tissue phase, $$$w$$$ is a spatially variable weight defined as: $$$w=(\sum_{i=1}^n Mag_i^2⋅TE_i)/(\sum_{I=1}^n Mag_i⋅TE_i)$$$ and $$$\lambda_1$$$ is the regularization parameter. The second step is to solve the linear L2-norm functional, using the solution of the previous step as the initialization, $$$\min_{χ_2} 1/2⋅‖ω(F^H DFχ_2-ϕ)‖_2^2+λ_2⋅TV(χ_2 )$$$ where $$$ω=w⋅(1-|ϕ-F^H DFχ_1 |/(\max |ϕ-F^H DFχ_1 |))$$$ is the corrected data fidelity weight by the discrepancy map between first step solution and input local phase map. We solved these optimization problems using ADMM. ADMM introduce one regularization parameter for each functional, $$$mu_1$$$ and $$$\mu_2$$$. The number of iterations in each step, $$$i_1$$$ and $$$i_2$$$, are additional free parameters. For simplicity we set the following heuristic: $$$i_1=20$$$, $$$i_2=280$$$, $$$\lambda_1 = \sqrt{\lambda_2}$$$, $$$\mu_1 = \sqrt{\mu_2}$$$, $$$\mu_2 = p \cdot \lambda_2$$$. For the challenge we used $$$p=10$$$ and for the in vivo data we used $$$p=100$$$.
To validate this method we performed the following experiments:

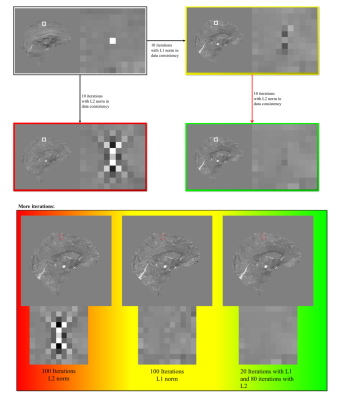
1. A) QSM Challenge 2.0 dataset⁴. We included a single-voxel phase jump to test robustness against streaking artifacts. We analyzed the effects of the initialization in the L2-norm method. We also analyzed the solutions produced by the L1-norm and L2-norm and the hybrid methods.
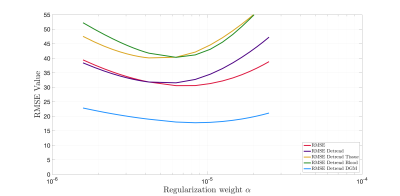
2. B) Analysis of the sensitivity of the parameters in QSM challenge 2.0 data. We obtained the optimal regularization weights by minimization of the RMSE metric and analyzed all error metrics in a range of one order of magnitude around the optimal, for reconstructions with our hybrid method.
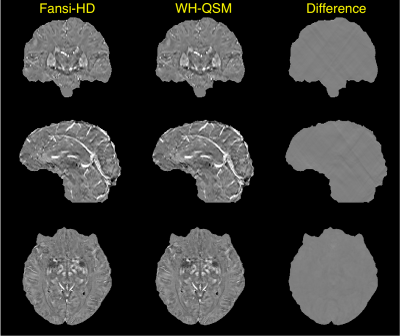
3. C) In vivo reconstructions, Phillips Ingenia 3T. TGE sequence, voxel size: 0.59x0.59x1mm, TR/TE/ΔTE=44/7.2/6.2ms, 5 echoes, bandwidth 550.5 Hz. The unwrapped phase was background filtered with LBV⁵ and VSHARP⁶ . Susceptibility estimation was performed with WH-QSM [ref Milovic MRM 2018b]. We used the estimated harmonic phase to further subtract background remnants prior to our proposed hybrid method. We compared susceptibility estimations from WH-QSM and our hybrid method.

Results

Experiment A: our method does not propagate artefacts due to phase jumps (Fig 1). Experiment B: RMSE-based errors in the defined interval were increased by less than 15% (Fig2). This implies our proposed method is stable for a wide range of regularization weights. Experiment C: good reconstructions were achieved with both our proposed method and WH-QSM (Fig 3). The difference map between these methods reveals that the hybrid method effectively suppressed minor streaking artefacts emanating from the venous system and calcifications.

The L1-norm is more robust against streaking artefacts than the L2-norm, as revealed by the introduced phase jump. Nevertheless, L1-norm still has a small error around the phase jump. The sequential combination of the norms solves that problem. With more iterations, the hybrid method has a more natural appearance than the L1 inversion.We showed that our method also gives good results when working with in vivo data. The hybrid data fidelity combines the best features of both norms. The L1-norm provides robustness to extreme noise and phase inconsistencies, preventing streaking artifacts and its propagation. The L2-norm provides a better regularization, allowing a better reduction of noise in the phase data that is well represented by a Gaussian distribution. This prevents a texturized appearance, often seen in L1-norm solutions.Tienes que ser mas explicito con esto

Acknowledgements

Grant funding Fondecyt 1191710, Anillo 190064, Millenium Science Initiative of the Ministry of Economy, Development and Tourism, grant Nucleus for Cardiovascular Magnetic Resonance.

References

1. Marques et al ISMRM 2019. 2.Milovic et al QSM Workshop Korea 2019. 3. Bilgic SPIE 2015, Milovic MRM 2018. 4. Marques ISMRM 2019. 5. Zhou D et., al 2014. 6. Bilgic B et., al. 2014