Introduction

Accurate, whole head magnetic susceptibility reconstruction from tissue field data is a current challenge in the field of quantitative susceptibility mapping. To avoid background field removal imperfections from negatively impacting the subsequent local field inversion steps and to map susceptibility of the entire tissue region of interest, a number of total field algorithms have been developed, which use preconditioning or regularization. ^1,2,3 This abstract proposes an improvement over a previously proposed regularization approach, LN-QSM. It uses biophysical information such as R2* and spatial frequency information to inform the regularization term. The proposed algorithm, called TFIR (Total Field Inversion Regularized) is compared with that of LN-QSM and traditional local field inversion in phantom data and in patient data, both with and without hemorrhage.

Methods

In TFIR, the below cost function is minimized. $$\chi^{*} = argmin_{\chi} \frac{1}{2} ||w(f-d \ast \chi)||^{2}_{2} + \lambda_{1}||M_{G}\nabla \chi||_{1} + \lambda_{2} ||e^{-|\kappa (k \ast R2^{*})|} (k \ast \chi)||^{2}_{2}$$where $$$\kappa$$$ is a low pass filter (chosen here as the spherical mean value operator (SMV) with radius 5mm),$$$\lambda_{2}$$$ is a scalar and is a regularization parameter. The spatially varying weight is meant to impose an assumed susceptibility histogram. This form for the weight assumes that the estimated susceptibility is roughly proportional to R2* and that its histogram can be empirically approximated by an exponentially decaying function with decay parameter . This parameter can be estimated by an exponential fit to the R2* histogram. In this work, we instead chose optimal values for $$$\lambda_{2}$$$ and $$$\kappa$$$ by minimizing the reconstruction error of a multiple orientation data using the COSMOS⁴ reconstruction as ground truth. This method is compared with a local field inversion method (PDF-MEDI)⁵ with a SMV operation included in the dipole kernel to remove remaining background field and with LN-QSM using the regularization parameter value suggested by the authors.
The optimization of $$$\lambda_{2}$$$ (for LN-QSM and TFI-R) and $$$\kappa$$$ (for TFI-R) was based on minimizing the reconstruction error. Error compared to known values in COSMOS and phantom data is optimized on a two dimensional grid across $$$\lambda_{2}$$$ and $$$\kappa$$$, higher resolution optimization will be performed in future to analyze potential for multiple optimal points. The optimal values found for TFIR and reported in results are the values used for all the reconstructions.
A phantom was constructed by embedding Gadolinium containing wells (concentrations ranging from 0.625 mM to 10 mM) in an agarose phantom. Imaging was performed in a Siemens Prisma 3T in a head coil. Imaging parameters are 0.5625 x 0.5625 x 0.6 mm voxel size with 230x320x96 matrix size.
Multiple orientation gradient echo data was acquired in N=4 healthy subjects using Imaging parameters similar to 0.5 x 0.5 x 1 mm voxel size with 512x512x172 matrix size, number of echos > 6 are used. N=9 patients without and N=10 patients with hemorrhage in which a brain multiple echo gradient echo data was acquired were selected for retrospective analysis. Imaging parameters varied across patients. For all data sets, QSM was computed using each of the 3 methods. In order to compare the three methods, the mask in which the PDF MEDI-SMV reconstruction was performed was selected for error computation. A measure for shadowing artifact was computed by taking the variance of the susceptibility values below 0.1 ppm.

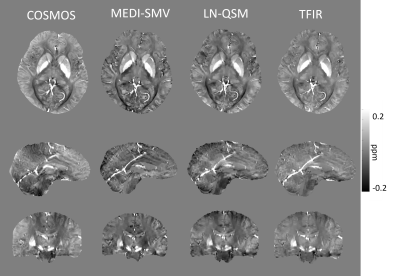
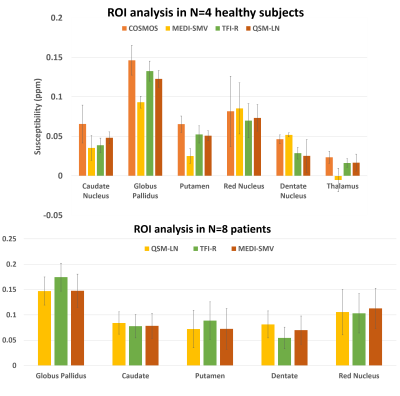
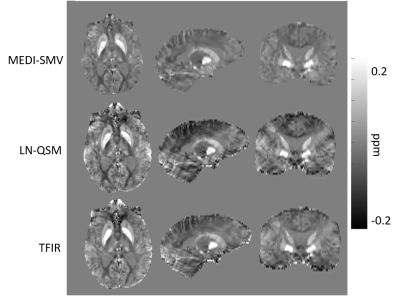
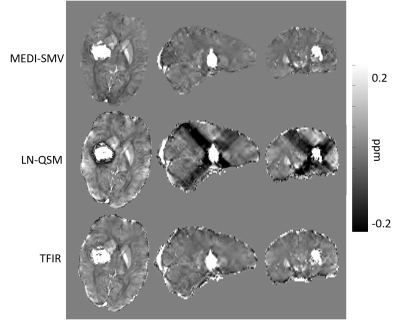
Results

Optimal TFIR parameters for the Gadolinium phantom were $$$\kappa$$$ = 0.1 and $$$\lambda_{2}$$$ = 2.5x10-5. Resultant gadolinium phantom analysis is shown in Figure 1. Based on the COSMOS data, the optimal parameter values for TFIR for in-vivo brain scans are $$$\lambda_{2}$$$= 0.1 and $$$\kappa$$$= 0.1. Results from COSMOS analysis are shown in Figure 2. RMSE with respect to the COSMOS result was 0.0304, 0.0316 and 0.0225 for PDF-MEDI-SMV, LN-QSM, and TFI-R, respectively, with greater accuracy for TFIR compared to LN-QSM and PDF-MEDI-SMV and reduced appearance or artifacts. Figure 3 shows ROI analysis results in the COSMOS data. For deep brain matter, the accuracy of total field methods exceeds background field methods (PDF-MEDI-SMV). MEDI-SMV local field inversion significantly underestimates many ROIs, with TFIR provides accurate results compared to COSMOS and retains dynamic range. Among the patients, N=10 were found to have hemorrhage, and N=9 were analyzed that do not have a hemorrhage pathology. Figure 4 shows an example in a non-hemorrhage patient. Shadow artifact measure was 1.1 ± 0.48, 5.4± 4, and 2.3 ± 1.4 ppb reported for PDF-MEDI-SMV, LN-QSM, and TFIR, respectively. Figure 5 shows an example in a patient with hemorrhage. Shadow artifact measure was 0.28 ± 0.064, 1.8±0.94, and 1.2±0.74 ppb reported for PDF-MEDI, LN-QSM, and TFIR respectively.

Conclusions and Future Directions

TFIR allows the removal of unwanted shadowing artifacts and more accurately maps susceptibility than other regularization total field method such as LN-QSM and local field methods such as PDF-MEDI-SMV. In future, optimal filter kernel selection will be performed and automated for each individual dataset in order to best utilize spatial frequency information.

Acknowledgements

The authors would like to acknowledge all collaborators and funding support for graduate school.