Introduction

Quantitative susceptibility mapping (QSM) is a potential method in MRI for mapping the magnetic microstructure of the brain¹. In current QSM^2-5, the gradient recalled echo (GRE) signal phase is related to a discrete convolution between an apparent bulk magnetic susceptibility tensor (BMST) and the point-dipole kernel. In this study, we show that the contribution from the demagnetization field measured in a voxel, for short echo times, is related instead to the magnetometric demagnetization field. This introduces a new “magnetometric dipole kernel” for QSM. We implemented this new technique and tested it on the 2016 QSM Challenge⁶ phase data, where this lead to sharper looking susceptibility maps.

Methods

Consider a medium with impermeable, MRI-invisible magnetic inclusions with an associated susceptibility tensor $$$\chi_{\alpha\beta}(\vec{r})$$$ relative to the surrounding MRI-visible fluid. The water containing volume is characterized by the indicator function $$$u(\vec{r})$$$ equal to one inside the fluid and zero otherwise. When placed in a static magnetic field $$$(B_0)_\alpha=B_0n_\alpha$$$ along $$$\hat{n}$$$, the inclusions generate a secondary field which induces a shift in the local Larmor frequency in the MRI-visible fluid⁷
$$\Delta\Omega(\vec{r})=u(\vec{r}){\gamma}B_{0}n_{\alpha}\left\{\int_{LC(\vec{r})}d\vec{r}^{\prime} N_{\alpha\beta}^{(P)}\left(\vec{r}-\vec{r}^{\prime}\right)\chi_{\beta\gamma}\left(\vec{r}^{\prime}\right)-{\int}d \vec{r}^{\prime}N_{\alpha\beta}^{(P)}\left(\vec{r}-\vec{r}^{\prime}\right)\chi_{\beta\gamma}\left(\vec{r}^{\prime}\right)\right\}n_{\gamma},$$ where
$$N_{\alpha\beta}^{(P)}(\vec{r})=\frac{3r_{\alpha}r_{\beta}-\delta_{\alpha\beta}}{r^{3}}$$
is the elementary dipole field and $$$"LC(\vec{r})"$$$ denotes the region of the local Lorentz cavity field correction at $$$\vec{r}$$$, where the shape of the cavity accounts for the magnetic microstructure⁸, and a zero average field inside by summation of the explicit dipole fields, from the near environment of $$$\vec{r}$$$.

The normalized GRE signal in the rotating frame from the MRI-visible fluid within a volume $$$V_i$$$ exposed to this field perturbation is given by the ensemble average $$$\langle\cdot\rangle_{\mathrm{spin}}$$$

$$S(t,i)=\left\langle{e^{i\varphi(t,i))}}\right\rangle_{\mathrm{spin}},\quad\varphi(t,i)=\int_{0}^{t}dt^{\prime} \Delta\Omega\left(t^{\prime},i\right),$$
where $$$"i"$$$ denote the center of the voxel $$$V_i$$$, and $$$\Delta \Omega\left(t,i\right)$$$ is the instantaneous Larmor frequency offset felt by a spin along its trajectory within the volume $$$V_i$$$. Assuming that the signal is sampled at a sufficiently short echo time, so the diffusion length is much shorter than the characteristic length scale of the induced field, the signal can be characterized by the first cumulant $$$\left\langle\varphi(t,i)\right\rangle=\left\langle\Omega \right\rangle_it$$$, where $$$\left\langle\cdot\right\rangle_i$$$ denotes a spatial average over $$$V_i$$$. The signal phase then arises as a spatial average over the entire medium, which we sub-divide into voxels of volume $$$V_j$$$

$$\begin{aligned}\langle\Delta\Omega\rangle_{i}={\gamma}B_{0}n_{\alpha}\frac{1}{\zeta_{i}V_{i}} \int_{V_{i}}d\vec{r}^{\prime}u\left(\vec{r}^{\prime}\right)\left\{\int_{LC\left(\vec{r}^{\prime}\right)}d\vec{r}^{\prime\prime}N_{\alpha\beta}^{(P)}\left(\vec{r}^{\prime}-\vec{r}^{\prime\prime}\right)\chi_{\beta\gamma}\left(\vec{r}^{\prime\prime}\right)-\sum_{j}\int_{V_{j}}d\vec{r}^{\prime\prime}N_{\alpha\beta}^{(P)}\left(\vec{r}^{\prime}-\vec{r}^{\prime\prime}\right)\chi_{\beta\gamma}\left(\vec{r}^{\prime\prime}\right)\right\}n_{\gamma}, \end{aligned}$$ where $$$\zeta_i$$$ denotes the MRI-visible volume fraction in $$$V_i$$$. The indicator function, dipole field and magnetic susceptibility can also be expressed by their voxel averages $$\begin{aligned}u\left(\vec{r}^{\prime}\right)=\frac{1}{V_{i}} \int_{V_{i}}d\vec{r}^{\prime\prime}u\left(\vec{r}^{\prime\prime}\right)+\delta{u}\left(\vec{r}^{\prime}\right)=\zeta_{i}+\delta{u}\left(\vec{r}^{\prime}\right),\\
N_{\alpha\beta}^{(P)}\left(\vec{r}^{\prime}-\vec{r}^{\prime\prime}\right)= \frac{1}{V_j}\int_{V_j}d\vec{r}^{\prime\prime\prime}N_{\alpha\beta}^{(P)}\left(\vec{r}^{\prime}-\vec{r}^{\prime\prime\prime}\right)+\delta N_{\alpha \beta}^{(P)}\left(\vec{r}^{\prime}-\vec{r}^{\prime\prime}\right),\\\chi_{\alpha\beta}\left(\vec{r}^{\prime\prime}\right)= \frac{1}{V_j}\int_{V_j}d\vec{r}^{\prime\prime\prime}\chi_{\alpha\beta}\left(\vec{r}^{\prime\prime\prime}\right)+\delta\chi_{\alpha\beta}\left(\vec{r}^{\prime\prime}\right).\end{aligned}$$
Assuming $$$\zeta_i\approx1$$$, a low intra-voxel variation in the susceptibility and demagnetization tensor convolution $$$\sum_{j}\int_{V_{j}}d\vec{r}^{\prime\prime}{\delta}N_{\alpha\beta}^{(P)}\left(\vec{r}^{\prime}-\vec{r}^{\prime\prime}\right)\delta\chi_{\beta\gamma}\left(\vec{r}^{\prime\prime}\right)\approx{0}$$$ and that the average Larmor correction within $$$V_i$$$ corresponds to an isotropic magnetic compartment, we obtain an average Larmor frequency shift
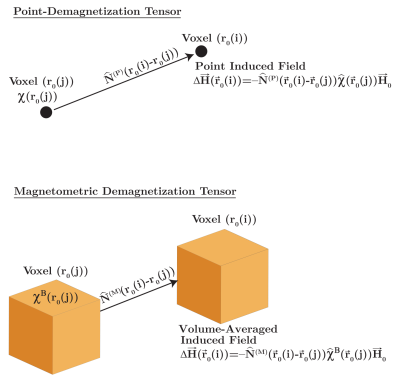
$$\begin{aligned}\langle\Delta\Omega\rangle_{i}&={\gamma}B_{0}n_{\alpha}\left\{\frac{1}{3} \delta_{\alpha\beta}\chi_{\beta\gamma}^{B}(i)-\sum_{j}N_{\alpha\beta}^{(M)}(i-j)\chi_{\beta\gamma}^{B}(j)\right\}n_{\gamma},\\N_{\alpha\beta}^{(M)}(i-j)&\equiv\frac{1}{V_{i}}\int_{V_{i}}d\vec{r}^{\prime}\int_{V_{j}}d\vec{r}^{\prime\prime}N_{\alpha\beta}^{(P)}\left(\vec{r}^{\prime}-\vec{r}^{\prime\prime}\right),\end{aligned}$$ where $$$\chi_{\alpha\beta}^{B}(j)\equiv\frac{1}{V_{j}}\int_{V_{j}}d\vec{r}^{\prime\prime}\chi_{\alpha\beta}\left(\vec{r}^{\prime\prime}\right)$$$ and $$$N_{\alpha\beta}^{(M)}(i-j)$$$ denotes the BMST and magnetometric demagnetization tensor respectively. Figure 1 illustrates the difference between $$$N_{\alpha\beta}^{(M)}$$$ and $$$N_{\alpha\beta}^{(P)}$$$. In Fourier space we obtain
$$\begin{aligned}\langle\Delta \Omega\rangle_{i}(\vec{k})&={\gamma}B_{0}n_{\alpha}K_{\alpha\beta}^{(M)}(\vec{k})\chi_{\beta\gamma}^{B}(\vec{k})n_{\gamma},\\K_{\alpha\beta}^{(M)}(\vec{k})&\equiv\frac{1}{3}\delta_{\alpha\beta}-N_{\alpha\beta}^{(M)}(\vec{k}),\end{aligned}$$ where $$$K_{\alpha\beta}^{(M)}(\vec{k})$$$ defines the magnetometric dipole kernel, which yields a different demagnetization field compared to the point-dipole kernel^9,10 $$K_{\alpha\beta}^{(P)}(\vec{k})=\frac{1}{3}\delta_{\alpha\beta}-N_{\alpha\beta}^{(P)}(\vec{k})=\frac{1}{3}\delta_{\alpha\beta}-\frac{k_{\alpha}k_{\beta}}{k^{2}}.$$ For rectangular voxels with dimensions $$$\left(d_{x},d_{y},d_{z}\right),$$$ $$$N_{\alpha\beta}^{(M)}\left(i-j)\right)=N_{\alpha\beta}^{(M)}(x,y,z)$$$ can be calculated analytically^11,12
$$N_{\alpha\beta}^{(M)}(x,y,z)=\frac{1}{4{\pi}d_{x}d_{y} d_{z}}\sum_{\epsilon_{1},\epsilon_{2},\epsilon_{3}=-1}^{1}\frac{8}{(-2)^{\left(\left|\epsilon_{1}\right|+\left|\epsilon_{2}\right|+\left|\epsilon_{3}\right|\right)}}\Phi_{\alpha\beta}\left(x+\epsilon_{1}d_{x},y+\epsilon_{2}d_{y},z+\epsilon_{3}d_{z}\right),$$ with auxiliary functions
$$\begin{aligned}\Phi_{xx}=&\frac{1}{6}\left(2x^{2}-y^{2}-z^{2}\right)R+\frac{1}{2}y\left(z^{2}-x^{2}\right)\log(y+R)+\frac{1}{2}z\left(y^{2}-x^{2}\right)\log(z+R)-xyz\operatorname{atan}\left(\frac{yz}{xR}\right),\\\Phi_{xy}=&-\frac{1}{3}xyz+xyz\log(z+R)+\frac{1}{6}y\left(3z^{2}-y^{2}\right)\log(x+R)+\frac{1}{6}x\left(3z^{2}-x^{2}\right)\log(y+R)\\&-\frac{1}{6}z^{3}\operatorname{atan}\left(\frac{xy}{zR}\right)-\frac{1}{2}y^{2}z\operatorname{atan}\left(\frac{xz}{yR}\right)-\frac{1}{6}x^{2}\operatorname{atan}\left(\frac{yz}{xR}\right),\\R=&\sqrt{x^{2}+y^{2}+z^{2}}.\end{aligned}$$ The remaining components are given by cyclic permutation and the symmetry of the auxiliary functions.

Application:
As the average frequency shift has the same functional form as in previous QSM methods, it is straightforward to adapt an LSQR algorithm for “Magnetometric” STI (MSTI). Based on phase data openly available from the 2016 QSM challenge⁶ we estimate the apparent BMST based on regular STI and MSTI.

Results

Figure 2 shows $$$\chi_{zz}^{(MSTI)}$$$, $$$\chi_{zz}^{(STI)}$$$, and $$$\Delta\chi_{zz}=\chi_{zz}^{(MSTI)}-\chi_{zz}^{(STI)}$$$ from the 2016 QSM challenge phase data based on both STI and MSTI LSQR algorithms.

Discussion

Figure 2 demonstrates an obvious improvement in the sharpness of MSTI compared to STI, with much more detail visible in MSTI. The reason for this effect, when performing STI, stems from not performing the spatial averaging over $$$V_i$$$ and $$$V_j$$$ in STI. To estimate the relationship between the susceptibility derived from $$$K_{\alpha\beta}^{(M)}$$$ and $$$K_{\alpha\beta}^{(P)},$$$ we define a BMST $$$\tilde{\chi}_{\alpha\beta}^{B}(j)$$$ by forcing the equality
$$\langle\Delta\Omega\rangle_{i}={\gamma}B_{0}n_{\alpha}\left[\frac{1}{3}\delta_{\alpha\beta}\tilde{\chi}_{\beta\gamma}^{B}(i)-\sum_{j}N_{\alpha\beta}^{(P)}(i-j)\tilde{\chi}_{\beta\gamma}^{B}(j)\right] n_{\gamma},$$
which leads to a LSQR expression
$$\tilde{\chi}_{\beta\gamma}^{B}(\vec{k})=\left(K_{\beta\rho}^{(P)}(\vec{k})K_{\rho\mu}^{(P)}(\vec{k})\right)^{-1}K_{\mu\epsilon}^{(P)}(\vec{k})K_{\epsilon\alpha}^{(M)}(k)\chi_{\alpha\gamma}^{B}(\vec{k})\equiv{T_{\beta\alpha}}\left[\chi_{\alpha\gamma}^{B}(\vec{k})\right],$$

where $$$T_{\beta\alpha}$$$ defines a linear transformation between the susceptibilities. This is visualized in figure 3 by applying $$$T_{\beta\alpha}$$$ on $$$\chi_{zz}^{(STI)}$$$ and $$$\chi_{zz}^{(MSTI)}$$$.

Limitations:
$$$K_{\alpha\beta}^{(M)}$$$ shares other model assumptions with $$$K_{\alpha\beta}^{(P)}$$$, such as a high water fraction, a low intra-voxel variation in both susceptibility and demagnetization tensor components, and an average spherical Lorentz cavity. These assumptions are violated in many areas of the brain¹³, such as in white matter, and must be properly accounted for. Calculating the components of $$$N_{\alpha\beta}^{(M)}$$$ must also be done with high numerical precision as they are prone to catastrophic cancellation.

Conclusion

By examining the voxel signal for short echo times from an MRI-visible fluid surrounded by MRI-invisible magnetic inclusions, we find that the voxel-averaged Larmor frequency shift is related to the magnetometric demagnetization field. This defines a new “magnetometric dipole kernel”. Using the phase data from the 2016 QSM Challenge, we find that the magnetometric dipole kernel increases the sharpness of the apparent BMST maps. In the future, more work will be put in to relaxing the model assumptions further, evaluating the accuracy and regime of validity, and hopefully, getting QSM one step closer to becoming a useful tool in mapping important biomarkers of neurodegenerative diseases.

Acknowledgements

This study is funded by the Independent Research Fund (grant 8020-00158B), Denmark. The authors would like to thank PhD student Jonas Lynge Olesen for many fruitful discussions.