Introduction

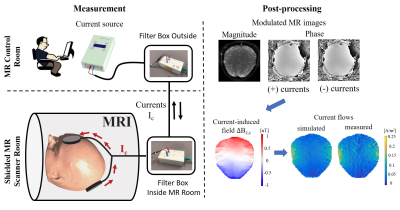
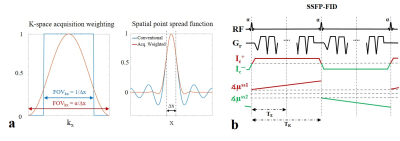
Exact knowledge of the spatial distribution of currents flowing inside the human brain is important for several neuroscientific applications, e.g. for improving non-invasive brain stimulation techniques used for the treatment of neuropsychiatric diseases. MR current density imaging (MRCDI) is a non-invasive method that combines externally injected weak currents with MR to estimate the current flows in the brain based on induced magnetic field measurements (1). The component ∆Bz,c of the current-induced magnetic field parallel to the scanner field, modulates the phase of the MR signal. The signal phase can thus be used for ∆Bz,c calculations and current flow reconstructions (Fig. 1) (2). Accurate current flow reconstructions require highly sensitive ∆Bz,c measurements with a good spatial resolution. Recently, we have reported reliable MRCDI measurements in the human brain with a sensitivity of ~0.1 nT (2). This unprecedented sensitivity is promising, but nevertheless insufficient. As the employed current flow reconstruction algorithm (3) uses the directional derivative of ∆Bz,c, poor spatial resolution and physiological noise and/or very sharp local conductivity changes can cause artifacts. Unfiltered conventional MR imaging, where the k-space sampling density is constant within a rectangular window, has a sinc-shaped spatial point spread function (PSF; Fig. 2a). This causes Gibbs ringing near high-contrast boundaries. The spatial resolution can be improved without signal-to-noise-ratio (SNR) loss by matching the sampling density to a filter that suppresses ringing that is particularly problematic when spatial derivatives are needed (Fig. 2a; acquisition-weighting AW) (4). Here, we explore how AW-MRCDI can improve the sensitivity and spatial resolution of current-induced field measurements and thus current-flow reconstructions by phantom experiments.

Methods

We simulated the spatial point spread functions (PSFs) for a conventional and a weighted acquisition scheme (Fig 2a.). The PSFs were calculated for a nominal voxel size ∆x = 2 mm. In the AW scheme, we used a Hanning window $$$h(k_x)=\frac{1}{2}(1+cos(\frac{2πkx∆x}{α}))$$$ with α=1.61 as suggested in (5). We also performed MRCDI measurements based on steady-state free precession free induction decay (SSFP-FID; Fig. 2b) with multiple gradient-echo readouts in a spherical phantom filled with a saline solution (0.1mM MnCl2+1.5g/L NaCl). An insulating cylindrical tube was inserted inside the sphere and filled with a gel (0.1mM MnCl2+1.5g/L NaCl+1g/L TX151). Two copper tape electrodes were inserted into the two tips of the cylindrical tube for current injection. The experiments were performed at 3T (MAGNETOM Prisma, SIEMENS Healthcare, Erlangen, Germany) with image matrix 112x90, voxel size 2x2x5 mm³, tip-angle α=30˚, repetition time TR=80 ms, number of sampled gradient-echos N_GE=8, echo times TE=[6, 15.6, 25.2, 34.8, 44.4, 54, 63.6, 73.3] ms. First, we injected alternating currents of I_c=+/-1 mA constrained in the cylindrical tube. The current waveform was synchronized with the MR sequence (Fig 2b). The current-induced fields ∆Bz,c were calculated from measured MR phase images. The echoes were combined systematically to optimize the method’s sensitivity to ∆Bz,c as in (2,6). The norm of the gradient of the current-induced field ∇(∆Bz,c) images were compared (the relevant component of the current-density estimate):
Experiment 1: The signal at each k-space point was acquired N_meas=18 times to increase the SNR. The total scan time was T_tot = 4 mins 20 sec (uniform k-space weighting).
Experiment 2: N_meas was systematically changed for each k-space point (more averages in the center than the outer regions, Fig. 2) with T_tot = 3 mins 38 sec. The acquired signal was then weighted with a matched Hanning filter (Fig 2a.).
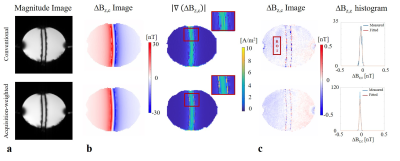
Second, the experiments were repeated without current injection I_c = 0 mA to compare sensitivity of the two cases. The noise floors were calculated in a selected region-of-interest (ROI) in the ∆Bz,c images (Fig 3.; measurements were fitted to a Gaussian distribution and its standard deviation σ_∆Bz,c was calculated).

Results and Discussion

The simulated PSFs (Fig 2a.) demonstrate that the side lobes causing ringing in the MR images can be significantly suppressed by means of a weighted acquisition scheme. This is confirmed by measurement (Fig 3.): The ringing observed in conventional MR magnitude and ∆Bz,c images are corrected in the acquisition-weighted images. The method’s efficiency is more clearly observed in the norm of the current-induced field gradient ∇∆Bz,c (no artefactual fluctuations inside the tube were observed for AW-MRCDI). Also, the noise floor comparisons in the control measurements without currents demonstrate that AW-MRCDI can improve sensitivity 59% for an identical total scan time (σ_∆Bz,c= 22.4 pT for conventional and 15.4 pT for weighted acquisition schemes). The observed ringing is stronger in this phantom experiment compared to our recent MRCDI study (2) in human brain. Therefore, we expect a less visible improvement in-vivo. The spatial resolution of MRI acquired conventionally can always be improved by post-filtering, but with an SNR compromise compared to matched acquisition-weighting.

Conclusion

AW-MRCDI demonstrated a significant improvement in sensitivity and spatial resolution, which is essential for MRCDI relying on calculation of spatial derivatives. The performance in-vivo remains to be explored.

Acknowledgements

The project is supported by Lundbeck foundation with grant number R288-2018-236.