3172
Investigation on the estimation performance of phase-based T2 mapping in the presence of motion
Daiki Tamada1, Xiaoke Wang1, Timothy J. Colgan1, Diego Hernando1,2, and Scott B. Reeder1,2,3,4,5
1Radiology, University of Wisconsin-Madison, Madison, WI, United States, 2Medical Physics, University of Wisconsin-Madison, Madison, WI, United States, 3Biomedical Engineering, University of Wisconsin-Madison, Madison, WI, United States, 4Medicine, University of Wisconsin-Madison, Madison, WI, United States, 5Emergency Medicine, University of Wisconsin-Madison, Madison, WI, United States
1Radiology, University of Wisconsin-Madison, Madison, WI, United States, 2Medical Physics, University of Wisconsin-Madison, Madison, WI, United States, 3Biomedical Engineering, University of Wisconsin-Madison, Madison, WI, United States, 4Medicine, University of Wisconsin-Madison, Madison, WI, United States, 5Emergency Medicine, University of Wisconsin-Madison, Madison, WI, United States
Synopsis
The estimation performance of phase-based T2 mapping in the presence of motion was investigated using Bloch equation simulations. The steady-state signal of RF-phase modulated gradient echo imaging in the presence of motion was calculated. Linear, sinusoidal, and random motion were considered for the simulation. The results showed that phase errors induced by motion may lead to underestimation of T2 when using a gradient echo phase-based T2 mapping method.
Introduction
Recently, a phase-based T2 mapping method, that encodes T2 information into the phase of the steady-state signal of RF-phase modulated gradient echo (GRE) imaging, has been proposed1. This novel method enables high resolution and three-dimensional imaging. However, it has also been demonstrated that this phase-based T2 mapping method may be confounded by motion2.Phase errors due to the effects of motion may lead to non-negligible changes in the steady-state GRE signal. RF phase modulation in the form of a quadratically increasing phase is widely used for the T1-weighted spoiled gradient echo (SGRE) imaging3,4. In the body imaging using SGRE sequences, physiological motion can affect the steady-state of the signal5,6. Motion during TR can lead to phase shifts since spins experience a different magnetic field generated by an unbalanced gradient waveform. This phase shift may impact the steady-state signal phase, and lead to incorrect estimation of T2.
In this study, the steady-state GRE signal in the presence of motion was investigated using Bloch equation simulations. The results indicated that the motion caused a non-negligible underestimation of T2.
Methods
T2 was estimated using two GRE imaging acquisitions with different transmit RF-phase incremented quadratically ($$$\Delta \phi$$$)2. The relationship between $$$\Delta \phi$$$ and the phase of the steady-state signal of GRE for a specific T1 and T2 can be expressed by the following equation1.$$\theta(\Delta \phi, \alpha, TR;T1,T2)=\angle S_1 (\Delta \phi, \alpha, TR;T1,T2) - \angle S_2 (-\Delta \phi, \alpha, TR;T1,T2)$$
where α is a flip angle. Since the phase becomes less sensitive to T1 with relatively long T1 (> 1000 ms)1, θ largely depends only on T2. The phase based T2 mapping method estimates T2 using a lookup table calculated using Bloch equation simulations7.
To evaluate the signal evolution of the GRE sequence in the presence of motion, Bloch equation simulations were performed. The GRE sequence consists of an RF pulse, rewinder, and readout (RO) gradient, as shown in Fig. 1. The phase shift $$$\phi_m$$$ due to motion in the presence of a constant gradient can be formulated as below.
$$\phi_m = \int_{0}^{\tau} G \cdot r(t) dt$$
where G is a magnetic field generated by the gradient coil, r is the position of a spin along the RO direction, and τ is a time duration spin experience the field. This equation can be approximated using Taylor expansion as below.
$$\phi_m \sim G(\nu \cdot TR \cdot n + r_0) \cdot \tau + \frac{G}{2} \nu \cdot \tau^2$$
where $$$\nu$$$ is a velocity of the motion. Sequence parameters for the Bloch equation simulation were as follows: TR = 10 ms, FOV = 40 cm, flip angle = 20°, number of sampling points = 256, receiver bandwidth = 195 Hz/px.
We calculated the signal evolution in the presence of three different types of motion:
- Linear motion: with constant velocity of 0.1 mm/s along the RO direction
- Sinusoidal motion: with frequency 0.25 Hz and amplitude 0.2mm
- Random motion: random velocity with a Gaussian distribution (mean = 0 mm/s, and standard deviation = 0.2 mm/s )
Results
The signal evolutions with the linear, sinusoidal, and random motions are shown in Fig. 2 (a-c). Difference of mean signal magnitude between with and without motion was less than 0.5 %. Coefficient of variations of signal magnitude in the last 200 TRs for the linear, sinusoidal, and random motions were 0.0, 0.44, and 0.64 %, respectively. The mean difference of phases between with and without motion for those motions were 0.61, 0.055, and 0.0081°, respectively.The phase and T2 estimation error caused by the linear motion are shown in Fig. 3(a-c). The results implied the motion induced phase error caused underestimation of T2. In case of the velocity of ±3.0 mm/s and T2 of 200 ms, estimated T2 values using $$$\Delta \phi$$$ of 2°, 4°, and 6° were decreased by 98.5, 74.0, and 25 %, respectively.
Discussion
In this work, we have shown through Bloch equation simulation that motion impacts estimation of a phase-based T2 mapping method. The specific impact depends on the motion, T1, T2, and $$$\Delta \phi$$$. These simulations demonstrate that linear motion biases the magnitude and the phase of the steady-state signal, leading to potential underestimation of T2.Further, these results suggest two primary strategies to reduce the effects of the motion. Balancing the gradient moment is a straightforward solution, ie: balanced steady-state free precession (bSSFP), although this leads to sensitivity to the off-resonance. An alternative strategy is to use a larger RF phase increment, $$$\Delta \phi$$$. However, the phase of the signal becomes less sensitive to T2 because the use of very large $$$\Delta \phi$$$ can lead to elimination of coherent transverse magnetization.
Conclusion
Phase errors induced by motion may lead to underestimation of T2, when using a gradient echo phase-based T2 mapping method.Acknowledgements
We wish to acknowledge support from the NIH (R01 DK083380, R01 DK088925, K24 DK102595) and from the University of Wisconsin SEED grant program. Further, we wish to acknowledge GE Healthcare and Bracco Diagnostics who provides research support to the University of Wisconsin. Finally, Dr. Reeder is a Romnes Faculty Fellow, and has received an award provided by the University of Wisconsin-Madison Office of the Vice Chancellor for Research and Graduate Education with funding from the Wisconsin Alumni Research Foundation.References
- Wang, X., Hernando, D., Reeder, S. “A Novel Phase Based T2 Mapping Technique Using Gradient Echo Imaging” ISMRM (2019): 0942[6] Wang, Xiaoke., et al. “Phase-based T2 Mapping with Gradient Echo Imaging”, submitted to Magnetic Resonance in Medicine (2019)
- Wang, Xiaoke., et al. “Phase-based T2 Mapping with Gradient Echo Imaging”, submitted to Magnetic Resonance in Medicine (2019)
- Zur, Y., M. L. Wood, and L. J. Neuringer. "Spoiling of transverse magnetization in steady‐state sequences." Magnetic resonance in medicine 21.2 (1991): 251-263.
- Sobol, Wlad T., and David M. Gauntt. "On the stationary states in gradient echo imaging." Journal of Magnetic Resonance Imaging 6.2 (1996): 384-398.
- Henkelman, R. M., McVeigh, E. R., Crawley, A. P., & Kucharczyk, W. (1989). Very slow in-plane flow with gradient echo imaging. Magnetic resonance imaging, 7(4), 383-393.
- Reeder, S., McVeigh, E., “Velocity spoiling of transverse magnetization: implications for CINE MRI”. SMRM (1993)
- Weigel, M. (2015). Extended phase graphs: dephasing, RF pulses, and echoes‐pure and simple. Journal of Magnetic Resonance Imaging, 41(2), 266-295.
Figures
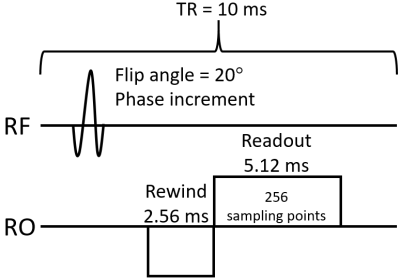
Fig. 1 Pulse sequence consists of a RF, rewinder,
and readout gradient pulses, used for the simulation. Slice-select and
phase-encoding gradient pulse were not assumed.
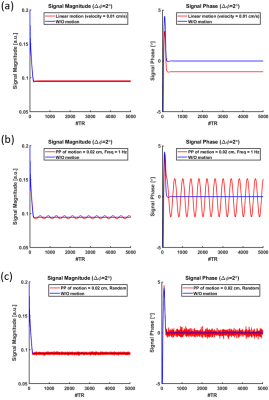
Fig. 2 Signal evolution with (a) linear, (b) sinusoidal, and (c) random motion calculated using Bloch simulation. The linear motion gave a non-negligible phase bias, while the sinusoidal and random motion caused oscillating and random errors in both magnitude and phase of the signal.
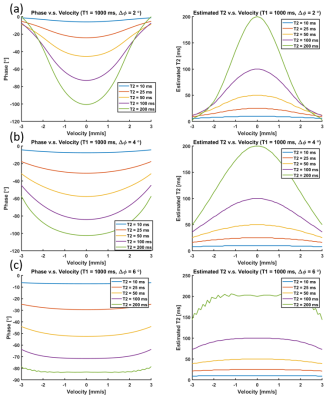
Fig. 3 Phase change
and T2 estimation error induced by linear motion with $$$\Delta \phi$$$ of (a) 2°, (b) 4°, and (c) 6°.
Phase of signal became less sensitive to the motion as larger Df
was used.