3157
A novel T2 relaxation analysis method SAME-ECOS: Spectrum Analysis for Multiple Exponentials via Experimental Condition Oriented Simulation1Physics & Astronomy, University of British Columbia, Vancouver, BC, Canada, 2International Collaboration on Repair Discoveries, Vancouver, BC, Canada, 3Radiology, University of British Columbia, Vancouver, BC, Canada, 4Biomedical Engineering, University of British Columbia, Vancouver, BC, Canada, 5Kinesiology, University of British Columbia, Vancouver, BC, Canada, 6Pathology & Laboratory Medicine, University of British Columbia, Vancouver, BC, Canada
Synopsis
We propose a novel T2 relaxation data analysis method called spectrum analysis for multiple exponentials via experimental condition oriented simulation (SAME-ECOS), which was developed based on a combination of information theory and deep learning neural network algorithms. SAME-ECOS is tailored for different MR experimental conditions to decompose the multi-exponential decay data into a T2 spectrum, which has been considered an ill-posed problem using conventional fitting algorithms including the commonly used non-negative least squares (NNLS). Our results demonstrated that, compared with NNLS, SAME-ECOS can yield much more reliable T2 spectra in a dramatically shorter time.
Introduction
T2 relaxation in biological tissues measured in a multi-echo experiment is typically characterized by multi-exponential decays because multiple water pools exist within each image voxel.1 For example, myelin water, the water trapped by myelin bilayers in white matter (WM), exhibits shorter T2 than intra/extra-cellular water.2 Accurately depicting the T2 spectrum of each voxel from noisy experimental data is nontrivial as decomposition of a multi-exponential decay is an ill-posed problem.3 According to information theory, the decay components can only be resolved to a certain resolution limit at a given signal to noise ratio (SNR).4 Many algorithms, including the commonly used non-negative least squares (NNLS)5, have the theoretical ability to produce the T2 spectrum via fitting the noisy data but often yield unreliable results in practice, especially for in-vivo imaging when SNR is low. Based on our previous work6 of using a deep learning neural network (NN) for double-exponential fitting, we propose a novel spectrum analysis for multiple exponentials via experimental condition oriented simulation (SAME-ECOS), which harnesses the power of information theory and deep learning simultaneously, and has the flexibility of tailoring itself to different experimental conditions. Here we introduce SAME-ECOS by presenting an example workflow.Method
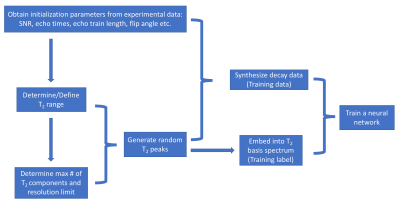
In-vivo MRI experiment: 32-echo data (gradient and spin echo7, TE/ΔTE/TR=10/10/1000ms, refocusing flip angle (FA)=180°, slices=40, resolution=1×1×5mm3) from one healthy volunteer was collected at 3T using an 8-channel SENSE head coil (Philips Achieva).SAME-ECOS workflow (Figure 1). To initialize the analysis, in-vivo experimental SNR in the white matter (segmentation via FSL FAST8) was first determined to be approximately 167 by estimating the noise variance in the 1st echo image. The SAME-ECOS workflow for this particular example is described as follows.
1.Define the T2 range to be 4-1000ms. The optimal lower and upper boundaries can be obtained using equations (1) and (2).3
$$(1):\;T_2^{min} = - \frac{2^{nd}\,echo\,time}{\ln{\frac{1}{SNR}}}$$
$$(2):\;T_2^{max} = - \frac{last\,echo\,time}{\ln{\frac{1}{SNR}}}$$
The 2nd echo is used in (1) because the 1st echo is used later as a normalization factor. The upper boundary is replaced by the default of 1000ms because, based on literatures of brain T2 ranges1,2,7 , the calculated optimal value (63ms) is too short for in-vivo brain imaging analysis.
2. Determine the maximum number of resolvable T2 components to be M=5 by numerically solving equation (3) to the nearest integer for a given SNR and T2 range.9
$$(3):\;\frac{M}{\ln{\frac{T_2^{max}}{T_2^{min}}}}\times\sinh{\left(\frac{\pi^2\times{M}}{\ln{\frac{T_2^{max}}{T_2^{min}}}}\right)} = \left(\frac{SNR}{M}\right)^2$$
Then, the T2 resolution limit δ=3.017 was determined by equation (4).3
$$(4):\;\delta=\left(\frac{T_2^{max}}{T_2^{min}}\right)^{\frac{1}{M}}$$
3. For each simulation realization:
a. generate random integer n≤M and FA∈[90, 180]. Note that the actual FA can deviate substantially from the prescribed FA due to B1 inhomogeneity.
b. generate n randomly located T2 peaks within the T2 range obeying the resolution limit δ.The peak amplitudes were also randomly assigned and normalized to one.
c. synthesize 32-echo decay data using extended phase graph (EPG) algorithm10 by equation (5).
$$(5):\;{decay\,data}=\sum_{i=1}^{i=n}{Amplitude_i\times{EPG(T_{2,i},FA)}}\,+\,{Rician\,distributed\,noise\,(SNR)}$$
Then, the decay data were normalized to the 1st echo and saved for model training.
d. Embed n T2 peaks into a spectrum representation depicted by 40 basis T2s. The 40 basis T2s were equally spaced within the T2 range on a logarithmic scale. Each T2 peak was represented by two nearest basis T2s with weighted amplitudes that were associated with the distances between actual T2 peak and two nearest basis T2s. The embedded T2 basis representation was recorded as the ground truth spectra for model training.
4. Construct a neural network model (hidden layers: 100×500×1000×2000×3000×4000, activation: ReLU11(hidden layers) and softmax12(output layer), optimizer: Adam13, loss: categorical cross-entropy14) to learn the mapping between the simulated decay data and ground truth spectrum (800,000 total realizations for training and validation).
5. Apply the trained SAME-ECOS model to the experimental data (1st echo normalized).
Model evaluation: The SAME-ECOS model was evaluated in two tests and compared with regularized NNLS.
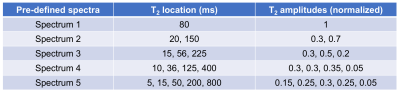
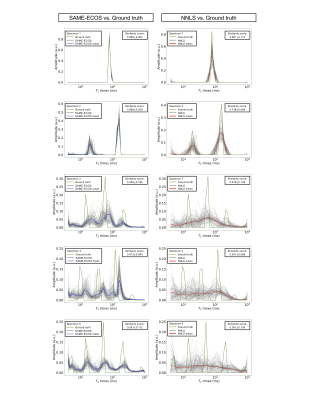
Test 1: Simulated decay data of 5 pre-defined T2 spectra (Table 1), each with 100 different Rician distributed noise realizations, were passed to the trained SAME-ECOS model and regularized NNLS for spectrum predictions. Similarity between each predicted and ground truth spectrum was evaluated by cosine similarity scores.15
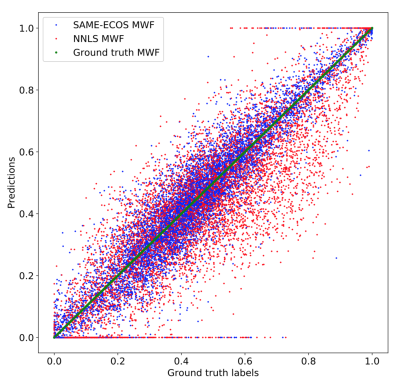
Test 2: 10,000 randomly simulated decay data examples were analyzed by SAME-ECOS and NNLS. The myelin water fraction (MWF, fraction of signal with T2s<40ms) was extracted from each predicted spectrum. Mean absolute error (MAE) in the MWF estimation was computed.
Results and Discussion
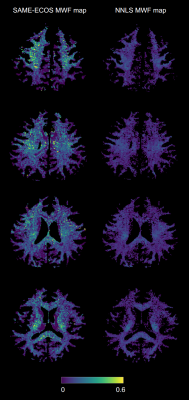
From visual inspection and similarity scores, SAME-ECOS outperformed NNLS in all five scenarios in Test 1 (Figure 2). Both methods were able to produce accurate T2 spectra when the number of T2 components n≤2. However, when n>2, NNLS predictions became extremely unstable (gray lines) and only SAME-ECOS could yield meaningful spectra. For Test 2 (Figure 3), SAME-ECOS MWF (MAE=0.046) demonstrated better agreement with the ground truth than NNLS MWF (MAE=0.081). Finally, WM MWF maps computed from in-vivo data using both methods (Figure 4) showed that SAME-ECOS produced higher mean MWF (0.124) than NNLS (0.075), with a much shorter processing time (7mins vs. 88mins).Conclusion
Our results demonstrated that, compared with NNLS, SAME-ECOS can yield much more reliable T2 spectra in a dramatically shorter time. SAME-ECOS largely surpasses NNLS for multi-echo T2 analysis.Acknowledgements
We thank the study participants and the excellent MRI technologists at the UBC MRI Research Centre. Funding support was provided by the Multiple Sclerosis Society of Canada, Natural Sciences and Engineering Research Council Discovery Grant.References
1. Whittall KP, MacKay AL. Quantitative interpretation of NMR relaxation data. Journal of Magnetic Resonance (1969). 1989;84(1):134-152.
2. MacKay A, Whittall K, Adler J, Li D, Paty D, Graeb D. In vivo visualization of myelin water in brain by magnetic resonance. Magn Reson Med. 1994;31(6):673-677.
3. Istratov AA, Vyvenko OF. Exponential analysis in physical phenomena. Rev Sci Instrum. 1999;70(2):1233-1257.
4. Bertero M, Boccacci P, Pike ER. On the recovery and resolution of exponential relaxation rates from experimental data: A singular-value analysis of the laplace transform inversion in the presence of noise. Proceedings of the Royal Society of London.Series A, Mathematical and Physical Sciences. 1982;383(1784):15-29.
5. Lawson CL, Hanson RJ,1938-, Society for Industrial, Applied Mathematics. Solving least squares problems. [Rev. ed.] ed. Philadelphia : SIAM; 1995.
6. Liu H, Tam r, Kramer J, Laule C. Analyzing multi-exponential T2 decay data using a neural network. Proc. Intl. Soc. Mag. Reson. Med. 2019;27:4886.
7. Prasloski T, Rauscher A, MacKay AL, et al. Rapid whole cerebrum myelin water imaging using a 3D GRASE sequence. Neuroimage. 2012;63(1):533-539.
8. Zhang Y, Brady M, Smith S. Segmentation of brain MR images through a hidden markov random field model and the expectation-maximization algorithm. IEEE Trans Med Imaging. 2001;20(1):45-57.
9. Link N, Bauer S, Ploss B. Analysis of signals from superposed relaxation processes. J Appl Phys. 1991;69(5):2759-2767.
10. Hennig J. Multiecho imaging sequences with low refocusing flip angles. Journal of Magnetic Resonance. 1988;78(3):397-407.
11. Nair V, Hinton GE. Rectified linear units improve restricted boltzmann machines. . 2010:807-814.
12. Bishop CM. Pattern recognition and machine learning. New York: Springer; 2006.
13. Kingma DP, Ba J. Adam: A method for stochastic optimizaton. arXiv. 2014;1412.6980.
14. LeCun Y, Bengio Y, Hinton G. Deep learning. Nature. 2015;521(7553):436-444.
15. Tan PN, Steinbach M, Karpatne A, Kumar V, Introduction to Data Mining, Addison-Wesley (2005), chapter 8, page 500.
Figures