3152

Adaptive and slice-specific z-shimming approach for signal rephasing in 2D multi gradient echo imaging
Martin Soellradl1, Johannes Strasser1, Stefan Ropele1, and Christian Langkammer1
1Department of Neurology, Medical University of Graz, Graz, Austria

Synopsis

Intravoxel dephasing due to macroscopic field variations along the slice-selective direction z can be compensated by application of compensation gradients in z-direction (“z-shimming”). Compensation gradients applied between echo acquisition allow to estimate R2* also in areas with strong field gradients. However, if equally strong compensation gradients are applied in each slice the signal dephases in homogenous areas. We therefore propose an adaptive method where slice-specific compensation gradients are estimated for each slice from a fast pre-scan. With the proposed approach improved R2*-maps, compared to constant compensation gradient strategies, with higher SNR and accuracy can be achieved.

Introduction

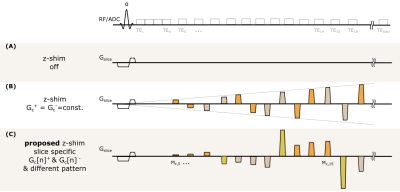
In the presence of macroscopic field variations, the signal of a gradient echo is largely influenced by intravoxel dephasing. Consequently, the faster signal decay hampers quantification of tissue specific parameters such as R2*. Even post-processing approaches1-3 cannot yield reliable parameter estimation in areas with a strong macroscopic field gradient Gz. As a more advanced approach, z-shimming techniques have been proposed which apply a compensation gradient Gc to partly rephase the effect of Gz4–6. By applying a constant positive and negative Gc+/- between the acquisition of subsequent echoes, improved R2*-mapping is possible7 (Figure 1B). However, this method applies the same Gc+/- for each slice and thus signal in homogenous areas with low Gz is crushed.
Here, we propose an adaptive approach where slice-specific compensation gradients Gc[n]+/- are applied for the nth slice. In addition, instead of a single constantGc[n]+/- value we apply different ratios of Gc[n]+/- (Figure 1C) to increase signal rephasing capacity. We demonstrate in phantom and in-vivo measurements that R2*-maps can be significantly improved regarding accuracy and SNR when compared to approaches with post-processing and z-shimming with constant Gc+/-.

Methods

The proposed pattern of compensation gradients for the adaptive z-shimming is illustrated in Figure 1C. There are two major differences to the z-shimming method with constant Gc+/- (Figure 1B): First, slice specific compensation gradients Gc[n]+/- are estimated from a field gradient map (Gz-map) obtained from the field map of a fast pre-scan and the compensation moments are then calculated for the ith echo at echo time TEi within the sequence. Second, Gc[n]+/- is split into three parts [1/3, 2/3, 3/3]Gc[n]+/- to increase the coverage of compensation gradients. After a series of three compensation gradients the applied moment is entirely rephased to obtain an echo with zero z-shim moment.
Signal modelling & implementation: For a train of compensation gradient $$$ \bar G_{c,i}[n]$$$ applied with duration tc, the total moment M[n]c,i after the ith echo is given by:
$$M[n]_{c,i} = \sum_{i=1}^{TE_i} \bar G_{c,i}[n] t_c = G_{c,i}[n]TE_i $$
When considering dephasing in presence of Gz, the signal S(TEi) for a 2D spoiled gradient echo with compensation gradients can be modeled as7:
$$S(TE_i)=S_0 \exp(-R_2^*~TE_i) \int_{-\infty}^{\infty} \underline{M}_{xy}(z)\exp(i\gamma(G_z + G_{c,i})z~TE_i )dz$$
where $$$\underline{M}_{xy}(z) $$$ is the complex transverse magnetization, and S0 the signal at TE=0. Equation (2) was solved numerically10.
Phantom Measurements: The proposed method was compared for R2* estimation with the constant z-shim (|Gc+/-=100µT/m|) approach and with post-processing only (Figure 1) in a homogenous phantom. The cylindric phantom (Ø=12cm, length=20cm) consisted of agarose gel (5g/l) doped with Magnevist® (110µmol/l). Besides z-shim gradients, sequence parameter were identical (α=60°;21 echoes;TE1=2.8ms; duration of z-shim gradient tc=2ms;TEnavi=103.4ms; monopolar readout with bandwidth BW=500Hz/Px;TR=3s;resolution=1x1x4mm3;26 slices). The z-shim values were estimated from pre-scan images (resolution=2x2x4mm3;3 echoes;TE1=2.7ms;TE3=6.9ms;PAT2). The raw data was corrected with the navigator echo and combined as described in8,9. Afterwards, R2* maps were estimated by fitting the measured data to Equation (2).
In-vivo Measurements: The proposed method was compared with the constant z-shim (|Gc+/-|=230µT/m) and the post-processing only approach. Two subjects (age=29/32yrs) were measured with a multi gradient echo (mGRE) sequence (α=60°;17 echoes;TE1=3ms;tc=2ms;TEnavi=64.82ms; bipolar readout with BW=500Hz/Px;TR=2.5s;resolution=1.7x1.7x3mm3;35 slices; pre-scan: resolution=2x2x3mm³, TE1=2.7ms;TE3=6.9ms;PAT2).

Results

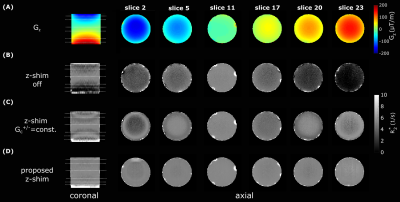
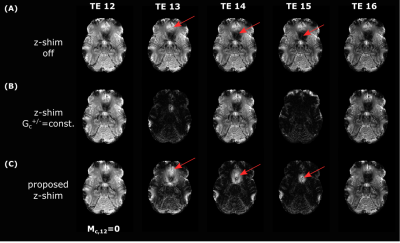
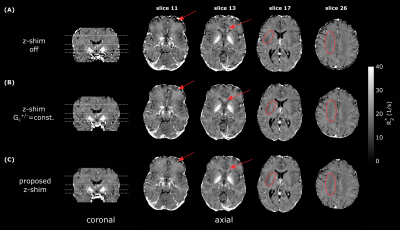
Figure 2 illustrates R2*-maps estimated with post-processing only (B), constant z-shim (C) and the proposed adaptive z-shimming (D). It clearly shows that R2* values in areas with increasing Gz are underestimated when using only the post-processing method. By application of constant z-shim gradients results are improved, especially in areas where |Gz| is around |Gc|=100µT/m (e.g. slice 5/20). In contrast, with the proposed method (D) homogenous R2* maps are obtained in the whole phantom. In Figure 3 images of the signal decays for the three different sequences are illustrated (slice 11;TE14-TE16). It shows that with the proposed approach the signal is successive rephased (arrows) in areas with strong Gz. Whereas without z-shim gradients the signal is already dephased in the same areas. Comparable in-vivo R2*-maps are shown in Figure 4. Post-processing corrected maps underestimate R2* values in areas with strong Gz (frontal cortex, arrow in slice 11) which can be improved by an application of Gc+/-. With the proposed adaptive slice-specific approach the contrast and SNR improves in areas with strong Gz (arrow in slice 11/13) and in areas with small Gz (circles in slice 17/26).

Discussion

We have developed a new method for adaptive slice-specific z-shimming for 2D mGRE sequences. Compared to a fixed compensation gradient scheme, the proposed approach reduces signal loss. Further, by splitting up Gc[n]+/- into three parts (1/3, 2/3, 3/3) a broader range of field gradients Gz is rephased (Figure 3). The proposed approach needs just a short (<25s) low-resolution pre-scan for estimating Gc[n]+/-. Interestingly, even in areas with relatively small |Gz|<50µT/m the adaptive approach outperforms the post-processing approach regarding SNR (Figure 3, slice 26/17).

Acknowledgements

This study was funded by the Austrian Science Fund (FWF grant numbers: KLI523, P30134) .

References

1.Fernández‐Seara MA, Wehrli FW. Postprocessing technique to correct for background gradients in image‐based R*2 measurements. Magn Reson Med. 2000;44(3):358-366. doi:10.1002/1522-2594(200009)44:3<358::AID-MRM3>3.0.CO;2-I

2. Preibisch C, Volz S, Anti S, Deichmann R. Exponential excitation pulses for improved water content mapping in the presence of background gradients. Magn Reson Med. 2008;60(4):908-916. doi:10.1002/mrm.21730

3. Hernando D, Vigen KK, Shimakawa A, Reeder SB. R2* mapping in the presence of macroscopic B0 field variations. Magn Reson Med. 2012;68(3):830-840. doi:10.1002/mrm.23306

4. Frahm J, Merboldt K-D, Hänicke W. Direct FLASH MR imaging of magnetic field inhomogeneities by gradient compensation. Magn Reson Med. 1988;6(4):474-480. doi:10.1002/mrm.1910060412

5.Yang QX, Williams GD, Demure RJ, Dardzinski BJ, Mosher TJ, Smith MB. Removal of local field gradient artifacts in GE images by slice excitation profile imaging (GESEPI) in high field. Magn Reson Med. 1998;39(3):402-409. doi:10.1002/mrm.1910390310

6. Truong T-K, Chakeres DW, Scharre DW, Beversdorf DQ, Schmalbrock P. Blipped multi gradient-echo slice excitation profile imaging (bmGESEPI) for fast T2* measurements with macroscopic B0 inhomogeneity compensation. Magn Reson Med. 2006;55(6):1390-1395. doi:10.1002/mrm.20916

7.Nam Y, Han D, Kim D-H. Single-scan R2⁎ measurement with macroscopic field inhomogeneity correction. Neuroimage. 2012;63(4):1790-1799. doi:10.1016/J.NEUROIMAGE.2012.08.062

8.Wen J, Cross AH, Yablonskiy DA. On the role of physiological fluctuations in quantitative gradient echo MRI: implications for GEPCI, QSM, and SWI. Magn Reson Med. 2015;73(1):195-203. doi:10.1002/mrm.25114

10. Soellradl M, Ropele R, and Langkammer C. Gradient echo modelling with macroscopic field variations and large flip angles. In Proceedings of the 27th Annual Meeting of ISMRM, Montreal, 2019

Figures

Figure 1: Overview of the compared sequences for R2*-mapping. In (A) a standard mGRE sequence with the same echo timings is shown. In (B) a z-shim pattern is illustrated where the moment for constant Gc+/- increases linearly with TE (dotted line) and is followed by rephasing (moments with same color). (C) shows the proposed slice-specific approach. For each slice a Gc[n]+/- is estimated in a pre-scan. In addition, Gc[n]+/- is split up with factors [1/3, 2/3, 3/3] followed by compensation of all moments. To correct for physiological fluctuation a navigator echo is acquired at TEnavi.

Figure 2: Estimated R2*-maps from a homogenous phantom estimated without z-shimming (B), with the constant Gc+/- (C) and with the proposed slice-specific approach (D). In addition, the field gradient map Gz is shown (A). Results indicate an underestimation of R2* values with post-processing only for strong |Gz|. With constant Gc+/- maps improved. The most homogenous and highest-SNR maps were obtained with the proposed approach.

Figure 3: Last four gradient echo images from TE12 to TE16 acquired with the sequence without z-shimming (A), with constant Gc+/-(B), and with the proposed slice-specific approach (C). At TE12 the sum of the compensation moments Mc,12 is zero. With the proposed approach different parts are subsequently rephased (arrows) in areas where the signal is already dephased without z-shim gradients (A).

Figure 4: Coronal and axial view of brain R2*-maps obtained without z-shimming (A), with constant Gc+/-(B), and with the proposed slice-specific approach (C). In areas with strong field gradients Gz (e.g. frontal cortex in slice 11) an improvement with z-shimming methods can be seen. Between (B) and (C) an improvement in SNR can be observed which is due to larger signal recovery.

Proc. Intl. Soc. Mag. Reson. Med. 28 (2020)
3152