Introduction

Myelin water imaging (MWI) is a non-invasive technique to estimate in-vivo myelin concentration (myelin water fraction, MWF) in a quantitative manner¹. Most of the MWI methods are based on the distinguishable relaxation time of myelin water. Thus, exponential-sum fitting is an essential part for accurate MWI. One of the popular approaches used for fitting a sum of exponential to measured signal is non-linear least-square (NLLS) technique^2–4. Due to the ill-posed condition of the exponential-sum fit, NLLS technique requires a proper initial guess for model parameters. Otherwise, the algorithm converges to an unacceptably poor fit⁵. In this work, we investigated the effects of parametric initial guess on MWI in both synthetic data and in-vivo measurement. We also proposed an MWI algorithm that is robust to initial guess by applying multiple initial guesses.

Methods

[Data acquisition]
2D multi-echo gradient-echo (GRE) sequence was used for MWI. The same scan protocols as our previous study were used⁶. To identify fiber orientation of the white matter, DTI with 6 directions were acquired with the same resolution.
[Signal model]
In this study, the following three pool complex model was used as a signal model⁴:$$S(t)=A_{my}exp(-\frac{t}{T_{2,my}^{*}}+i\cdot2\pi\cdot\Delta f_{my}t)+A_{ax}exp(-\frac{t}{T_{2,ax}^{*}}+i\cdot2\pi\cdot\Delta f_{ax}t)+A_{ex}exp(-\frac{t}{T_{2,ex}^{*}}).$$Here, A and $$${T_{2,my}^{*}}$$$ with the subscripts (my, ax, and ex represent myelin, axonal, and extracellular water) denote the amplitude and relative frequency shift.
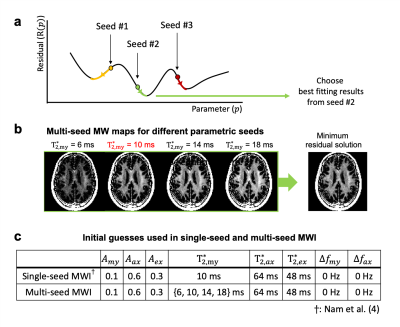
[Single-seed and multi-seed MWI algorithm]
To reduce errors originating from a single initial guess (=single-seed), a multi-seed MWI algorithm was proposed. The NLLS technique was repeatedly applied with different initial guesses of parameters (=multi-seed). Based on the hypothesis that $$${T_{2,my}^{*}}$$$ has the largest effects on MWI, only the initial seed of $$${T_{2,my}^{*}}$$$ was varied from the single seed parameters. Then, the fitting result with minimum residual was chosen voxel-wise (Fig. 1). Parameter sets are summarized in Fig 1c.
[Experiment 1: effects of initial seed on in-vivo MWI]
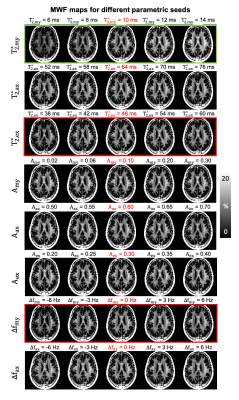
To investigate the effects of each parametric seed on MWF, MWF maps were generated with different initial seed sets (Fig. 2).
[Experiment 2: exponential-sum fit to synthetic data]
To investigate the ill-conditioned nature of the exponential-sum fit, single- and multi-seed methods were applied to synthetic data. Synthetic GRE signals with different $$${T_{2,my}^{*}}$$$ were simulated using three pool complex exponential model (Fig. 3a). To assume practical conditions of $$${T_{2,my}^{*}}$$$ values, Gaussian noise was added to make SNR of 300. Single- and multi-seed MWI methods were applied to the noisy signals. This procedure was repeated 1000 times and the results were averaged.
[Experiment 3: exponential-sum fit to in-vivo measurement]
NLLS fitting with single- and multi-seed MWIs were applied to the in-vivo multi-echo GRE measurement. To explore the effects of appropriate initial seed of $$${T_{2,my}^{*}}$$$, we observed the dependency of MWI results on fiber orientation. This is because fiber orientation can be a surrogate measure of $$${T_{2,my}^{*}}$$$². MWF and $$${T_{2,my}^{*}}$$$ were estimated for different fiber orientations using both single- and multi-seed methods. In addition, $$${T_{2,my}^{*}}$$$ values for different fiber orientations were simulated using the hollow cylinder model⁷ and compared to the in-vivo measurement. The same parameters (except for field strength; 3T) described in Sati et al.’s work was used for the simulation². For quantitative comparison between the single- and multi-seed MWI, region of interest (ROI) analyses were performed in four manually defined ROIs (Fig. 5).

Results

When the effects of each parametric seed were assessed, $$${T_{2,my}^{*}}$$$ has the most significant impact on MWF values when compared to that from other parameters (Fig. 2). This result validates our hypothesis that $$${T_{2,my}^{*}}$$$ has the largest effects on MWF out of 8 fitting parameters.
Fig. 3 compares the effects of single- and multi-seed algorithm in the simulation. When the single-seed algorithm was applied, errors in estimated MWF and $$${T_{2,my}^{*}}$$$ tend to increase when the difference between initial guess and assigned $$${T_{2,my}^{*}}$$$ value is larger (Figs. 3b,c). In contrast, the results from multi-seed MWI agree with the true MWF and $$${T_{2,my}^{*}}$$$ values regardless of assigned $$${T_{2,my}^{*}}$$$ (Figs. 3b,c). These results validate the theoretical effectiveness of multi-seed algorithm.
Fig. 4 shows the effects of the single- and multi-seed algorithms in in-vivo measurement. Compared to result from single-seed, multi-seed MWI demonstrates lower dependency of MWF on fiber orientation (Figs. 4a, c). Estimated $$${T_{2,my}^{*}}$$$ has fiber-orientation dependency (Figs. 4b,d), which is analogous to that of the hollow cylinder model (Fig. 4e).
ROI analysis (Fig. 5) reveals significantly increased values of MWF and $$${T_{2,my}^{*}}$$$ in B₀-parallel fiber (PLIC) when the multi-seed algorithm is used. These findings are well matched with previous studies which reported large MWF in this region^8,9. On the other hand, regions with B₀-perpendicular fibers (SPL, SLF) show no significant difference between the single- and multi-seed algorithms except for the region with a large B₀ field inhomogeneity (GENU) (Fig. 5). The results show the necessity of different initial seeds for different white matter regions.

Conclusion

In this work, we explored the effects of initial guess on the exponential-sum fit of MWI and suggested a plausible solution to reduce initial guess-dependnet error by applying multi-seed algorithm. The results revealed that proper initial guess is essential for myelin quantification. Since we only focused on a parameter ($$${T_{2,my}^{*}}$$$) which shows the most significant impact, further study may be needed to explore effects of other parameters.