3137

Accelerated quantitative magnetization transfer (qMT) imaging using compressed sensing and parallel imaging

Melany McLean¹, R. Marc Lebel^1,2, M. Ethan MacDonald¹, Mathieu Boudreau^3,4, and G. Bruce Pike¹
¹Departments of Radiology and Clinical Neuroscience, Hotchkiss Brain Institute, University of Calgary, Calgary, AB, Canada, ²GE Healthcare, Calgary, AB, Canada, ³Montreal Heart Institute, Université de Montreal, Montreal, QC, Canada, ⁴NeuroPoly Lab, Institute of Biomedical Engineering, Polytechnique Montreal, Montreal, QC, Canada

Synopsis

Quantitative magnetization transfer (qMT) is a Z-spectrum based imaging technique used to study white matter. The need to acquire many images with unique RF saturation pulses leads to long acquisition times. We aim to shorten qMT imaging times using a sparseSENSE technique that combines parallel imaging and compressed sensing to reduce the amount of acquired data. Retrospectively undersampled data was reconstructed for a range of acceleration factors using wavelet and total variation sparsifying domains. Pool size ratio (F) maps were accelerated by a factor of 4×, and acceleration factors of 8-12× may be possible in future work.

Introduction

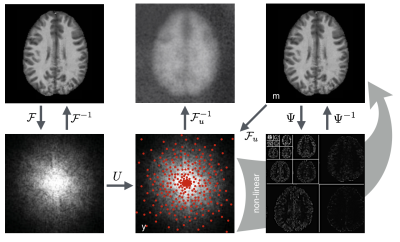
Quantitative magnetization transfer (qMT)¹ is an MRI technique that measures an index of myelin content in brain white matter (WM).^2,3 Macromolecules, including those which make up myelin, cannot be directly measured with conventional MRI techniques due to sub-millisecond T₂ times.⁴ qMT fits data to the magnetization exchange model⁵ between pools of restricted (macromolecular) and free (liquid) protons, thereby indirectly measuring the macromolecular pool. The MT-prepared spoiled gradient echo technique¹ (MT-SPGR) used in this work creates MT-saturation by applying an additional off-resonance RF-pulse to selectively saturate restricted hydrogen nuclei. By repeating the acquisition many times with unique off-resonance pulses, signal changes can be plotted to produce a characteristic curve, known as the Z-spectrum, to which the two-pool qMT model is fit. The need to acquire many images leads Z-spectrum based imaging techniques, including qMT and chemical exchange saturation transfer (CEST), to suffer from long acquisition times.

The aim of this work is to shorten qMT imaging times using a combined compressed sensing (CS) and parallel imaging (PI) method, sparseSENSE.⁶ PI uses multiple receive coils with unique spatial sensitivity profiles to provide additional spatial information, reducing the data sampling requirements.⁷ CS reduces data acquisition time by undersampling k-space and using an iterative nonlinear image reconstruction algorithm. Figure 1 depicts how sparsifying transform domains, in combination with random sampling trajectories, are used to reconstruct high fidelity images with undersampled data.⁸

Methods

3D qMT data was collected using an SPGR sequence with Gaussian shaped MT-saturation pulses. Ten MT-saturated images were collected using two MT pulse powers and five logarithmically spaced offset frequencies.⁹ A baseline image with no MT pulse, B₀ and B₁ field maps, and a T₁-map were acquired to constrain the qMT model¹ and correct for field variations.

Data was acquired in five healthy subjects using a 3.0T GE Discovery-MR750 scanner and a 32-channel head coil. Raw k-space was stored as a 5D dataset with 128×128×96 spatial matrix, 11 MT-offsets, and 32 channel images for PI. Pseudo-random retrospective under-sampling was performed in the phase, slice, and MT-offset dimensions. Undersampling was performed using a Poisson-disc sampling strategy while enforcing a probability density function of $$$f(r)=1/r^d$$$ , where r is the distance to the centre of k-space and $$$d=2$$$.¹⁰ A fully sampled circular core of k-space containing 10% of the total samples was included to account for the energy distribution of k-space.

Image reconstruction was performed by solving: $$$f(m)=||F_uSm-y||_2^2+λ_1||m-m_r||_1+λ_2||Ψm||_1+λ_3||TVm||_1$$$ using the nonlinear conjugate gradient method, where Ψ and TV are the wavelet and total variation sparsifying transforms respectively. F_u is the under-sampled Fourier transform and S is the coil sensitivity operator for PI. m_r is a local low-rank reference image to promote simple behaviour in the frequency-offset dimension. Regularization parameters were set to λ₁=0.005, λ₂=0.0005, and λ₃=0.0001. Undersampling was performed at eight acceleration factors evenly spaced between 4× and 32×. Using qMRLab,¹¹ qMT parameter maps were fit to undersampled data using the Sled & Pike approximations¹ to numerically solve the MT-exchange equations.

Results

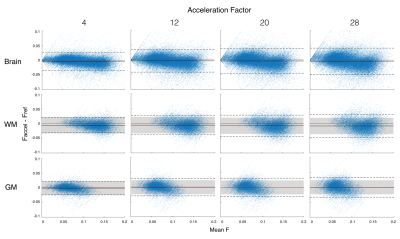
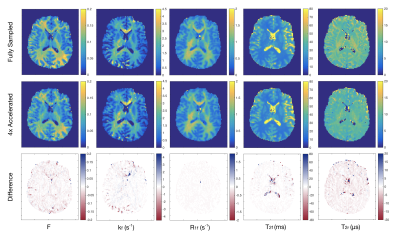
Of the qMT parameters, the pool size ratio (F) is most strongly correlated to myelin content in brain WM^2,3,9 and is therefore the primary focus of this analysis (Fig.2). A Bland-Altman analysis¹² was used to compare accelerated and fully sampled F-maps (Fig.3). Bias between the two reconstruction methods was determined using the mean of differences between voxels (y-axis). In this study, we compare bias in accelerated images to the coefficient of variation (CoV) observed in repeated, fully sampled, qMT scans in healthy adults.¹³ Overall agreement is reported using the standard deviation (SD) of differences between the two methods, known as the limits of agreement (LOA). Acceptable LOA were defined as those that do not exceed the pooled SD of fully sampled data for a given region of interest (ROI).

Discussion

We previously showed that individual MT-weighted images and Z-spectra can handle ambitious acceleration factors, with minimal reconstruction artefacts at acceleration factors exceeding 12×.¹⁴ In the present work, we found that qMT parameter maps are more sensitive to acceleration artefacts than the input data. For both WM and grey matter (GM), an acceleration factor of 4× yielded acceptable agreement with fully sampled F-maps (Tab.1). This acceleration factor yields typical qMT parametric maps shown in Figure 4.

The next step of this work is to implement undersampling strategies prospectively to yield real acquisition time savings. Due to the initial results in raw MT-weighted images and accelerated Z-spectra,¹⁴ a wide range of acceleration factors with large increments between them was examined. qMT parametric maps are more sensitive to acceleration artefacts, therefore acceleration factors ranging between 4× and 8× should be experimentally evaluated in prospective work.

Conclusion

The SPGR qMT model was shown to be sensitive to small Z-spectrum changes induced by image acceleration. The true limits of image acceleration will come from future studies that implement this accelerated acquisition technique prospectively; however, these findings suggest that acceleration factors of 4× are likely possible, and that acceleration factors up to 8-12× should be explored. With the current work supporting the use of an acceleration factor of at least 4×, qMT acquisition time can be reduced from 28 minutes to under 7 minutes, helping to make qMT a clinically feasible imaging tool.

Acknowledgements

The authors would like to recognize financial support from the Canadian Institutes of Health Research (FDN 143290) and the Campus Alberta Innovates Program.

References

1. Sled JG, Pike GB. Quantitative Interpretation of Magnetization Transfer in Spoiled Gradient Echo MRI Sequences. J. Magn. Reson. 2000;145(1):24-36.

2. Sled JG, Levesque IR, Santos AC, et al. Regional variations in normal brain shown by quantitative magnetization transfer imaging. Magn. Reson. Med. 2004;51(2):299-303.

3. Kucharczyk W, Macdonald PM, Stanisz GJ, et al. Relaxivity and magnetization transfer of white matter lipids at MR imaging: importance of cerebrosis and pH. Radiology. 1994;192(2)521-529.

4. Cercignani M, Barker GJ. A comparison between equations describing in vivo MT: The effects of noise and sequence parameters. J. Magn. Reson. 2008;191(2):171-183.

5. Henkelman RM, Huang X, Xiang QS, et al. Quantitative interpretation of magnetization transfer. Magn. Reson. Med. 1993;29(6):795-766.

6. Liu B, Zou YM, Ying L. Sparsesense: Application of compressed sensing in parallel MRI. 5th Int. Conf. Inf. Technol. Appl. Biomed, Shenzhen. 2008;127-130.

7. Pruessmann KP, Weiger M, Scheidegger MB, et al. SENSE: Sensitivity encoding for fast MRI. Magn. Reson. Med. 1999;42(5):952-962.

8. Jaspan ON, Fleysher R, Lipton ML. Compressed sensing MRI: A review of the clinical literature. Br. J. Radiol. 2015;88(1056):1-12.

9. Levesque IR, Sled JG, Pike GB. Iterative optimization method for design of quantitative magnetization transfer imaging experiments. Magn. Reson. Med. 2011;66(3):635-643.

10. Zijlstra F, Viergever MA, Seevinck PR. Evaluation of variable density and data-driven K-space under sampling for compressed sensing magnetic resonance imaging. Invest. Radiol. 2016;51(6):410-419.

11. Cabana JF, Gu Y, Boudreau M, et al. Quantitative magnetization transfer imaging made easy with qMTLab: Software for data simulation, analysis, and visualization. Concepts. Magn. Reson. 2015;44A(5):263-277.

12. Bland JM, Altman DG. Statistical Methods for Assessing Agreement Between Two Methods of Clinical Measurement. The Lancet. 1986;327(8476):307-310.

13. Levesque IR, Sled JG, Narayanan S, et al. Reproducibility of quantitative magnetization-transfer imaging parameters from repeated measurements. Magn. Reson. Med. 2010;64(2):391-400.

14. Mclean M, Macdonald ME, Lebel RM, et al. Accelerated Z-spectrum imaging. 25th Conf. Int. Soc. Magn. Reson. Med, Honolulu. 2017.

Figures

Fig. 1. Domains and transform operators used in typical image reconstruction (left column), a simple under-sampled reconstruction (middle column), and CS reconstruction (shaded arrow). m and y represent the reconstructed image and measured k-space data (red dots) respectively. U is the undersampling operator, F_u is the under-sampled Fourier transform, and Ψ is the wavelet transform. Using iterative reconstruction, CS is able to produce a final image (m) that closely resembles fully sampled data (top left).

Fig. 2. Accelerated F-maps (a) and difference images (b) from one healthy subject. Acceleration factors are indicated on the x-axis, where fully sampled data has an acceleration factor of 1. Negative differences indicate underestimated voxels in accelerated F-maps. Arrow A indicates areas of overestimated F voxels in fully sampled data, correlated with areas of large differences in accelerated data. Key acceleration artifacts include voxels in ventricles with a high F value (arrow B) and ringing artifact at higher acceleration factors (arrow C).

Fig. 3. Bland-Altman plots for accelerated F-maps in all brain voxels (top row), and in ROIs of WM (middle row) and GM (bottom row). Plots summarize data from 5 subjects, reconstructed with 4 unique sampling trajectories for each acceleration rate. Solid black lines indicate mean differences between pairs of voxels in fully sampled and accelerated images (red lines = 0). Dashed lines indicate limits of agreement (±1.96 SD), with reference values indicated by the shaded regions.

Table 1. Summary of Bland-Altman statistical analysis. Each row corresponds to one statistical measure and its method of comparison. Mean differences (ΔF) are compared to longitudinal coefficients of variation (CoV) within healthy subjects¹³. Mean CoVs were approximately 5% in F, averaged over data collected in multiple ROIs. This variation corresponds to F differences of 0.64% in WM and 0.34% in GM. Limits of agreement (LOA / σ_F) are compared to the within ROI SD of fully sampled F-maps, pooled across subjects. Fully sampled data was found to have a pooled SD of 2.8% in WM and 2.4% in GM.

Fig. 4. The complete set of qMT parameter maps based on the two-pool tissue model⁵produced in one healthy subject using fully sampled data (top row) and retrospectively under-sampled data at an acceleration factor of 4× (middle row). Differences between the two methods are shown in the bottom row. Columns represent the pool-size ratio (F), magnetization exchange rate from free to restricted pool (k_r), longitudinal relaxation rate of the free pool (R_1f), and transverse relaxation times of free (T_2f) and restricted (T_2r) pools.

Proc. Intl. Soc. Mag. Reson. Med. 28 (2020)

3137