3132
qMTNet: Accelerated Quantitative Magnetization Transfer Imaging with Neural Networks1Bio and Brain Engineering, Korea Advanced Institute of Science and Technology, Daejeon, Republic of Korea, 2Department of Radiology, Seoul National University Hospital, Seoul, Republic of Korea
Synopsis
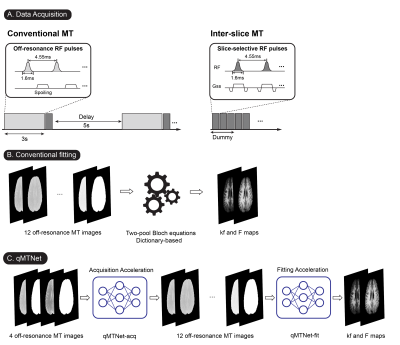
Quantitative magnetization transfer (qMT) imaging overcomes the drawbacks of traditional MT imaging by producing more quantitative parameters. However, data acquisition and processing can be time-consuming, which limits its usage. In this study, an artificial neural network, qMTNet, is proposed to accelerate both the acquisition and fitting of qMT data. For data acquired from both conventional and inter-slice acquisition strategies, our approach demonstrated consistent fitting results with those from a previous dictionary-driven fitting method. The network reduces the time for both data acquisition and qMT fitting by a factor of 3 and 5000 times, respectively, compared to the conventional methods.
Introduction
Quantitative magnetization transfer imaging (qMT) promises improvements in consistency and accuracy of estimated parameters over conventional magnetization transfer ratio imaging. qMT has been applied for clinical usages such as multiple sclerosis [1] or post-therapy glioblastoma monitoring [2]. However, conventional qMT requires long acquisition time for sufficient saturation of the pools as well as lengthy post-processing time to fit the modified Bloch equation for each voxel. Although recent researches proposed strategies to accelerate data acquisition and fitting [3], there is still a lot of room for improvement.Advances in deep learning have enabled significant improvement in processing time and quality of MR images for tasks like MR acceleration, over more traditional methods such as compressed sensing [4,5]. In this study, we propose qMTNet, a neural network that composes of two sub-neural-networks to accelerate the qMT workflow. The first subnetwork, qMTNet-acq, produced the complete MT acquisition from a small subset of acquired data. The second network, qMTNet-fit, maps the MR signals to the qMT parameters. qMTNet is the combination of these two subnetworks and demonstrated significant improvement in data acquisition and processing time over the previous methods while maintaining consistent qMT maps.
Methods
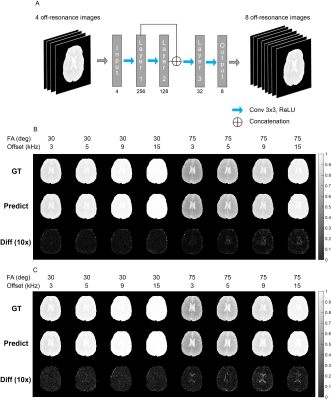
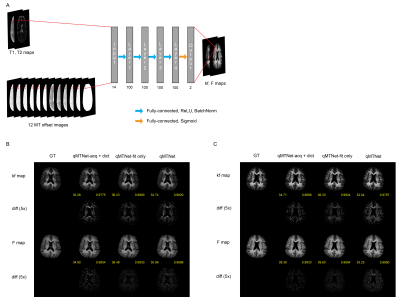
Imaging experiments were performed on 8 subjects, with approval from the local Institutional Review Board. Experiments and processing of data were carried out following the protocols described in [3]. In short, conventional [6] and inter-slice MT acquisition [7,8] with bSSFP readout (Figure 1A) was performed with a 3T scanner (Tim Trio, Siemen) at two flip angles (30°, 75°) and six off-resonance frequencies (2, 3, 5, 9, 15, 25 kHz) [9]. T1 and T2 values were mapped using inversion recovery and multi-echo spin echo sequence. qMT parameters (Magnetization exchange rate (kf) and pool ratio (F)) were fitted with the dictionary-driven method in [3].Each subnetwork of qMTNet was trained separately, with different design considerations. The first subnetwork, termed qMTNet-acq, seeks to accelerate the qMT acquisition by predicting the missing 8 MT offset images from 4 acquired images. qMTNet-acq subnetwork operated on the whole image and consisted of 4 3x3 convolutional layers with ReLU activation (Figure 2A). The convolutional layers allowed the network to generate more consistent local structures. The second subnetwork, called qMTNet-fit, performed the fitting process by learning the mapping between voxels’ MT intensities and the qMT parameters. qMTNet-fit subnetwork had 4 fully-connected layers with ReLU and batch normalization. The network operated in a pixelwise manner to conform to the conventional fitting method. qMTNet is the combination of qMTNet-acq and qMTNet-fit, producing qMT parameters directly from under-sampled qMT data.
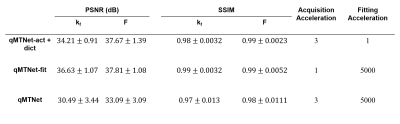
Cross validation was performed with 7 subjects. Data from 1 subject was removed due to motion artefact. Each subnetwork was trained separately with the appropriate data. The performance of qMTNet-acq was assessed by comparison of predicted and experimentally-acquired MT images. qMT parameters from 3 fitting procedures: predicted MT images from qMTNet-acq fitted with dictionary fitting, fully acquired data fitted with qMTNet-fit, and qMTNet (i.e: qMTNet-acq + qMTNet-fit) were compared quantitatively in term of PSNR and SSIM metrics and qualitatively by visual inspection against the ground truth from dictionary fitting with fully acquired data.
Result
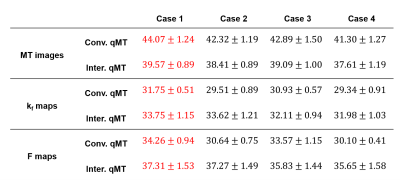
Different input offset frequencies were considered for the qMTNet-acq. As shown in Table 1, inclusion of the first and last offset frequencies for each flip angle produced the best prediction with respect to PSNR metric, which could be attributed to the fact that this combination provided the network with a larger range of off-resonance frequencies for learning to predict the missing MT offset images. Qualitative comparison of the fitting results for an exemplary slice can be seen in Figure 3B. qMTNet-fit showed better visual consistency and quantitative values in PSNR and SSIM with respect to the ground truth than qMTNet-acq + dictionary or qMTNet. This is because qMTNet-fit was trained and tested on the 12 MT images rather than the reduced 4 MT images. Although less accurate, the PSNR and SSIM values were acceptable for the qMTNet-acq + dictionary and qMTNet as they are both above 30 and 0.98, respectively. qMTNet performed slightly worse than qMTNet-acq for inter-slice data but better for conventional data, possibly due to the amount of training data for qMTNet-acq. Quantitative fitting results (Table 2) of different combinations of subnetworks agree with the qualitative observation. qMTNet-fit produced the best result, followed by qMTNet-acq and qMTNet. As a trade-off, qMTNet demonstrates the highest acceleration factor over previous methods with 3 fold acceleration in acquisition time and over 5000 fold acceleration in fitting time.Discussion
qMTNet significantly accelerates qMT imaging for both acquisition and fitting processes while producing consistent outputs. For a fair comparison, all methods were processed with the same CPU. Even higher acceleration will be possible with the use of GPU. The modular nature of qMTNet enables its usage in various scenarios. qMTNet can be utilized to accelerate the whole qMT process from acquisition to fitting and each of its subnetworks can be flexibly integrated into different settings which might require acceleration in only one of the two steps. The utility of qMTNet should be further investigated with more diverse data including patients' data which might show qMT values different from those of healthy subjects.Acknowledgements
No acknowledgement found.References
[1] van Buchem MA, McGowan JC, Kolson DL, Polansky M, Grossman RI. Quantitative volumetric magnetization transfer analysis in multiple sclerosis: Estimation of macroscopic and microscopic disease burden. Magn Reson Med. 1996;36:632–636.
[2] Mehrabian H, Myrehaug S, Soliman H, Sahgal A, Stanisz GJ. Quantitative magnetization transfer in monitoring glioblastoma (GBM) response to therapy. Sci Rep. 2018;8:2475.
[3] Kim, J‐W, Lee, S‐L, Choi, SH, Park, S‐H. Rapid framework for quantitative magnetization transfer imaging with interslice magnetization transfer and dictionary‐driven fitting approaches. Magn Reson Med. 2019; 82: 1671– 1683.
[4] Han, Y., Sunwoo, L., & Ye, J. C. (2019). k-Space Deep Learning for Accelerated MRI. IEEE Transactions on Medical Imaging.
[5] Lee, J, Han, Y, Ryu, J-K, Park, J-Y, Ye, JC. k‐Space deep learning for reference‐free EPI ghost correction. Magn Reson Med. 2019; 82: 2299– 2313
[6] Henkelman RM, Huang X, Xiang QS, Stanisz GJ, Swanson SD, Bronskill MJ. Quantitative interpretation of magnetization transfer. Magn Reson Med. 1993;29:759–766.
[7] Barker JW, Han PK, Choi SH, Bae KT, Park SH. Investigation of inter‐slice magnetization transfer effects as a new method for MTR imaging of the human brain. PLoS ONE. 2015;10:e0117101.
[8] Han PK, Barker JW, Kim KH, Choi SH, Bae KT, Park S‐H. Inter‐slice blood flow and magnetization transfer effects as a new simultaneous imaging strategy. PLoS ONE. 2015;10:e0140560.
[9] Cercignani M, Alexander DC. Optimal acquisition schemes for in vivo quantitative magnetization transfer MRI. Magn Reson Med. 2006;56:803–810.
Figures