3129

Turnkey qMT via Selective Inversion Recovery
Richard Dortch1
1Division of Neuroimaging Research, Barrow Neurological Institute, Phoenix, AZ, United States

Synopsis

MTR offers a measure of myelin content, but is also sensitive to non-physiological parameters. Quantitative MT methods remove these confounding effects; however, they require long scan times and complicated acquisition/analysis strategies. Selective inversion recovery is a simple method that may address many of these limitations, but requires long scan times and specialized inversion recovery sequences. The issue of long scan times was previously addressed through optimized sampling schemes. The need for specialized sequences is addressed herein by using a standard MP-RAGE sequence and modifying the SIR signal model. The resulting “turnkey” approach was tested numerically and applied in the brain.

Introduction

The magnetization transfer ratio (MTR) offers a rapid and straightforward measure that is indicative of myelin content1. Unfortunately, MTR is also sensitive to non-physiological parameters and tissue relaxation times2, challenging standardization across sites/vendors and time. Quantitative MT (qMT) methods3-5 have been developed to remove these confounding effects and yield indices with a higher degree of tissue-specificity (e.g., the macromolecular-to-free proton pool-size-ratio, or PSR); however, they require long scan times and complicated acquisition/analysis strategies that are unavailable on most clinical systems. Selective inversion recovery (SIR) is an alternative qMT method that may address these limitations because it simplifies the acquisition/analysis associated with standard qMT methods (e.g., it does not require estimates of ∆B0, B1+, or T1). The drawbacks of SIR are: i) the long scan times required to obtain data at multiple inversion times and ii) the need for specialized inversion recovery sequences that saturate (or “reset”) the longitudinal magnetization of both pools at the end of the readout, which simplifies the signal model for shorter-TRs. The issue of long scan times was previously addressed through optimized sampling schemes and data reduction strategies6; and more recent data7 indicate that further reductions in scan times are feasible through efficient 3D readouts and SENSE acceleration in multiple directions. The need for specialized sequences is addressed herein by using a standard magnetization-prepared rapid gradient-echo (MP-RAGE) sequence (i.e., no “reset” pulses) and modifying the signal model to account for the non-zero steady-state longitudinal magnetization at the end of each readout. The resulting “turnkey” approach was tested numerically and applied in the brain of a healthy subject.

Theory

The primary difference between the conventional and turnkey SIR methods are that the former uses a “reset” train of RF pulses to saturation the longitudinal magnetization of both pools (Fig. 1), which simplifies the signal model when tD<5*T1. With the “reset” pulses (Mz(tD=0)=0), the SIR signal model can be given by6

Mz(tI,tD) = {exp(AtI)S[I - exp(AtD)] + [I - exp(AtI)])}M0,

where tI and tD are defined in Fig. 1, Mz=[Mzf Mzm]T is the longitudinal magnetization vector, I is the identity matrix, M0=[M0f M0m]T is a vector of equilibrium magnetizations, S=diag(Sf, Sm) accounts for the effect of the inversion pulse on each pool (Sf=−1 indicates complete inversion of Mzf, Sm=1 indicates no saturation of Mzm), and the matrix A defines the R1 of each pool and the rate of MT exchange between pools. Removal of the “reset” pulses (Mz(tD=0)≠0), results in a more complicated model that can be derived by expanding the steady-state solution for the MP-RAGE sequence8 from one pool to two pools

Mz,ss(tI,tD) = [I - EDBNEISI]-1{ED[BN(I - EI) + (I - B)-1(I - BN)(I - ER)] + (I - ED)}M0,

where N is the number of excitation pulses in the MP-RAGE readout, SI,E accounts for the saturation of the inversion and excitation pulses, EI,D,R=exp(AtI,D,R), tR is the spacing between each excitation pulse in the readout, and B=SEER.

Methods

For numerical validation, the solutions to the two-pool ODEs describing the system were propagated through each segment of the pulse sequence in Fig. 1 until steady-state was obtained, and the resulting signal was compared to the analytical solution. In addition, Monte Carlo simulations were performed over 2000 unique noise realizations (SNR at thermal equilibrium=2000) to compare the precision of PSR estimates6 from conventional and turnkey SIR. Additional parameters included: TE/tR=1.3/2.6 ms, flip angle=5˚, inversion pulse Sm/Sf=0.83/-1.0, excitation pulse Sm/Sf=1.0/cos(5˚), N=48, PSR=15%, MT exchange rate (kmf)=15s-1, and R1=1 s-1 for both pools.

For experimental validation, 3D SIR data were acquired with and without the “reset” pulses in the brain of healthy subject, and PSR estimates6 from each method were compared. MRI data were acquired using a 3T Achieva MRI scanner (Philips), a 32-channel head coil, and the imaging parameters listed for the simulations. Additional parameters included: center-out k-space trajectory in kx-ky (linear in kz), FOV=211x211x99 mm3, resolution=2.2x2.2x3 mm3, SENSE acceleration=2x2, and NEX=1.

Results and Discussion

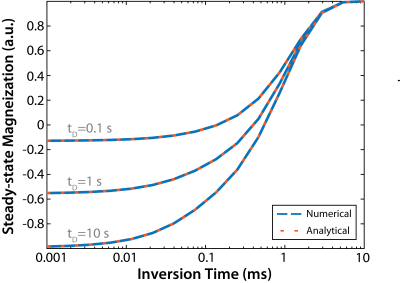
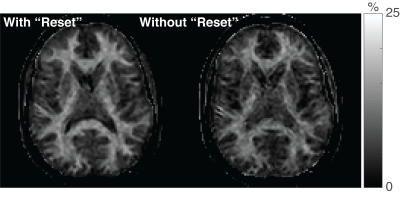
Figure 2 shows that the ODEs and the analytical expression described above yield identical results. For all tI/tD values, the difference between the transient and steady-state signal was less than 0.01% after three repetitions, indicating that dummy scans are not required for 3D readouts with linear ordering in kz. For the Monte Carlo simulations, an SNR of 17.6 and 15.3 was observed for PSR estimates using the conventional and turnkey SIR methods, respectively. In other words, both methods yielded similar levels of precision, although the turnkey methods did result in an acceptable 13.1% reduction in SNR. Figure 3 shows PSR maps from a single-slice using both SIR methods. In agreement with the numerical results, both methods yielded similar PSR values, although the SNR of the PSR map from the turnkey method was slightly reduced.

Conclusions

SIR data can be robustly acquired using a standard, clinically avaliable MP-RAGE sequence at four different inversion times. This removes the need for specialized pulse sequence programming, which is a bottleneck in clinical translation. Future work will focus on evaluating the effect of i) B1+ errors, ii) different k-space trajectories and flip angle schedules for the MP-RAGE readout, and iii) inversion pulse shape/power. In addition, the method will be applied in patients with multiple sclerosis.

Acknowledgements

Funding provided by NIH R01 NS09782.

References

  1. Odrobina EE, Lam TY, Pun T, Midha R, Stanisz GJ. MR properties of excised neural tissue following experimentally induced demyelination. NMR Biomed. 2005;18:277-284.
  2. Berry I, Barker GJ, Barkhof F, et al. A multicenter measurement of magnetization transfer ratio in normal white matter. J Magn Reson Imag. 1999;9:441-446.
  3. Gochberg D and Gore JC. Quantitative magnetization transfer imaging via selective inversion recovery with short repetition times. Magn Reson Med. 2007;57:437-441.
  4. Sled JG and Pike GB. Quantitative interpretation of magnetization transfer in spoiled gradient echo MRI sequences. J Magn Reson. 2000;145: 24-36.
  5. Gloor M, Scheffle, K, and Bieri O. Quantitative magnetization transfer imaging using balanced SSFP. Magn Reson Med. 2008;60:691-700.
  6. Dortch RD, Bangato F, Gochberg DF, Gore JC, and Smith SA. Optimization of selective inversion recovery magnetization transfer imaging for macromolecular content mapping in the human brain. Magn Reson Med. 2018;80:1824-1835.
  7. Cronin MJ, Junzhong X, Gochberg DF, and Dortch RD. Optimization and acceleration of selective Iinversion recovery imaging for practical whole-brain quantitative magnetization transfer measurements. At: 26th Annual Meeting of ISMRM, Paris, June, 2018.
  8. Marques JP, Kober T, Krueger G, Zwaag W, Moortele PF, and Gruetter R. MP2RAGE, a self bias-field corrected sequence for improved segmentation and T1-mapping at high field. Neuroimage. 2010;49:1271-1281.

Figures

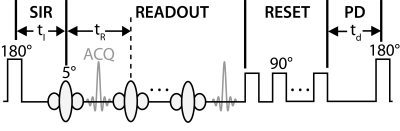
Figure 1. RF pulse diagrams for the traditional SIR method. The sequence employs a 1-ms hard inversion pulse followed by a variable delay inversion recovery period (tI) to sample the biexponential recovery of longitudinal magnetization, an MP-RAGE readouts with acquisitions (ACQ) spaced at tR, a train of “reset” RF pulses to saturate the water/macromolecular longitudinal magnetization at tD=0, and a predelay (PD) to allow for partial recovery of magnetization. The turnkey method removes the series of "reset" pulses, in which case tD=0 is defined at the end of the readout .


Figure 2. Evolution of steady-state magnetization for the turnkey SIR method derived from numerical (solution to ODEs) and analytical expressions. Identical results were found using both methods over a large range of tI and tD values, numerically confirming the analytical model.

Figure 3. PSR maps acquired with/without the “reset” pulse. Similar PSRs were obtained in both, experimentally confirming the model. The lower SNR for the turnkey method (without "reset") scan can be partially attributed to that fact that the acquisition was optimized for the traditional SIR method.

Proc. Intl. Soc. Mag. Reson. Med. 28 (2020)
3129