3111
Induced Saturation Transfer Recovery Steady State (iSTRESS) for proton exchange rate imaging with MRI
Mehran Shaghaghi1 and Kejia Cai1,2,3
1Radiology, University of Illinois - Chicago, Chicago, IL, United States, 2Bioengineering, University of Illinois - Chicago, Chicago, IL, United States, 3Center for MR Research, University of Illinois - Chicago, Chicago, IL, United States
1Radiology, University of Illinois - Chicago, Chicago, IL, United States, 2Bioengineering, University of Illinois - Chicago, Chicago, IL, United States, 3Center for MR Research, University of Illinois - Chicago, Chicago, IL, United States
Synopsis
We present a novel method to induced saturation-transfer-recovery steady-states for determining proton exchange (kex) with low saturation power, short duration, and hence negligible SAR deposition. Our previous study has demonstrated that omega plotting with direct saturation (DS) signal removed can be used to map kex of healthy brains in vivo. However, omega plot, based on steady-state saturation assumption, requires long scanning time and potential high SAR deposition, which makes it non-applicable for clinical studies. Our suggested method, validated by simulations and phantom imaging, shows great promise for in vivo proton exchange rate imaging and clinical applications.
Background and Purpose
Proton exchange is the fundamental mechanism underpinning CEST MRI contrast, and it has been reported that mapping of the proton exchange rate (kex) may help the clinical diagnosis of stroke and cancer [1, 2]. Our preliminary study has demonstrated that omega plotting with direct saturation (DS) signal removed can be used to map the exchange rate in healthy brains in vivo [3]. However, omega plot based on steady-state saturation assumption may lead to long scanning time and potential high SAR deposition, limiting it from clinical applications. Here we propose a novel method with induced saturation-transfer-recovery steady states (iSTRESS) to measure kex with low saturation power, short duration, and hence negligible SAR deposition.Theoretical considerations and methods
Continuous RF saturation on a metabolite’s chemical shift frequency reduces its signal. For an RF with the power B1, the saturation efficiency, $$$α$$$, can be approximated as [4-7]: $$α= \frac{(γB_1)^2}{(γB_1)^2+(k_{ex})^2 }{\phantom \cosin} (1)$$in which $$$\gamma$$$ is the nuclear gyromagnetic ratio (42.58 Hz/µT for proton).
Proton exchange between the metabolite and bulk water pool transfers a portion of saturated protons to the water pool and cause its signal to reduce. The rate of signal loss in the water pool due to the exchange with the saturated protons from the metabolite’s pool depends on the exchange rate, the relative proton density ($$$f$$$), as well as the saturation efficiency: $$R_{exch}=k_{ex}×f×α{\phantom \cosin} (2)$$
Concurrently, the signal of water pool protons recovers back towards its equilibrium value due to the inherent spin-lattice relaxation (T1-recovery) process with the rate of $$$\left(1-\frac{M_{Z,ss}^A}{M_{Z,eq}^A}\right)R_1^A$$$, where $$$M_{Z,ss}$$$ and $$$M_{Z,eq}$$$ are the steady-state and the equilibrium magnetization respectively, and $$$R_1=1/T_1$$$. In a saturation transfer recovery steady-state (STRESS) (Fig.1), when the signal loss due to the proton exchange balances the signal gain due to the T1 recovery, the signal stays at a steady-state value. Therefore, under STRESS we have $$\frac{M_{Z,ss}^A}{M_{Z,eq}^A}×R_{exch} =\frac{M_{Z,ss}^A}{M_{Z,eq}^A}×k_{ex}×f×\frac{(γB_1)^2}{(γB_1)^2+(k_{ex})^2 }=\left(1-\frac{M_{Z,ss}^A}{M_{Z,eq}^A}\right)R_1^A{\phantom \cosin} (3)$$ where $$$M_{Z,ss}$$$, $$$M_{Z,eq}$$$, $$$R_1^A$$$, and $$$B_1$$$ are either known or measurable parameters. In this equation relative proton density of the two pools, $$$f$$$, and the exchange rate, $$$k_{ex}$$$, are the only two parameters to be determined. When using two saturation powers $$$B_{11}$$$ & $$$B_{12}$$$ to create two STRESS conditions, $$$f$$$ and $$$R_1^A$$$ can be canceled out and the exchange rate, $$$k_{ex}$$$, directly calculated from the following equation. $$k_{ex}^2=\frac{(γB_{11})^2×(γB_{12})^2×Mz,eq×(Mz,ss_1-Mz,ss_2)}{(γB_{12} )^2×Mz,ss_2×(Mz,eq-Mz,ss_1 )-(γB_{11} )^2×Mz,ss_1×(Mz,eq-Mz,ss_2))}{\phantom \cosin} (4)$$
Reaching two different steady states, theoretically requires long saturation durations, such as 10 s, which may induce unbearable SAR deposition in clinical applications. This problem can be overcome alternatively by noticing that 1) to calculate $$$k_{ex}$$$ from Eq.4 the only required parameters are the initial and final values of the magnetization for two $$$B_1$$$’s, and 2) the process of how the steady states are reached is not important, as eventually, it is an equilibrium when the two rates (saturation and T1 recovery) cancel each other. These enable one to induce the steady-states and to measure the exchange rate, in much shorter saturation times and negligible SAR deposition.
We developed a novel iSTRESS sequence as shown in Fig.2, in which an excitation RF pulse flips the magnetization by a small flip angle ($$$β$$$) followed by a short saturation pulse (ms to 0.5 s) to maintain a steady-state magnetization after the flip. To determine the saturation power ($$$B_{11}$$$ or $$$B_{12}$$$) for each iSTRESS condition, B1 is varied and the corresponding MR signals are measured to ensure that steady-state signal is maintained.
Method
We have programmed the novel iSTRESS sequence in a 9.4T preclinical MRI scanner (Agilent Technologies, Santa Clara, CA) and performed initial validation based on simulations and scanning of phantoms at varied pH. To validate the accuracy of the derived equation for calculating the exchange rate, we performed simulations with two-pool Bloch-McConnell equations and compared the determined kex from Eq.4 with the actual input kex. In vitro protein solution phantoms (20% w/w BSA in PBS, n=3) at varied pH (6.2, 6.6, 7.0 & 7.4) were scanned with iSTRESS protocol. The flip angles were β=10o & 20o. For each five Z-spectra were acquired, one right after the flip pulse and four with saturation duration= 0.5 s and saturation powers (B1=0, 25,50 & 100 Hz), and frequency offsets ranging from -6 to +6 ppm, +15.6 & +39.1 ppm. Mz at +2.75 ppm was used for the exchange rate analysis.Results
In the simulations, strong linear relationships with R2 = 0.999 were found between the input and calculated values as in Fig.3. In the phantom study, the calculated exchange rate showed an increase in kex with increasing pH (Fig.5), as expected [8].Discussion and conclusion
In this work, we proposed a novel method to induced saturation-transfer-recovery steady states for determining kex with low saturation power, short duration, and hence negligible SAR deposition. Our analytic approach was validated with simulations and imaging phantoms. The acquisition time for collecting the parameter was shortened from ~10s to ~2s. In conclusion, this study shows great promise for in vivo proton exchange rate imaging and its clinical applications.Acknowledgements
This work was supported by NIH grants R21EB023516, R01AG061114, and R21AG053876.References
[1] Zhou, J. et al. MRM 50: 1120-26. [2] Cai, K. et al. Nat. Med.18:302–306. [3] Shaghaghi, M. et al. QIMS.9:1686-96. [4] P. C. M. van Zijl, and N. N. Yadav, MRM 65: 927-948. [5] M. T. McMahon et al. MRM 55: 836-47. [6] Zhou, J. et al. MRM 51: 945-52. [7] K. Snoussi et al. MRM 49: 998-1005. [8] Jin T. et al. MRM 65:1448-60.Figures
Figure.1 Two
saturation transfer recovery steady-states (STRESS) with different Saturation
powers (B1’s)
Figure.2 A) An iSTRESS MRI pulse
sequence: an excitation RF pulse flips the magnetization by a small flip angle (β) followed by a saturation pulse and signal reading B)
The demonstration of two iSTRESS states under flip angles of 20o and
30o.
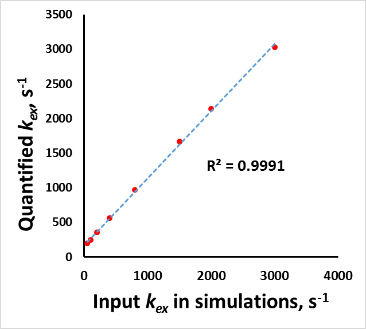
Figure.3 Simulations with Bloch-McConnell equations to compare
analytically derived proton exchange rates in Eq.4 with true values.
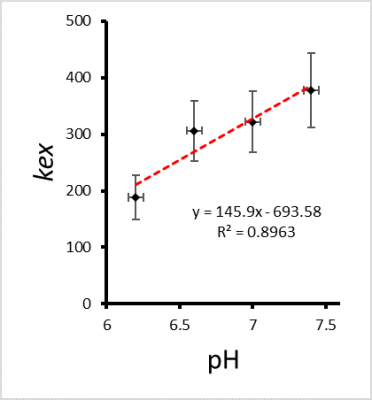
Figure.4 Phantom
study (BSA in PBS 20% (w/w) with 4 pH=6.2–7.4, n=3) indicates the exchange rate
increase with pH.