3017
The filtering effect of signal excitations on hyperpolarized imaging agents
James A Bankson1, Keith A Michel1, Zhan Xu1, Collin J Harlan1, Gary Martinez 1, and Christopher M Walker1
1Department of Imaging Physics, The University of Texas MD Anderson Cancer Center, Houston, TX, United States
1Department of Imaging Physics, The University of Texas MD Anderson Cancer Center, Houston, TX, United States
Synopsis
Imaging tumor metabolism using hyperpolarized (HP) pyruvate shows tremendous potential for new insight into disease and response to therapy, but these technically challenging measurements must be carefully designed to maximize accuracy and reproducibility. In this work, we explore the temporal filtering effects of signal excitations on observed HP MRI magnetization. The signal flow diagram and its associated transfer function confirm a low-pass filtering effect that can be controlled by the prescribed excitation angle and sampling interval. Low excitation angles promote temporal averaging but reduce sensitivity to higher frequency content. We explore the effects of signal excitation on quantification.
Introduction
Dissolution dynamic nuclear polarization can enhance signal from [1-13C]-pyruvate by more than four orders of magnitude (1), permitting unprecedented insight into metabolism in vivo. Upregulated aerobic glycolysis (the Warburg effect) is characteristic of many cancers, and can be visualized through the conversion of hyperpolarized (HP) pyruvate into lactate. A broad and growing range of literature indicates that metabolic MRI using HP pyruvate can inform on cancer aggressiveness and provide early indications of response to therapy (2). Our long-term goal is to establish metabolic MRI using hyperpolarized pyruvate as a quantitative imaging biomarker that can be used to guide care for patients with cancer. These measurements are technically challenging because the HP magnetization is finite, non-renewable, continually relaxing towards thermal equilibrium, and depleted with each signal excitation. Excitation strategies must be carefully designed because each excitation affects all future measurements. In this work, we seek to explore temporal filtering effects of signal excitations on observed HP MRI magnetization.Methods
The signal flow diagram for HP magnetization in tissue can be seen in Figure 1. In this hybrid discrete-continuous system, magnetization entering tissue is subjected to an excitation pulse, which controls the extent to which that magnetization is withdrawn for observation or allowed to remain and accumulate until the next excitation pulse. The transfer function for this system can be written as:$$H(z)=\frac{z\sin\alpha}{z-E_1\cos\alpha}$$
which reveals that the low-pass filter characteristics of this system can be controlled by the excitation angle ($$$\alpha$$$) and the sampling interval ($$$E_1=e^{-TR/T_1}$$$). The observable frequency content of signals that evolve within this system are modified by this low-pass filtering effect as illustrated in Figure 2.
HP MRI signal evolution is often characterized using the normalized ratio of HP lactate signal to total HP magnetization (nLac). Kinetic models can also be used to quantify the apparent rate at which HP pyruvate is converted into lactate ($$$k_{PL}$$$). To evaluate the filtering effects of signal excitation on nLac and $$$k_{PL}$$$, we generated synthetic data using a pharmacokinetic (PK) model of HP signal evolution that includes two physical compartments and two chemical pools (3,4) and was assumed to be driven by a pyruvate arterial input function that is consistent with our prior observations in vivo. nLac was calculated as the integral of HP lactate signal over time, normalized to the sum of the integrals for HP lactate and HP pyruvate. To minimize deconvolution of the filtering effect by using a PK model that perfectly corrects for relaxation and excitation losses, we fit dynamic data synthesized from the 2-compartment model ($$$k_{PL2}$$$) to a simpler precursor-product model with one physical compartment ($$$k_{PL1}$$$). Synthetic data was generated for constant excitation angles of 1-deg to 90-deg and a pan-physiological range of $$$k_{PL2}$$$ values. All simulations and analyses were carried out using Matlab (The Mathworks, Natick, MA). For clarity, we assume ideal excitation of a uniform volume.
Results
The low-pass filter profiles illustrated in Figure 2 show that temporal averaging using low excitation angles reduces sensitivity to more rapidly evolving HP magnetization, while higher excitations have more uniform sensitivity across the sampling bandwidth (1/TR). Differences in the frequency content of HP pyruvate and lactate signals which arrive via vasculature and chemical conversion, respectively, result in nLac (Figure 3) and $$$k_{PL}$$$ values (Figure 4) that are not independent of excitation angle. nLac, which is itself a temporally averaged measure, shows strong dependence on excitation angles (Figure 3) over physiologically reasonable values for $$$k_{PL2}$$$, and less contrast to high conversion rates or sampling with high excitation angles. Pharmacokinetic analyses using a simple precursor-product model (Figure 4) shows a more modest dependence on excitation angles, and that higher apparent rate constants are observed with the use of higher excitation angles: $$$k_{PL1,max}$$$ is observed at ~21-deg for $$$k_{PL2}$$$=0.01/sec and 0.1/sec, and 34-deg and 81-deg for $$$k_{PL2}$$$=1.0/sec and 10.0/sec, respectively.Discussion
This work explores the relationship between ideal HP MRI signal excitations and quantification methods that operate on magnetization that evolves within this system. Low excitation angles have a signal averaging effect that reduces sensitivity to rapid signal evolution that may be driven by delivery or chemical conversion, while higher excitation angles improve sensitivity to frequency content across the bandwidth defined by the sampling interval. Further study is needed to determine optimal acquisition conditions that maximize sensitivity to the expected frequency content of these signals, including effects of noise and the ability of PK models that account for this signal averaging effect to reduce bias imparted by excitations.Acknowledgements
This work was supported in part by the National Cancer Institute of the National Institutes of Health (R01CA211150) and GE Healthcare. The content is solely the responsibility of the authors and does not necessarily represent the official views of their sponsors.References
- Ardenkjaer-Larsen JH, Fridlund B, Gram A, Hansson G, Hansson L, Lerche MH, Servin R, Thaning M, Golman K. Increase in signal-to-noise ratio of > 10,000 times in liquid-state NMR. Proc Natl Acad Sci USA 100(18):10158-63, 2003.
- Kurhanewicz J, Vigneron DB, Ardenkjaer-Larsen JH, Bankson JA, Brindle K, Cunningham CH, Gallagher FA, Keshari KR, Kjaer A, Laustsen C, Mankoff DA, Merritt ME, Nelson SJ, Pauly JM, Lee P, Ronen S, Tyler DJ, Rajan SS, Spielman DM, Wald L, Zhang X, Malloy CR, Rizi R. Hyperpolarized (13)C MRI: Path to Clinical Translation in Oncology. Neoplasia 21(1):1-16, 2019.
- Bankson JA, Walker CM, Ramirez MS, Stefan W, Fuentes D, Merritt ME, Lee J, Sandulache VC, Chen Y, Phan L, Chou PC, Rao A, Yeung SC, Lee MH, Schellingerhout D, Conrad CA, Malloy C, Sherry AD, Lai SY, Hazle JD. Kinetic modeling and constrained reconstruction of hyperpolarized [1-13C]-pyruvate offers improved metabolic imaging of tumors. Cancer Res 75(22):4708-17, 2015.
- Walker CM, Fuentes D, Larson PEZ, Kundra V, Vigneron DB, Bankson JA. Effects of excitation angle strategy on quantitative analysis of hyperpolarized pyruvate. Magn Reson Med 81(6):3754-62, 2019.
Figures
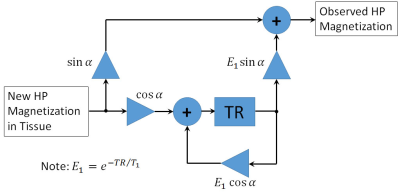
Figure 1.The signal flow diagram for HP magnetization in tissue. Signal that enters tissue is sampled by an $$$\alpha$$$-degree excitation pulse, which determines the fraction of magnetization that is removed for observation and that which remains to accumulate in tissue.
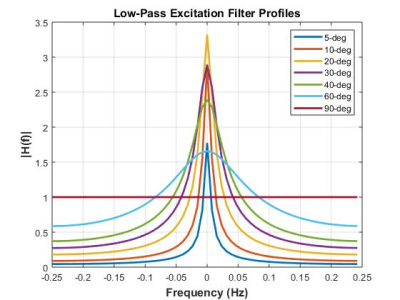
Figure 2. Low-pass filter profiles for the system illustrated in Fig.1, assuming TR=2s and T1=43s. Low excitation angles have a signal-averaging effect that reduces sensitivity to higher frequencies, while higher excitation angles show greater sensitivity to frequencies across the sampling bandwidth (1/TR).
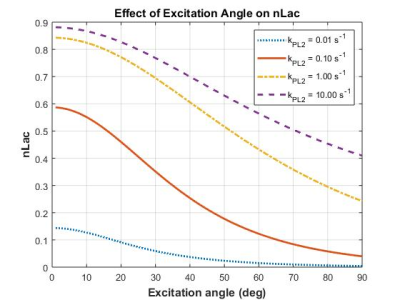
Figure 3. Effects of signal excitation on the normalized lactate ratio. Signal evolution was simulated using a 2-compartment model with kve=0.02s-1, vb=0.05, T1,Pyr=43s, T1,Lac=33s, with uniform excitations and apparent rate constant for chemical conversion (kPL2) as shown.

Figure 4. Effects of signal excitation on the first-order model of two-site exchange. Synthetic data was also fit to a simple precursor-product model to determine kPL1. PK modeling reduced bias imparted by excitations and showed improved dynamic range for assessing rapid evolution (kPL2≥1s-1) at higher excitation angles.