3016
Joint Image and Field Map Estimation for Multi-Echo Hyperpolarized 13C Metabolic Imaging
Julia Traechtler1, Valery Vishnevskiy1, Maximilian Fuetterer1, Andreas Dounas1, and Sebastian Kozerke1
1Institute for Biomedical Engineering, University and ETH Zurich, Zurich, Switzerland
1Institute for Biomedical Engineering, University and ETH Zurich, Zurich, Switzerland
Synopsis
An advanced signal model-based reconstruction jointly estimating image and field map from multi-echo, multi-coil acquisition of hyperpolarized metabolic data was developed and validated using synthetic and in-vivo data. Relative to standard multi-echo reconstruction methods, reconstruction accuracy improved by up to 30% for synthetic data considering realistic noise levels and field map gradients. Geometric distortion correction resulted in less than 20% error. For in-vivo data, the average improvement was 15%. Depending on the direction of the field gradients present, multi-coil reconstruction was found to be beneficial for addressing signal folding issues.
Introduction
Hyperpolarized 13C magnetic resonance imaging has shown potential for imaging metabolism of the in-vivo human heart1. Multi-echo acquisition2 combined with reconstruction techniques that deconvolve signal contributions of individual metabolites based on their known chemical shift3 have been proposed for hyperpolarized 13C MRI4. However, multi-echo reconstruction is sensitive to B0 induced phase offsets and therefore more advanced reconstruction techniques are required5,6. In the present work, a model-based reconstruction jointly estimating image and field map from multi-echo data is proposed and validated using synthetic and in-vivo data.Methods
An advanced model-based reconstruction of multi-echo, multi-coil hyperpolarized metabolic data is presented (cf. Fig-1). The signal model accounts for chemical shift $$$f(m)$$$ dependent spatial shifts of metabolite $$$m$$$ as well as distortions induced by varying in-plane off-resonances $$$B_0$$$. Sampling along a trajectory $$$\vec{k}$$$ at time points $$$t_s$$$ and considering weighting terms due to coil sensitivities $$$C(\vec{x})$$$ as well as $$$T_1$$$, $$$T_2^*$$$ relaxation, and spectral-spatial excitation $$$\alpha(\vec{x})$$$, yields the signal:$$\underbrace{s(\vec{k},d,e)}_{\vec{s}}=\underbrace{\sum_{\vec{x}}e^{j\vec{k}\vec{x}}\sum_m{}e^{j2\pi{}f(m)t(e)}\cdot{}C(\vec{x})\cdot{}e^{-\frac{t_{Dyn}(d)}{T_1(m)}}\cdot{}e^{-\frac{t(e)}{T^{*}_2(\vec{x},m)}}\cdot{}\sin\left(\alpha(\vec{x},m)\right)\cdot{}\cos\left(\alpha(\vec{x},m)\right)^{e-1}}_{\mathbf{E}}\cdot{}\underbrace{e^{j2\pi{}B_0(\vec{x})t(e)}}_{\mathbf{\hat{B}_0}}\cdot{}\underbrace{\rho(\vec{x},d,m)}_{\vec{\rho}}+\eta~~~\text{[1]}$$
where $$$t=t_s+TE$$$ with $$$TE$$$ being the echo time of echo $$$e$$$, $$$\rho$$$ denoting the spatiotemporal object of dynamic $$$d$$$ and $$$\eta$$$ Gaussian noise.
Rewriting equation [1] in matrix notation $$$\vec{s}=\left(\mathbf{E}\cdot{}\mathbf{\hat{B}_0}\right)\vec{\rho}$$$, allows to formulate image reconstruction as the following minimization problem optimizing jointly for image and B0:
$$\underset{\vec{\rho},\mathbf{\hat{B}_0}}{\text{argmin}}{}\left|\left|\left(\mathbf{E}\cdot{}\mathbf{\hat{B}_0}\right){}\vec{\rho}-\vec{s}\right|\right|_2^2+\lambda_{\rho}|\nabla_x\vec{\rho}|_1+\lambda_{\hat{B}_0}|\nabla_x\mathbf{\hat{B}_0}|_1$$
with $$$\lambda_{\rho}$$$, $$$\lambda_{\hat{B_0}}$$$ being regularization parameters and $$$|\cdot|_1$$$, $$$||\cdot||_2$$$ denoting the L1- and L2-norm, respectively.
The mathematical framework was implemented in Python using Tensorflow7 and executed on GPUs.
For the simulation study, echo-shift encoded data of metabolic signals were generated using the simulation framework as described previously8. An echo-planar imaging (EPI) trajectory (in-plane resolution=5x5mm2, FOV=85x85mm2) was used to generate synthetic k-space data for different high-resolution (1x1mm2) B0 maps and coil sensitivities. In-plane B0 maps with linear gradients, scaled by varying beta factors (relative phase encoding bandwidth), were used to examine geometric distortion and correction. Scaling by beta>0 stretches the object by a factor of (1+beta) and beta<0 results in object compression with beta=-1 being a projection of the object.
Image reconstruction and off-resonance estimation accuracies w.r.t. noise were analyzed for a single homogenous coil and constant beta=+0.2. The effects of multi-coil encoding were tested for aliasing (beta=+0.5) using simulated coil sensitivities generated using Biot-Savart’s law for one, two and four coils, respectively.
In-vivo applicability was evaluated on synthetic data using six coil sensitivity maps (estimated for reconstruction9) and three B0 map slices obtained from in-vivo data. Data was generated as the average of three sub-slices to account for through-slice B0 variations. Imaging parameters for the EPI trajectory were set according to in-vivo conditions: in-plane resolution=5x5mm2, FOV=220x220mm2, slice thickness=20mm, lactate signal-to-noise ratio (SNR) averaged over the myocardium of 15. Both EPI phase-encoding blip directions left/right were analyzed.
Finally, the proposed method was tested on in-vivo data acquired in three healthy pigs at 3T10 and compared to standard non-linear conjugate gradient-based reconstruction without B0 correction. Measured field maps (1H) served as reference for evaluating B0 estimation.
For the simulation studies, the pixel-wise normalized root-mean-square error (nRMSE) between reconstructed image and ground truth object were compared. For both, synthetic and in-vivo data, the DICE coefficient served as quantification metric for the reconstructed images. B0 estimation was evaluated based on the pixel-wise RMSE.
Regularization parameters were chosen according to RMSE using grid search.
Results
Fig-2 shows reconstructed images and estimated B0 maps for different in-plane B0 gradients beta=[+0.5,-0.5] corresponding to a maximum B0 range of 236Hz at the carbon resonance frequency at 3T. Reconstruction accuracy in terms of RMSE and DICE decreases linearly with increasing |beta| for reconstruction without B0 correction, whereas the proposed reconstruction shows improved accuracy for beta=[+0.2,-0.1]. In this range, distortion correction is feasible with less than 20% error.Fig-3 illustrates the reconstruction for a fixed B0 gradient as function of SNR and number of coils, respectively. For beta=+0.2, an increase in SNR to 12 significantly improves B0 estimation accuracy. In case of aliasing (beta=+0.5), increasing the number of coils from one to two/four improves image and B0 RMSE by 4%/5% and 14%/23%, and DICE by 2%/4%, respectively.
Fig-4 shows reconstruction results for data simulated with in-vivo B0 gradients for both EPI phase-encoding directions. For in-plane B0 gradients, the image RMSE of the proposed reconstruction is 14% lower compared to the standard reconstruction. Through-plane B0 gradients, which are not estimated, deteriorate reconstruction performance.
Fig-5 shows reconstructed in-vivo images with and without B0 correction. For all three examined in-vivo cases, the average improvement in DICE score accounts for 15% for the proposed method compared to standard reconstruction without B0 estimation.
Discussion
Advanced multi-echo, multi-coil reconstruction allows for joint estimation of image and field maps thereby addressing off-resonance induced geometrical distortions and resonance separation issues. Given the relatively low spatial resolution and SNR in hyperpolarized MRI, image and field map estimation were found to be limited by SNR and field gradients. Based on accepting 20% reconstruction error, a lactate SNR>=12 and a maximum field gradient covering 94Hz (beta=+0.2) is recommended. Depending on the direction of the field gradients, multi-coil reconstruction was shown to be beneficial in addressing signal folding issues.In conclusion, joint image and field map estimation holds promise to provide geometrically and chemically-shift consistent metabolic maps in multi-echo hyperpolarized MRI.
Acknowledgements
No acknowledgement found.References
- Cunningham CH, Lau JY, Chen AP, Geraghty BJ, Perks WJ, Roifman I, Wright GA, Connelly KA. Hyperpolarized 13C metabolic MRI of the human heart: initial experience. Circulation research. 2016 Nov 11;119(11):1177-82.
- Sigfridsson A, Weiss K, Wissmann L, Busch J, Krajewski M, Batel M, Batsios G, Ernst M, Kozerke S. Hybrid multiband excitation multiecho acquisition for hyperpolarized 13C spectroscopic imaging. Magnetic resonance in medicine. 2015 May;73(5):1713-7.
- Reeder SB, Pineda AR, Wen Z, Shimakawa A, Yu H, Brittain JH, Gold GE, Beaulieu CH, Pelc NJ. Iterative decomposition of water and fat with echo asymmetry and least‐squares estimation (IDEAL): application with fast spin‐echo imaging. Magnetic Resonance in Medicine: An Official Journal of the International Society for Magnetic Resonance in Medicine. 2005 Sep;54(3):636-44.
- Wiesinger F, Weidl E, Menzel MI, Janich MA, Khegai O, Glaser SJ, Haase A, Schwaiger M, Schulte RF. IDEAL spiral CSI for dynamic metabolic MR imaging of hyperpolarized [1‐13C] pyruvate. Magnetic resonance in medicine. 2012 Jul;68(1):8-16.
- Wiens CN, Friesen‐Waldner LJ, Wade TP, Sinclair KJ, McKenzie CA. Chemical shift encoded imaging of hyperpolarized 13C pyruvate. Magnetic resonance in medicine. 2015 Dec;74(6):1682-9.
- Busch J, Vishnevskiy V, Fuetterer M, Santelli C, von Deuster C, Peereboom S, Sauer M, Fleischmann T, Cesarovic N, Stoeck C, Kozerke S. Extended Signal Modelling and Regularization for Multi-Echo Hyperpolarized Metabolic Image Reconstruction. In: Proc. Intl. Soc. Mag. Reson. Med. 2018. p. 3568.
- Abadi M, Agarwal A, Barham P, et al.: TensorFlow: Large-Scale Machine Learning on Heterogeneous Distributed Systems. Softw available from tensorflow.org 2015.
- Traechtler J, Fuetterer M, Kozerke S. Limits of Kinetic Modeling for Myocardial Infarction and Border Zone Detection Using Hyperpolarized 13C Magnetic Resonance Imaging. In: Proc. Intl. Soc. Mag. Reson. Med. 2018. p. 4281.
- Uecker M, Ong F, Tamir JI, Bahri D, Virtue P, Cheng JY, Zhang T, Lustig M. Berkeley advanced reconstruction toolbox. InProc. Intl. Soc. Mag. Reson. Med 2015 May (Vol. 23, No. 2486).
- Fuetterer M, Traechtler J, Busch J, Dounas A, Peereboom S, Gastl M, Sauer M,
Fleischmann T, Cesarovic N, Stoeck C, Kozerke S. Longitudinal Hyperpolarized
13C Imaging of Metabolic Changes Following Myocardial Infarction in Pigs. In:
Proc. Intl. Soc. Mag. Reson. Med. 2019. p. 0721.
Figures
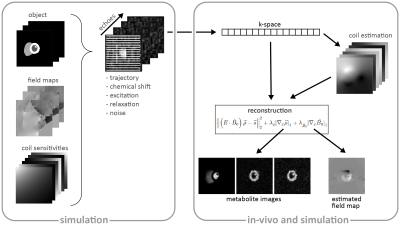
Fig-1 Reconstruction framework including the
interface to the simulation framework as previously proposed8. Prior
to reconstruction, coil sensitivity maps are estimated from the acquired
k-space9 and serve together with the multi-echo k-space data $$$\vec{s}$$$ as input for the proposed reconstruction which
optimizes jointly for image $$$\vec{\rho}$$$ and field map $$$B_0$$$. The encoding matrix $$$E$$$ accounts for chemical shift, relaxation,
excitation and the sampling trajectory.
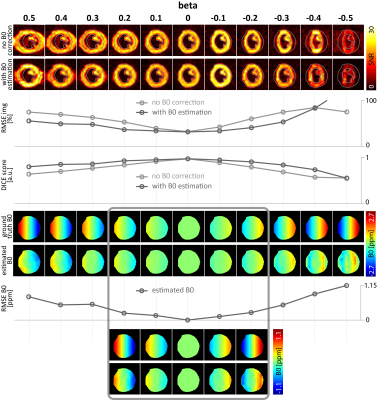
Fig-2 Reconstruction
performance of image and B0 estimation for different in-plane B0
gradients denoted by beta factors (relative to phase encoding bandwidth). B0
gradients in the range of beta=[+0.2,-0.1] can be estimated and corrected. For
|beta|>0.2, distortion correction performs better for stretching (beta>0)
than for compression (beta<0). For better visualization, B0 maps
are masked to the region of interest.
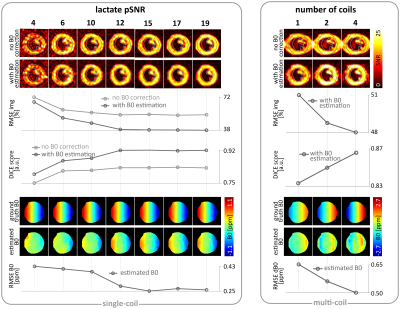
Fig-3 Reconstructed
images and estimated B0 maps for beta=+0.2 with varying lactate
pSNRs=[4,19] (left), and beta=+0.5 with varying number of coils (right). For a
linear B0 gradient of strength beta=+0.2, the required lactate pSNR
is 14 for less than 10% distortion error in terms of DICE score. For SNR>21,
image accuracy (RMSE) is not improved substantially with increasing
SNR values. Two and more coils improve the reconstruction accuracy in terms of
RMSE and DICE score for beta=+0.5.
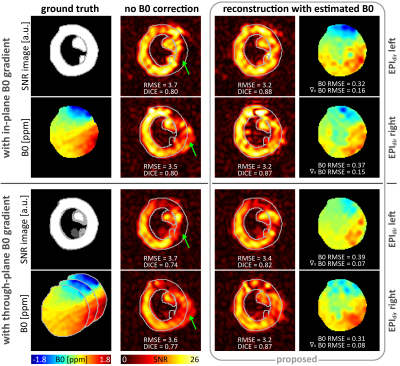
Fig-4 Reconstruction
for synthetic data with in- and through-plane B0 gradients. Reconstruction
accuracy in terms of RMSE and DICE is improved for the proposed method compared
to reconstruction without B0 estimation for both phase encoding blip
directions (EPIdir). Signal dephasing due to through-plane gradients
cannot be corrected. Visual assessment confirms better geometric alignment for
the proposed reconstruction. B0 estimation accuracy decreases in the
center due to missing signal in the left ventricle. For better visualization, images
are cropped and B0 maps masked.
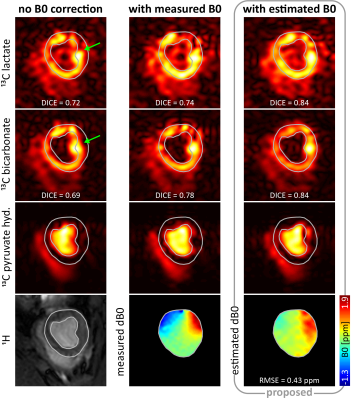
Fig-5 In-vivo images
of lactate, bicarbonate and pyruvate hydrate signals with and without B0
correction. Visual assessment and quantification by means of the DICE score
indicate improved results in terms of anatomical shape preservation w.r.t. the 1H-image
for the proposed reconstruction with B0 estimation. Especially in
the inferior and inferolateral myocardium (green arrow), reconstruction with B0
estimation compensates for myocardial distortions induced by off-resonances in
this region. For better visualization, images are cropped and B0 maps
masked.