2988

Comparison of low-rank denoising methods for accelerating the acquisition of ³¹P-MRSI

William T Clarke¹ and Mark Chiew¹
¹Wellcome Centre for Integrative Neuroimaging, NDCN, University of Oxford, Oxford, United Kingdom

Synopsis

Two new low-rank denoising methods are compared to an existing low-rank denoising method in ³¹P-MRSI data of human skeletal muscle and brain. All three methods increase the SNR of the noisy data above that of high SNR data acquired in 4-times the duration. Denoising algorithm parameters are examined using a grid search. Optimal algorithm choice is dataset dependent and incorrect selection of parameters can bias spectra.

Introduction

Phosphorous magnetic resonance spectroscopy (³¹P-MRS) is a low signal-to-noise ratio (SNR) technique due to the low ³¹P gyromagnetic ratio (40% of ¹H) and low concentrations of metabolites (1-10 mM). This necessitates long (>10 minute), low resolution (cm-scale) acquisitions. Long scan durations has limited the clinical applicability, despite promising diagnostic value (1).

The spectrum of ³¹P-visible metabolites is sparse, with <10 well-separated peaks visible in a ~25 ppm spectral range. Low-resolution acquisitions lead to smoothly varying spatial profiles. Denoising of ³¹P-MRS data is possible by exploiting the explicitly low-rank structure of the spectral-spatial data. One approach, low rank approximations (LORA)(2), has been applied to denoise basis spectra for further acquisition acceleration and in high resolution 9.4 T data (3,4).

Here we extend LORA in two ways. We combine two sub-steps of LORA into a single low-rank thresholding step. We also apply LORA in a patch-wise approach to exploit the locally lower-rank nature of the data, potentially capturing physiological variation. The proposed methods are applied in low SNR human skeletal muscle and brain data. The denoised data is compared to high SNR data from the same subjects.

Theory

All LORA-based denoising method exploits two distinct low-rank properties of a spatio-spectral dataset: (i) partial separability of spatio-temporal modes due to correlated spectral information across space, and (ii) linear predictability of each voxel time-course due to the sparse spectral composition.

The original LORA method enforces low-rank constraints for denoising serially in two steps, first, truncating the SVD of the space-time Casorati matrix formed by the data, then voxel-wise by constraining the rank of a Hankel matrix formed by sliding a window across the voxel time-course. This requires 2 threshold parameters, R1 and R2.

The tLORA variant forms a tensor, such that the frontal slices of the tensor correspond to the Hankel matrices for each voxel. Then, a single low-rank threshold is applied to the tensor unfolding that corresponds to a vertical concatenation of the voxel-wise Hankel matrices, simultaneously enforcing both low-rank constraints with a single parameter R1.

The lLORA variant operates in a patch-wise manner, employing an operator P to extract spatial patches of the dataset with some geometry parameters (size and overlap). Then, standard LORA is performed on each patch, where R1 is typically reduced to reflect the smaller patch spatial dimensionality. Finally, the pseudoinverse patch operator P is applied to the set of patches to reconstruct the dataset.

Methods

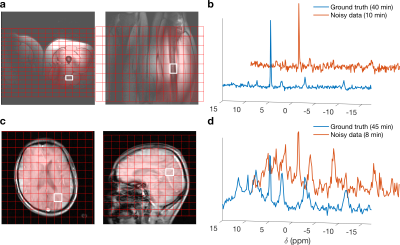
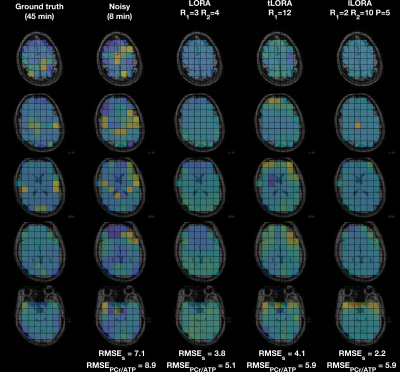
LORA, tLORA and lLORA were applied to two datasets, using a grid search to examine the effect of rank parameters (all methods) and patch size (lLORA). The first dataset (Fig 1c&d) was acquired from a human brain at 3T (Siemens Trio) equipped with a ¹H/³¹P-birdcage coil (Rapid Biomedical, Germany). Data was acquired using an acquisition-weighted CSI sequence (5). 230x230x200 mm³ FoV, 12x12x12 matrix, 4 kHz bandwidth, 512 samples, 1s T_R, 40° flip-angle (uniform across 6 to −16 ppm). Noisy data had a single average at the centre of k-space (T_A=8:37 min), “ground truth” data had 22 averages (T_A=44:23 min).

The second dataset (Fig 1a&b) was acquired from a human thigh at 7T (Siemens Magnetom) using a quadrature surface coil using the same acquisition-weighted CSI. 220x350x240 mm³ FoV, 16x16x8 matrix, 6 kHz bandwidth, 512 samples, 1s T_R, uniform excitation from 6 to −16 ppm. Noisy data was acquired with a single average (T_A=10:05 min), “ground truth” data was acquired with 16 averages in (T_A=40:13 min).

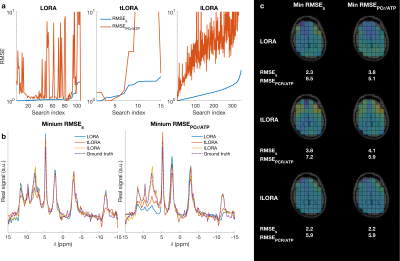
Data was fitted in the OXSA toolbox (6), coil data was combined after denoising using WSVD (7). Denoised data was compared to ground truth using two metrics in voxels selected using ¹H localiser images:$$RMSE_S=\left\|\rho_{noisy}(\nu)-\rho_{GT}(\nu)\right\|$$
$$RMSE_{PCr/ATP}=\left\|PCr/ATP_{noisy}-PCr/ATP_{GT}\right\|$$Where $$$\rho(\nu)$$$ is the spectra in the masked voxels and $$$PCr/ATP$$$ is the metabolite ratio in each voxel.

Results

All methods significantly denoised the spectra (Fig 2). Mean matched-filter PCr SNR was 31-times higher in the LORA denoised data than the noisy dataset in the brain, exceeding the SNR of the “ground truth” datasets.

In the brain, the evaluation metrics were not simultaneously minimised for LORA and tLORA but were for lLORA (Fig 3a). Spectra (Fig 3b) and PCr/ATP maps (Fig 3c) show optimal parameter sets for the two different metrics in LORA and tLORA produce different spatial distributions and spectral profiles (especially >5 ppm). The joint minimum lLORA parameter set has good spatial and spectral fidelity to ground truth data (Fig 4).

In the skeletal muscle (Fig 5) tLORA results in the lowest RMSE_S and RMSE_PCr/ATP but RMSE_PCr/ATP performance of lLORA is below that of noisy data.

Discussion

The examined methods could be a powerful way of recovering high quality data from noisy ³¹P-MRS data collected in short, clinically acceptable timeframes. tLORA benefits from having fewer input parameters than LORA, whereas lLORA may be more robust to spatial heterogeneity. In separate cases, tLORA and lLORA have outperformed LORA. However, selection of the right algorithm and parameter set is essential to not bias results. It is essential that proper validation is carried out on these methods before use.
LORA has been modified to work across compartments (CLORA)(8), which we have not assessed. tLORA and lLORA could be combined with CLORA or extended further to exploit multiple receive coils.

Acknowledgements

The Wellcome Centre for Integrative Neuroimaging is supported by core funding from the Wellcome Trust (203139/Z/16/Z). MC is supported by the Royal Academy of Engineering (RF201617\16\23).

References

1. Neubauer S. Mechanisms of disease - The failing heart - An engine out of fuel. New Engl J Med 2007;356(11):1140-1151.

2. Nguyen HM, Peng X, Do MN, Liang ZP. Denoising MR spectroscopic imaging data with low-rank approximations. IEEE Trans Biomed Eng 2013;60(1):78-89.

3. Ma C, Clifford B, Liu Y, Gu Y, Lam F, Yu X, Liang ZP. High-resolution dynamic (31) P-MRSI using a low-rank tensor model. Magn Reson Med 2017;78(2):419-428.

4. Ruhm L, Dorst J, Avdievich N, Wright A, Mirkes C, Bause J, Scheffler K, Henning A. 31P MRSI of the human brain at 9.4 T: Metabolic imaging applying low-rank denoising. 2019; Proc. Intl. Soc. Mag. Reson. Med. 27, Montreal. p 2477.

5. Rodgers CT, Clarke WT, Snyder C, Vaughan JT, Neubauer S, Robson MD. Human cardiac 31P magnetic resonance spectroscopy at 7 Tesla. Magn Reson Med 2014;72(2):304-315.

6. Purvis LAB, Clarke WT, Biasiolli L, Valkovic L, Robson MD, Rodgers CT. OXSA: An open-source magnetic resonance spectroscopy analysis toolbox in MATLAB. PLoS One 2017;12(9):e0185356.

7. Rodgers CT, Robson MD. Receive array magnetic resonance spectroscopy: Whitened singular value decomposition (WSVD) gives optimal Bayesian solution. Magn Reson Med 2010;63(4):881-891.

8. Liu Y, Ma C, Clifford BA, Lam F, Johnson CL, Liang ZP. Improved Low-Rank Filtering of Magnetic Resonance Spectroscopic Imaging Data Corrupted by Noise and B(0) Field Inhomogeneity. IEEE Trans Biomed Eng 2016;63(4):841-849.

Figures

Figure 1. In vivo datasets. a&c CSI grid overlaid on ¹H localisers. Evaluation metrics were calculated in the masked tissue regions shown here as red highlighted voxels. b&d Example muscle and brain spectra from noisy and “ground truth” datasets from the white-outlined voxel shown in a & c. Spectra shown are apodised by 15 Hz.

Figure 2. Denoised spectra from each method (black) and the difference to the ground truth (grey) in the voxel outlined in Fig 1a&c. LORA parameters are selected for minimum RMSE_PCr/ATP. Difference to ground truth is shown increased by a factor of 5 (skeletal muscle) and 2 (brain). Spectra are shown apodised by 30 Hz (skeletal muscle) and 15 Hz (brain).

Figure 3. Selection of LORA parameters. a RMSE_S and RMSE_PCr/ATP for all evaluated parameter sets for each method for the brain dataset shown on a log scale. lLORA achieved a joint minimum. b Spectra for each denoising method for minimum RMSE_S and RMSE_PCr/ATP. Selecting using RMSE_PCr/ATP results in distorted peaks above 5 ppm for LORA and tLORA. c Spatial maps of PCr/ATP in a single slice for all three methods with parameter sets selected for minimum RMSE_S and RMSE_PCr/ATP. LORA appears to show low ratio values in regions of high B₀ offset.

Figure 4. Spatial maps of PCr/ATP in the brain for ground truth and noisy datasets and for all three denoising methods. Parameters have been chosen to minimise RMSE_PCr/ATP. The maps are overlaid on axial ¹H localiser images.

Figure 5. Spatial maps of PCr/ATP in skeletal muscle for ground truth and noisy datasets and for all three denoising methods. Parameters have been chosen to minimise RMSE_PCr/ATP. The maps are overlaid on axial ¹H localiser images.

Proc. Intl. Soc. Mag. Reson. Med. 28 (2020)

2988