Introduction

Dynamic deuterium MR spectroscopic imaging (²H-MRSI) is emerging as a powerful tool for monitoring the metabolic activities with the administration of deuterated substrates.^1-3 However, its practical utility is limited by poor signal-to-noise ratio (SNR) due to its inherently low detection sensitivity and molecular concentrations. In this work, we propose a novel method to reconstruct the desired spatiospectral distributions from noisy dynamic ²H-MRSI data with high spatiotemporal resolution, incorporating a physics-based subspace spectral model and deep learning-based data priors via an information-theoretical framework. Both simulation and experimental results show that the proposed method significantly outperforms the conventional reconstruction method.

Method

In the Fourier imaging framework, the measured dynamic ²H-MRSI data can be expressed as:
$$\hspace{16em}d(\boldsymbol{k},t,T)=\iint\rho(\boldsymbol{x},f,T)e^{-i2\pi\boldsymbol{k}\boldsymbol{x}}e^{-i2{\pi}ft}d\boldsymbol{x}df+\xi(\boldsymbol{k},t,T),\hspace{16em}(1)$$
where $$$\rho(\boldsymbol{x},f,T)$$$ represents the desired image function and $$$\xi(\boldsymbol{k},t,T)$$$ the Gaussian noise. The conventional method represents $$$\rho(\boldsymbol{x},f,T)$$$ in terms of a truncated Fourier series, which has many degrees-of-freedom (DOF). The reconstruction thus obtained often has large estimation uncertainty in the presence of large measurement noise $$$\xi(\boldsymbol{k},t,T)$$$ as is often the case with ²H-MRSI experiments.

Union-of-subspaces spectral model
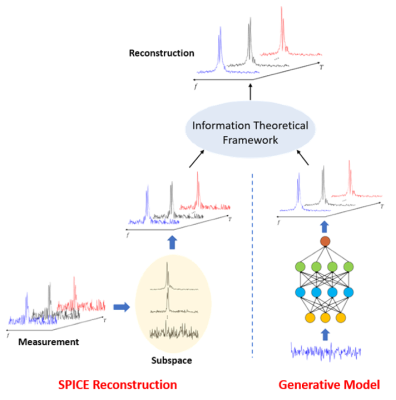
To overcome the shortcomings of the Fourier model, we use a physics-based union-of-subspaces model to represent the desired spatiospectral function, which was first introduced in SPICE for fast MRSI^4-6:
$$\hspace{20.5em}\hat{\rho}(\boldsymbol{x},f,T)=\sum_{\ell=1}^{L}\sum_{q=1}^{Q_{\ell}}a_{q,\ell}(\boldsymbol{x},T)\varphi_{q,\ell}(f).\hspace{20.5em}(2)$$
This subspace model significantly reduces the DOF and also enables efficient incorporation of available spectral priors obtained by pre-learning the spectral basis functions $$$\{\varphi_{q,\ell}(f)\}$$$ from high-SNR training datasets.

Deep-learning data priors
To further enhance our capability to handle large measurement noise, we incorporate prior distributions of ²H-MRSI data. Such distributions are learned from training data with high SNR. In order to learn these prior distributions effectively, we build a generative model for each molecule using DCGAN (deep convolutional generative adversarial networks).⁷ After being trained properly, the generator generates spectral-temporal functions for each molecule (e.g., glucose, water, ….) according to prior distributions embedded in the training data.

Integration of subspace model and generative model
We use an information-theoretical framework to synergistically integrate the physics-based spectral model with the data-driven priors. More specifically, we first obtain a subspace model-based reconstruction by solving the following optimization problem:
$$\hspace{16.8em}\{\hat{a}_{q,\ell}\}=\arg\min_{\{a_{q,\ell}\}}\left\vert\left\vert{d}(\boldsymbol{k},t,T)-\mathcal{F}\left(\sum_{\ell=1}^{L}\sum_{q=1}^{Q_{\ell}}a_{q,\ell}(\boldsymbol{x},T)\varphi_{q,\ell}(f)\right)\right\vert\right\vert_2^2,\hspace{16.8em}(3)$$
where $$$\mathcal{F}(\cdot)$$$ denotes the 2D Fourier operator along $$$(\boldsymbol{x},f)$$$. We then synthesize an initial estimate as $$$\tilde{\rho}(\boldsymbol{x},f,T)=\sum_{\ell=1}^{L}\sum_{q=1}^{Q_{\ell}}\hat{a}_{q,\ell}(\boldsymbol{x},T)\varphi_{q,\ell}(f)$$$. To incorporate the data-driven priors, we solve the following constrained optimization problem voxel-by-voxel (ignoring $$$\boldsymbol{x}$$$):
$$\hspace{19em}\min_{\rho(f,T),\rho_{g}(f,T)\sim{P}_{\mathcal{g}}}\iint\rho(f,T)\log\frac{\rho(f,T)}{\rho_g(f,T)}dfdT\hspace{19em}$$
$$\hspace{24.3em}\text{subj.}\:\text{to}\:\tilde{\rho}=\mathcal{F}(\rho),\hspace{24.3em}(4)$$
where $$$\rho_g(f,T)$$$ represents samples drawn from the pre-trained generative model. The above formulation is motivated by the minimum cross-entropy principle which forces the solution to be similar to the generated sample plus any new spectral and temporal features strongly supported by the experimental data.^8,9 It can be proved that the optimal solution to Eq. (4) takes the form as⁸:
$$\hspace{18em}\rho(f,T)=\rho_g(f,T)\sum_{n}\sum_{n'}c_{nn'}e^{i2\pi{n}\Delta{t}f}e^{i2\pi{n'}\Delta{F}T},\hspace{18em}(5)$$
where $$$\Delta{t}$$$ is the sampling rate of the FID signals, $$$\Delta{F}$$$ the spectral resolution corresponding to $$$T$$$. In practice, since the probability density function $$${P}_{\mathcal{g}}$$$ is often intractable, we actively generate “feasible” samples $$$\rho_{g}(f,T)\sim{P}_{\mathcal{g}}$$$ and solve Eq. (4) (via Eq. (5)) until the cross-entropy between $$$\rho(f,T)$$$ and $$$\rho_g(f,T)$$$ is lower than some preset threshold.
Figure 1 illustrates the key elements of the proposed method for dynamic ²H-MRSI reconstruction.

Results

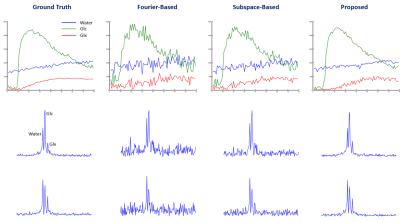
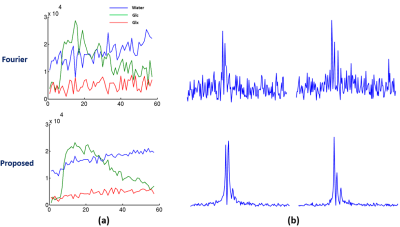
In vivo data were collected from Sprague Dawley rats on a 16.4 T scanner (Varian/VNMRJ) with both passively decoupled ²H and ¹H surface coils. The rats were anesthetized by 2% isoflurane and infused (i.v.) with deuterated glucose before the experiments. All data were acquired using the 3D-CSI sequence with TR = 45 ms and FOV = 2.8×2.8×2.4 cm³. For training data, we collected $$$9×9×5$$$ phase encodings with 80 dynamic volumes (69 sec/volume). For high-resolution but low-SNR data, we acquired 17×17×5 phase encodings with 60 dynamic volumes (105 sec/volume). The training data were interpolated to match the volume rate of the high-resolution data during post-processing.
We have evaluated the performance of the proposed method using both simulated and in vivo data. In the simulation study, the dataset was generated using realistic spectral parameters with additive Gaussian noise. We compared the proposed method to the Fourier-based and subspace-based methods. As shown in Fig. 2 and Fig. 3, the proposed method significantly reduced the signal fluctuations of key molecules (Glc: glucose, Glx: glutamate + glutamine; and water) along both temporal and spatial dimensions and produced much more accurate results. We have also tested our method using in vivo data obtained from a rat brain using high-resolution acquisition. As shown in Figs. 4 and 5, the proposed method significantly outperformed over the conventional methods, which was consistent to the simulation study.

Conclusions

This work proposes a novel method for reconstructing dynamic ²H-MRSI data, which synergistically integrates a physics-based subspace spectral model with data-driven priors obtained from training data using deep learning. Both simulation and in vivo experimental studies show that the proposed method yields significantly improved reconstruction results. The advancement allows us to achieve high spatial and temporal imaging resolution with high fidelity, which is critical for performing kinetic modeling and quantification of energy metabolism. This method is expected to be useful for many applications involving dynamic ²H-MRSI, in particular, valuable for imaging the Warburg effect in tumors.

Acknowledgements

This work reported in this paper was supported, in part, by the following research grants: R21EB023413, R01CA240953, R01MH111413, U01EB026978, P41EB027061, P30NS076408 and S10RR025031.