Introduction

J-resolved (or Multi-TE) MRSI encodes the J-coupling of different molecules and allows for improved spectral separation and quantification^1-3. However, the need of acquiring data at multiple TEs leads to multiplied acquisition time, thus further limiting the trade-offs among SNR, speed and spatiospectral resolution. Although fast-scanning methods such as EPSI-based sequences can be used for acceleration, low-resolution data is typically acquired in practice to maintain a reasonable scanning time and SNR^3-5. The increased voxel size makes the experiments more susceptible to B₀ inhomogeneity, leading to undesirable lineshape distortions and SNR loss. The conjugate phase (CP) method⁴ can correct the B₀-induced frequency shifts by performing reconstruction at higher-resolution grids than the acquired data to improve lineshapes. But its performance is often limited due to the inherent ill-posedness of the reconstruction problem. An overdiscrete reconstruction has been introduced to optimize the voxel spatial response functions thus minimizing the B₀ effects⁶. Constrained reconstruction has been recently proposed as an alternative approach to address the ill-posed B₀ correction problem^7-9 for single-TE acquisitions while they can be applied to J-resolved MRSI by treating each TE independently, the performance degrades as TE increases (lower SNRs) and they do not effectively exploit the correlation in the multi-TE data. We proposed here a new method to reconstruct low-resolution J-resolved MRSI data with B₀ correction, using joint multi-TE low-rank and spatial constraints. Simulation and in vivo studies have been conducted to evaluate the proposed method.

Method

The data acquired in a J-resolved MRSI experiment can be expressed as:$$d(\mathbf{k},t_2,t_1)=\int \rho(\mathbf{r},t_2,t_1)e^{-i2\pi\Delta f(\mathbf{r})t_2}e^{-i2\pi\mathbf{kr}}d\mathbf{r}+n(\mathbf{k},t_2,t_1), \quad\quad\quad(1)$$ where $$$\rho(\mathbf{r},t_2,t_1)$$$ denotes the desired multi-TE spatiotemporal function, with $$$t_2$$$ the chemical shift encoding time (FID) and $$$t_1$$$ the J-coupling encoding time (TE), $$$d(\mathbf{k},t_2,t_1)$$$ denotes the acquired $$$(k,t)$$$-space data, $$$\Delta f(\mathbf{r})$$$ B₀ inhomogeneity maps and $$$n(\mathbf{k},t_2,t_1)$$$ the noise. After discretization, Eq. (1) can be written in the following matrix representation:$$\mathbf{d_{t_1}}=\Omega\{\mathbf{FB}\odot\boldsymbol{\rho}_{t_1}\} + \mathbf{n_{t_1}}, \quad\quad\quad(2)$$where $$$\boldsymbol{\rho}_{t_1}$$$ is a Castrati matrix of the spatiotemporal function at each TE⁹, $$$\mathbf{B_{nm}}=e^{i2\pi\mathbf{r_n}t_{2,m}}$$$ (B₀-induced linear phase), $$$\mathbf{F}$$$ the Fourier transform matrix with $$$\Omega$$$ a $$$k$$$-space truncation operator and $$$\mathbf{n}$$$ is the noise vector. Because the model in Eq. (2) is only accurate when the B₀ inhomogeneity is almost constant within each voxel, $$$\boldsymbol{\rho}_{t_1}$$$ needs to be modeled on higher-resolution grids than that afforded by $$$\mathbf{d}_{t_1}$$$ to ensure sufficiently small voxel sizes, making the problem ill-posed.
We describe here a constrained reconstruction method to address this challenge for multi-TE MRSI. Specifically, we model $$$\boldsymbol{\rho}_{t_1}$$$ using a long Casorati matrix $$$\boldsymbol{\rho}=[\boldsymbol{\rho}_{_{TE_1}},\boldsymbol{\rho}_{_{TE_2}},...,\boldsymbol{\rho}_{_{TE_N}}]$$$, where $$$\boldsymbol{\rho}_{_{TE_i}}$$$ denotes the matrix of the $$$i$$$-th TE. Inspired by the subspace model of $$$\boldsymbol{\rho}_{\mathbf{r},{t_2}}$$$ described in (10-11) and the resulting low-rank property of $$$\boldsymbol{\rho}_{_{TE_i}}$$$ (for a single $$$t_1$$$), we model $$$\boldsymbol{\rho}$$$ using an explicit low-rank decomposition: $$\boldsymbol{\rho}=\mathbf{UV}=\mathbf{U}[\mathbf{V}_{_{TE_1}},\mathbf{V}_{_{TE_2}},...,\mathbf{V}_{_{TE_N}}],\quad\quad\quad(3)$$ which indicates each $$$\boldsymbol{\rho}_{_{TE_i}}$$$ can be modeled as $$$\boldsymbol{\rho}_{_{TE_i}}=\mathbf{UV}_{_{TE_i}}$$$. Furthermore, we exploit a high-resolution anatomical image readily available in an MRSI experiment to derive prior spatial edge information to constrain the spatial variations in multi-TE spatiotemporal function of interest. Integrating these two constriants, we formulate the reconstruction as: $$\{\hat{\mathbf{U}},\hat{\mathbf{V}}\}=\arg\min_{\mathbf{U},\mathbf{V}}\|\mathbf{d}-F_{\Omega}\{\mathbf{B}\odot\mathbf{UV}\}\|^2_2+\lambda_1\|\mathbf{WDUV}\|^2_F,\quad\quad\quad(4)$$ where $$$\mathbf{d}$$$ is a vector containing the low-resolution data at all TEs, $$$F_{\Omega}$$$ the Fourier encoding operator with $$$k$$$ space truncation $$$\Omega$$$, $$$\mathbf{B}$$$ models B₀ inhomogeneous effect (a concatenation of B matrices for different TEs). $$$\odot$$$ a point-wise multiplication operator, $$$\mathbf{W}$$$ contains the edge weights derived from anatomical images, and $$$\mathbf{D}$$$ is a finite difference operator. $$$\lambda_1$$$ is the parameter for a mild weighted-$$$\ell_2$$$ regularization. We solve this optimization problem by alternatively minimizing it w.r.t $$$\mathbf{U}$$$ and $$$\mathbf{V}$$$. Initial guesses of $$$\mathbf{U}$$$ and $$$\mathbf{V}$$$ are obtained by performing an SVD to a minimum-norm reconstruction. The rank was selected empirically by observing the singular value decay.

Results and Discussion

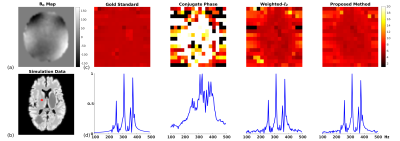
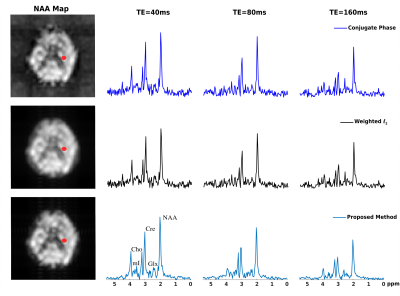
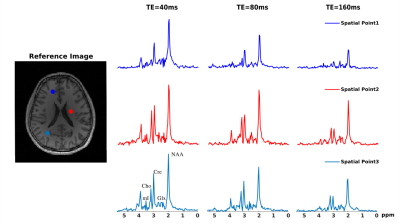
A computational J-resolved MRSI phantom (64×64voxels at 3 TEs) was simulated to validate the proposed method. The phantom contains spatially varying spectra of different molecules generated using GAVA¹² and further combined with different ratios according to segmented regions(Fig. 1b). A high-resolution experimentally acquired B₀ map was used to introduce the B₀ effects (Fig. 1a). Noise was added at various peak SNR levels. Figures 1 and 2 compare the B₀ corrected reconstruction from 16×16 k-space data by different methods, i.e., CP method, a weighted-$$$\ell_2$$$ method and the proposed method. As can be seen, the proposed method corrected B₀-induced lineshape distortion better than alternative methods (Fig. 1) as well as offer extra SNR gains across all TEs (Fig. 2). In vivo data were acquired from healthy volunteers on a Siemens 3T scanner (Prisma) using a customized 3D J-resolved spin-echo EPSI sequence .The acquisition parameters are: FOV=220×220×64mm³, matrix size=24(k_x)×20(k_y)×8(k_z), TR=1300ms, 3 TEs at 40, 80, 160ms, spectral BW=1200Hz and 256 gradient echoes for each TE. Results were compared for the CP reconstruction, weighted-$$$\ell_2$$$ regularized reconstruction and the proposed method (Figs. 3-4). Again, the proposed method produced B₀-corrected reconstruction with the best spectral quality and SNR.

Conclusion

We have developed a new method for B₀ inhomogeneity corrected reconstruction from low-resolution J-resolved MRSI acquisitions. The proposed method jointly reconstruct the data at multiple TEs and solves this ill-posed problem using joint low-rank and spatial edge constraints. Both simulation and in vivo results demonstrated improved lineshape and SNR achieved by the proposed method over existing methods applied to individual TEs.

Acknowledgements

No acknowledgement found.