2874
Development of absolute quantitation method in 1H MRS at high magnetic field
Hidehiro Watanabe1, Nobuhiro Takaya1, and Fumiyuki Mitsumori1
1Center for Environmental Measurement and Analysis, National Institute for Environmental Studies, Tsukuba, Ibaraki, Japan
1Center for Environmental Measurement and Analysis, National Institute for Environmental Studies, Tsukuba, Ibaraki, Japan
Synopsis
The method for absolute quantitation of 1H MRS in a human brain at high B0 field was proposed. A water phantom as a concentration reference and a human brain area measured separately. The ratio of the reception sensitivities between uniform areas in the phantom and in the human brain can be computed from measured B1+s. The ratio between the VOI and the uniform area in the human brain can be computed by our previously reported ratio map method. Then, concentration in the VOI can be calculated. Our method was demonstrated in the phantom experiments.
Introduction
High field 1H MR spectroscopy in human brain has advantages in high sensitivity and spectral resolution. This feature can lead to accurate quantitation. In absolute quantitation of metabolites of human brains in 1H MRS, tissue water is widely used as an internal concentration reference [1]. Water content in a volume of interest (VOI) is estimated from fractions of GM, WM and CSF with the literature values. However, pathological changes of water content will cause quantitation error. This problem can be resolved using an external concentration reference (Fig. 1). However, this method cannot be used at high B0 field due to B1 inhomogeneity.One of important findings on B1 that the transmission RF field and the reception sensitivity are represented as B1+ and B1-, respectively and that these fields differ in spatial distribution at high B0 field even when a transceiver RF coil is used [2]. While B1+ can be measured, reception sensitivity of B1- cannot be measured in human brains because it is always associated with signal intensities. Then, reception sensitivities between the VOI in a human brain and the external reference cannot be compared at high B0 field.
We have reported that the linear relationship exists between B1+ and B1- around a uniform area even at high B0 field [3]. Water content maps could be measured in human brains using this relationship at 4.7T. In this work, we will apply this relationship to absolute quantitation in 1H MRS at high B0 field and will demonstrate measurement of concentration in experiments using water phantoms.
Methods
Proposed absolute quantitation methodIn our proposed method, a water phantom as a reference and a human brain are measured separately (Fig. 2). The following measurements are required to obtain a reception sensitivity in the VOI of a human brain; B1+ maps both in the phantom and in the human brain, and localized water signal in a uniform area in the phantom. Form the finding that the linear relationship exists between B1+ and B1- around a uniform area [3], the ratio of reception sensitivities of B1-s in uniform areas (red squares in Fig. 2), denoted as Coefuniform can be expressed by the ratio of measured B1+s.
$$\begin{align}Coef_{uniform}&=\frac{B_{1\ \ brain.uniform}^{-}}{B_{1\ \ ref.uniform}^{-}}\\&=\frac{B_{1\ \ brain.uniform}^{+}}{B_{1\ \ ref.uniform}^{+}}\tag{1}\end{align}$$
where subscript texts of brain.uniform and ref.uniform denote the uniform area inside the human brain and that inside the reference phantom, respectively. Next, B1-s can be compared between the VOI (yellow dotted square) and the uniform area (red dotted square) in the human brain using our previously reported ratio map method [4].
$$Coef_{VOI}=\frac{B_{1\ \ brain.VOI}^{-}}{B_{1\ \ brain.uniform}^{-}}.\tag{2}$$
From these equations, reception sensitivities can be compared between the VOI in the human brain and the uniform area (red square) in the reference phantom.
$$\begin{align}Coef&=Coef_{VOI}\times Coef_{uniform}\\&=\frac{B_{1\ \ brain.VOI}^{-}}{B_{1\ \ ref.uniform}^{-}}.\tag{3}\end{align}$$
Then, concentration of a metabolite in the human brain denoted as Concmetab can be computed by
$$Conc_{metab}=Conc_{ref}\times \frac{PA_{brain.VOI.metab}}{Coef\times PA_{ref.uniform}}\tag{4}$$
where Concref and PAref.uniform denote the concentration of water that is 55.5 M and a peak area of water in the uniform area in the phantom, respectively, and PAbrain.VOI.metab denotes PA of a metabolite in the localized 1H spectrum of the human brain.
Experiments
All experiments were performed using a 4.7T whole-body MR system (INOVA, Agilent) by using a volume TEM coil both for transmission and reception. To demonstrate the proposed absolute quantitation method, we performed experiments with a cylinder water phantom with 150-mm diameter and 170-mm length as a reference (Fig. 3a) and a spherical saline phantom with 130-mm diameter for measuring (Fig. 3b). Absolute B1+ maps were measured by the phase method where a set of two SE images were acquired using hyperbolic secant pulses form both excitation and refocusing [5]. The same conditions of RF power were used both in the phantom and in the human brain. Instead of the ratio map in a human brain, a reception sensitivity map in the saline phantom for measuring was measured by an adiabatic SE sequence [6] to avoid B1+ inhomogeneity with condition of TR/TE = 4000/26 ms. Localized water signals both in the uniform area (red square in Fig. 3a) in the reference phantom and in the VOI (yellow dotted square) in the saline phantom were measured by the STEAM sequence with TR/TE = 15,000/4 ms. The VOI was set up around the edge of the phantom of non-uniform area (Fig. 3b). The voxel volumes were 8ml in the both phantoms.
Results & Discussion
Amplitudes of B1+ in the uniform areas are 0.234 [KHz] in the reference phantom and 0.123 [KHz] in the saline phantom for measuring, respectively. The ratio of the VOI to the uniform area calculated from measured B1- map in the saline phantom was 0.776 (Fig. 3). The peak areas of the water spectra in arbitrary units were 141.8 in the reference phantom and 56.5 in the saline phantom, respectively. Then, a concentration of water in the saline phantom for measuring was calculated as 54.2 [M] using Eq. 4 whose error was -2.3% to 55.5 [M].Conclusions
Our proposed method is useful for absolute quantitation in 1H MRS at high B0 field. This can also be applied in a human brain.Acknowledgements
No acknowledgement found.References
- Barker PB., Soher BJ., Blackband SJ., Chatham JC., Mathews VP., Bryan RN., Quantitation of proton NMR spectra of the human brain using tissue water as an internal concentration reference. NMR Biomed. 1993;6:89-94.
- Hoult DI., The principle of reciprocity in signal strength calculations – a mathematical guide. Concepts Magn. Reson. 2000;12:173-187.
- Watanabe H., Takaya N., Mitsumori F., Development of quantitative water content mapping in human brain at high magnetic field. Proc. Intl. Soc. Mag. Reson. Med. 2019;27:4406.
- Watanabe H., Takaya N., Mitsumori F. Non-uniformity correction of human brain at high field by RF field mapping of B1+ and B1-. J. Magn. Reson. 2011;212(2):426-430.
- Lee Y., Han Y., Park H.W., Watanabe H., Garwood M., Park J.Y. New phase-based B1 mapping method using two-dimensional spin-echo imaging with hyperbolic secant pulses. Magn. Reson. Med. 2015;73(1):170-181.
- Watanabe H. Experimental demonstration of the proportionality of the RF reception field to a complex conjugate of B1-. Magn. Reson. Med. Sci. 2012;11(3):193-196.
Figures
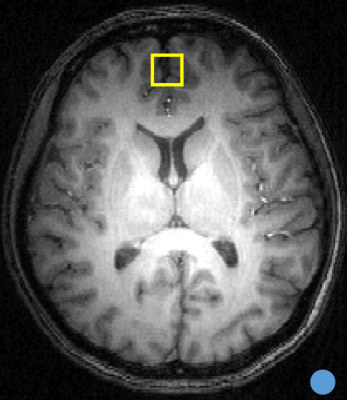
Fig. 1. Absolute quantitation in 1H MRS can be done using an external concentration reference (lite blue circle). However, reception sensitivities cannot be compared between the VOI (yellow square) and the external reference at high B0 field due to B1 inhomogeneity. The map of the reception sensitivity of B1- cannot be measured in a human brain at high B0 field.
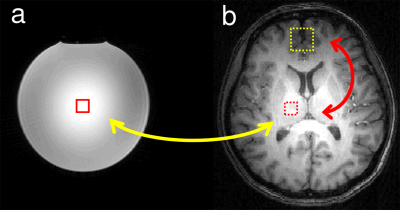
Fig. 2. In our proposed absolute quantitation method in 1H MRS, a water phantom as a concentration reference (a) and a human brain (b) are measured separately. The ratio of the reception sensitivities between the uniform areas (red squares) can be computed from the ratio of measured B1+s [3]. The reception sensitivity of the VOI (yellow dotted square) can be computed from that of the uniform area (red dotted square) by the ratio map method [4]. From these relationships, the reception sensitivities can be compared between the VOI in the human brain and the uniform area in the phantom.

Fig. 3. To demonstrate our proposed method, a cylinder phantom filled with water was used as a concentration reference phantom (a) and a spherical saline phantom instead of a human brain for measuring (b). The ratio of the reception sensitivities between the uniform area (red squares) was 0.526 from measured B1+s. The ratio of the reception sensitivity in the VOI (yellow dotted square) to the uniform area (red dotted square) was 0.776. Coef in Eq.3 was computed as 0.408. Then, the concentration in the VOI was 54.2 [M] using Eq.4 whose close to the water concentration of 55.5 [M].