2612
Variability from complexity: assessing IVIM acquisition schemes through parameter estimation uncertainty
Sean C Epstein1, Timothy J. P. Bray2, Margaret A. Hall-Craggs2, and Hui Zhang1
1Department of Computer Science & Centre for Medical Image Computing, University College London, London, United Kingdom, 2Centre for Medical Imaging, University College London, London, United Kingdom
1Department of Computer Science & Centre for Medical Image Computing, University College London, London, United Kingdom, 2Centre for Medical Imaging, University College London, London, United Kingdom
Synopsis
This work uses the quantification of parameter-estimation uncertainty to assess the clinical suitability of IVIM acquisition schemes. We apply this analysis to two bone marrow classification tasks. We simulate IVIM data and show that fitting a simplified, biased, diffusion model (ADC), can, under certain clinically relevant conditions, outperform ground-truth IVIM fitting. We further show that, within the same disease, the opposite can also be true: IVIM outperforms ADC. Such results can play an important role in guiding clinical DWI practice and we show that they can be predicted by explicitly quantifying the uncertainty in parameter estimation.
Introduction
Quantitative diffusion-weighted imaging (DWI) has, in recent years, been characterised by an increase in the complexity of the underlying biophysical models1,2. This change has transformed some fields, such as brain imaging, where new models have brought added microstructural insight3–6. In body DWI, IVIM has grown in popularity as a replacement for ADC7–12. Acknowledging that IVIM fitting depends on experimental design, a number of studies have attempted to optimise acquisition protocols for this model13–17. Despite this, in fields such as bone marrow imaging, IVIM studies have adopted a wide range of acquisition protocols18–28. There is presently a lack of understanding of the robustness of the parameter estimates arising from, and therefore the clinical suitability of, these acquisition schemes. This work uses the quantification of parameter-estimation uncertainty to assess such schemes, using bone marrow imaging as an example. This analysis is applied to two clinical classification tasks, where we demonstrate its value in predicting diffusion model performance and, by extension, in guiding clinical DWI practice.Methods
Parameter uncertainty was quantified by Monte Carlo simulation. Synthetic diffusion-weighted data were generated from the IVIM model29:$$ S(b) = S_0 (f e^{-b(D+D^*)} + (1-f)e^{-bD})$$ where model parameters were chosen to represent four distinct types of bone marrow, corresponding to sacroiliac joint lesions in patients with Ankylosing Spondylitis (AS) as well as healthy controls (Table 1)30; $$$S_0 = 1$$$ was used without loss of generality. These tissues were selected from reported clinical ranges30 to enable comparison between tissues differing in one parameter only: $$$D$$$ ($$$\alpha$$$ and $$$\beta$$$) or $$$f$$$ ($$$\gamma$$$ and $$$\delta$$$). The four signal profiles were corrupted by Rician noise at three levels (SNR 30, 60, 90). The signals were sampled 100,000 times using three published protocols representative of bone IVIM imaging (Table 2).
The ADC and IVIM models were fit to each set of experimental repeats. ADC fitting was performed on the log-transformed signal with weighted least-squares linear regression, a compromise between speed and accuracy31. IVIM fitting was performed with two of the most commonly used algorithms32: bound-constrained non-linear least squares (NLLS) and segmented NLLS ($$$D$$$ fixed by monoexponential fit, $$$S_0$$$, $$$f$$$ and $$$D^*$$$ obtained from NLLS). The boundary constraints were: $$$S_0 \in [0,2]$$$, $$$f \in [0,1]$$$, $$$D^* \in [0,500]$$$ 10-3 mm2/s, $$$D \in [0,10]$$$ 10-3 mm2/s. To reduce the likelihood of local minima, both NLLS fitting techniques were seeded with the ground-truth IVIM parameters.
Fitting uncertainty was assessed by generating the distribution of parameter estimates. The four tissues were analysed pairwise ($$$\alpha$$$/$$$\beta$$$, $$$\gamma$$$/$$$\delta$$$) by means of ROC curves to compare the sensitivity and specificity of IVIM and ADC fitting to either $$$D$$$ ($$$\alpha$$$/$$$\beta$$$ pair) or or $$$f$$$ ($$$\gamma$$$/$$$\delta$$$ pair) for each acquisition scheme.
Results & Discussion
Figure 1 compares the classification performance of ADC and IVIM between tissues differing in $$$D$$$ ($$$\alpha$$$ and $$$\beta$$$), representing active and chronic lesions respectively. ADC, a biased, simplified model, outperformed both IVIM fitting methods under all conditions. This result is explained by Figure 2, which shows the uncertainties arising from both ADC and segmented NLLS. Despite ADC giving upward-biased estimates of D, the estimation uncertainty (distribution width) was lower than that of segmented IVIM, resulting in better classification.Figure 3 again compares the classification performance of the two models, this time applied to differences in $$$f$$$ ($$$\gamma$$$ vs. $$$\delta$$$), corresponding to differentiating chronic lesions from healthy tissue. ADC does not estimate perfusion fraction directly, and $$$D$$$ is the only surrogate measure of $$$f$$$ available for this model. At low SNR, both models were poor classifiers. As SNR increased, IVIM performance improved drastically, with segmented fitting outperforming NLLS. This result is explained by Figure 4, which shows the estimation uncertainties of the classifiers: $$$f$$$ (IVIM) and $$$D$$$ (ADC). Both models were sensitive to changes in $$$f$$$, but IVIM’s direct parameter estimation was found to have higher CNR than ADC’s indirect surrogate classifier.
Conclusions
We demonstrate that fitting a biased, simplified ADC model can outperform more complex fitting, even when the ground truth (in this case IVIM) is known. We show this by comparing both models in a clinically relevant task, namely classifying active and chronic bone marrow lesions, where all IVIM parameters other than $$$D$$$ have been found to remain constant30.We further demonstrate that for other tasks – for example distinguishing chronic lesions from healthy tissue – the higher complexity IVIM model reliably outperforms ADC, although rich acquisition protocols are required for high-quality classification.
We show that insight can be gained into both results by means of Monte Carlo uncertainty quantification: it can be seen from parameter-estimation distributions that the additional microstructural nuance offered by IVIM fitting can, depending on clinical task, be outweighed by a corresponding increase in uncertainty.
We therefore argue that explicit uncertainty quantification is a powerful tool for guiding DWI practice and assessing the clinical suitability of IVIM experimental designs.
Acknowledgements
This work is supported by the EPSRC-funded UCL Centre for Doctoral Training in Medical Imaging (EP/L016478/1) and the Department of Health’s NIHR-funded Biomedical Research Centre at University College London Hospitals. TJPB is supported by an NIHR Clinical Lectureship.References
- Ni P, Lin Y, Zhong Q, Chen Z, Sandrasegaran K, Lin C. Technical advancements and protocol optimization of diffusion-weighted imaging (DWI) in liver. Abdom Radiol. 2016;41(1):189-202. doi:10.1007/s00261-015-0602-x
- Alexander DC, Dyrby TB, Nilsson M, Zhang H. Imaging brain microstructure with diffusion MRI: practicality and applications. NMR Biomed. 2019;32(4):e3841. doi:10.1002/nbm.3841
- Zhang H, Schneider T, Wheeler-Kingshott CA, Alexander DC. NODDI: Practical in vivo neurite orientation dispersion and density imaging of the human brain. Neuroimage. 2012;61(4):1000-1016. doi:10.1016/j.neuroimage.2012.03.072
- Assaf Y, Basser PJ. Composite hindered and restricted model of diffusion (CHARMED) MR imaging of the human brain. Neuroimage. 2005;27(1):48-58. doi:10.1016/j.neuroimage.2005.03.042
- Tournier J-D, Calamante F, Gadian DG, Connelly A. Direct estimation of the fiber orientation density function from diffusion-weighted MRI data using spherical deconvolution. Neuroimage. 2004;23(3):1176-1185. doi:10.1016/j.neuroimage.2004.07.037
- Jensen JH, Helpern JA, Ramani A, Lu H, Kaczynski K. Diffusional kurtosis imaging: The quantification of non-gaussian water diffusion by means of magnetic resonance imaging. Magn Reson Med. 2005;53(6):1432-1440. doi:10.1002/mrm.20508
- Noij DP, Martens RM, Marcus JT, et al. Intravoxel incoherent motion magnetic resonance imaging in head and neck cancer: A systematic review of the diagnostic and prognostic value. Oral Oncol. 2017;68:81-91. doi:10.1016/J.ORALONCOLOGY.2017.03.016
- Tian T, Zhang G-F, Zhang H, Liu H. Intravoxel incoherent motion diffusion-weighted imaging in differentiating uterine fibroid from focal adenomyosis: initial results. Springerplus. 2016;5(1):9. doi:10.1186/s40064-015-1635-x
- Liu C, Wang K, Chan Q, et al. Intravoxel incoherent motion MR imaging for breast lesions: comparison and correlation with pharmacokinetic evaluation from dynamic contrast-enhanced MR imaging. Eur Radiol. 2016;26(11):3888-3898. doi:10.1007/s00330-016-4241-6
- Klauss M, Mayer P, Maier-Hein K, et al. IVIM-diffusion-MRI for the differentiation of solid benign and malign hypervascular liver lesions—Evaluation with two different MR scanners. Eur J Radiol. 2016;85(7):1289-1294. doi:10.1016/J.EJRAD.2016.04.011
- Re TJ, Lemke A, Klauss M, et al. Enhancing pancreatic adenocarcinoma delineation in diffusion derived intravoxel incoherent motion f-maps through automatic vessel and duct segmentation. Magn Reson Med. 2011;66(5):1327-1332. doi:10.1002/mrm.22931
- Pesapane F, Patella F, Fumarola EM, et al. Intravoxel Incoherent Motion (IVIM) Diffusion Weighted Imaging (DWI) in the Periferic Prostate Cancer Detection and Stratification. Med Oncol. 2017;34(3):35. doi:10.1007/s12032-017-0892-7
- Cohen AD, Schieke MC, Hohenwalter MD, Schmainda KM. The effect of low b-values on the intravoxel incoherent motion derived pseudodiffusion parameter in liver. Magn Reson Med. 2015;73(1):306-311. doi:10.1002/mrm.25109
- Lemke A, Stieltjes B, Schad LR, Laun FB. Toward an optimal distribution of b values for intravoxel incoherent motion imaging. Magn Reson Imaging. 2011;29(6):766-776. doi:10.1016/J.MRI.2011.03.004
- Dyvorne H, Jajamovich G, Kakite S, Kuehn B, Taouli B. Intravoxel incoherent motion diffusion imaging of the liver: optimal b-value subsampling and impact on parameter precision and reproducibility. Eur J Radiol. 2014;83(12):2109-2113. doi:10.1016/j.ejrad.2014.09.003
- Leporq B, Saint-Jalmes H, Rabrait C, et al. Optimization of intra-voxel incoherent motion imaging at 3.0 Tesla for fast liver examination. J Magn Reson Imaging. 2015;41(5):1209-1217. doi:10.1002/jmri.24693
- Chen W, Zhang J, Long D, Wang Z, Zhu J-M. Optimization of intra-voxel incoherent motion measurement in diffusion-weighted imaging of breast cancer. J Appl Clin Med Phys. 2017;18(3):191-199. doi:10.1002/acm2.12065
- Sun H, Liu K, Liu H, et al. Comparison of bi-exponential and mono-exponential models of diffusion-weighted imaging for detecting active sacroiliitis in ankylosing spondylitis. Acta radiol. 2018;59(4):468-477. doi:10.1177/0284185117722811
- Zuo H. The Value of Intravoxel Incoherent Motion (IVIM) Magnetic Resonance Imaging in the Evaluation of the Osteosarcoma Response to Preoperative Neoadjuvant Chemotherapy in Teens. Concepts Magn Reson Part A. 2019;2019:1-8. doi:10.1155/2019/2918763
- Marchand AJ, Hitti E, Monge F, et al. MRI quantification of diffusion and perfusion in bone marrow by intravoxel incoherent motion (IVIM) and non-negative least square (NNLS) analysis. Magn Reson Imaging. 2014;32(9):1091-1096. doi:10.1016/J.MRI.2014.07.009
- Wu G, Xie R, Liu X, Hou B, Li Y, Li X. Intravoxel incoherent motion diffusion MR and diffusion kurtosis imaging for discriminating atypical bone metastasis from benign bone lesion. Br J Radiol. 2019;92(1100):20190119. doi:10.1259/bjr.20190119
- Park S, Kwack K-S, Chung N-S, Hwang J, Lee HY, Kim JH. Intravoxel incoherent motion diffusion-weighted magnetic resonance imaging of focal vertebral bone marrow lesions: initial experience of the differentiation of nodular hyperplastic hematopoietic bone marrow from malignant lesions. Skeletal Radiol. 2017;46(5):675-683. doi:10.1007/s00256-017-2603-z
- Bourillon C, Rahmouni A, Lin C, et al. Intravoxel Incoherent Motion Diffusion-weighted Imaging of Multiple Myeloma Lesions: Correlation with Whole-Body Dynamic Contrast Agent–enhanced MR Imaging. Radiology. 2015;277(3):773-783. doi:10.1148/radiol.2015141728
- Shah R, Stieltjes B, Andrulis M, et al. Intravoxel incoherent motion imaging for assessment of bone marrow infiltration of monoclonal plasma cell diseases. Ann Hematol. 2013;92(11):1553-1557. doi:10.1007/s00277-013-1786-1
- Ohno N, Miyati T, Kasai H, et al. Evaluation of perfusion-related and true diffusion in vertebral bone marrow: a preliminary study. Radiol Phys Technol. 2015;8(1):135-140. doi:10.1007/s12194-014-0301-2
- Yeung DKW, Wong SYS, Griffith JF, Lau EMC. Bone marrow diffusion in osteoporosis: Evaluation with quantitative MR diffusion imaging. J Magn Reson Imaging. 2004;19(2):222-228. doi:10.1002/jmri.10453
- Chen Y, Yu Q, La Tegola L, et al. Intravoxel incoherent motion MR imaging for differentiating malignant lesions in spine: A pilot study. Eur J Radiol. 2019;120:108672. doi:10.1016/J.EJRAD.2019.108672
- Yoon MA, Hong S-J, Lee CH, Kang CH, Ahn K-S, Kim BH. Intravoxel incoherent motion (IVIM) analysis of vertebral bone marrow changes after radiation exposure from diagnostic imaging and interventional procedures: http://dx.doi.org/101177/0284185116688380. January 2017. doi:10.1177/0284185116688380
- Le Bihan D, Breton E, Lallemand D, Aubin ML, Vignaud J, Laval-Jeantet M. Separation of diffusion and perfusion in intravoxel incoherent motion MR imaging. Radiology. 1988;168(2):497-505. doi:10.1148/radiology.168.2.3393671
- Zhao Y, Li S, Liu Z, et al. Detection of Active Sacroiliitis with Ankylosing Spondylitis through Intravoxel Incoherent Motion Diffusion-Weighted MR Imaging. Eur Radiol. 2015;25(9):2754-2763. doi:10.1007/s00330-015-3634-2
- Jones DK, Basser PJ. “Squashing peanuts and smashing pumpkins?”: How noise distorts diffusion-weighted MR data. Magn Reson Med. 2004;52(5):979-993. doi:10.1002/mrm.20283
- Suo S, Lin N, Wang H, et al. Intravoxel incoherent motion diffusion-weighted MR imaging of breast cancer at 3.0 tesla: Comparison of different curve-fitting methods. J Magn Reson Imaging. 2015;42(2):362-370. doi:10.1002/jmri.24799
Figures
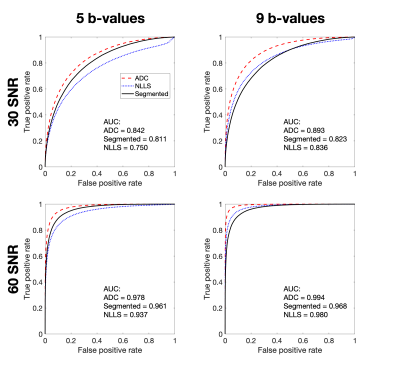
Figure 1 – ROC curves for $$$\alpha$$$/$$$\beta$$$ classification task using estimates of $$$D$$$, comparing performance of ADC and IVIM fitting. ADC outperformed both IVIM fits for all combinations of SNR and b-values. Classification performance for 120 SNR and/or 14 b-values is not shown as AUC = 1 for all three fitting methods.

Figure 2 – Distribution of $$$D$$$ estimates for $$$\alpha$$$ and $$$\beta$$$, arising from ADC and segmented IVIM fitting. Segmented fitting results are representative of constrained NLLS (not shown). Each distribution was approximated by a Gaussian (not shown); mean and standard deviation are reported. ADC estimates of $$$D$$$ were found to be upward-biased but had lower uncertainty and higher CNR.

Figure 3 – ROC curves for $$$\gamma$$$/$$$\delta$$$ classification task using either estimates of $$$f$$$ (IVIM fitting) or $$$D$$$ (ADC fitting). A representative subset of SNR and b-values is shown: results for 60 SNR and/or 9 b-values can be interpolated from what is reported here. Segmented IVIM fitting outperformed ADC for all combinations of SNR and b-values.
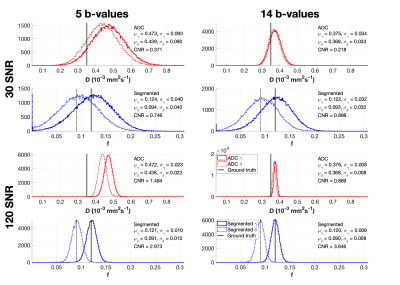
Figure 4 – Distribution of parameter estimates for $$$\gamma$$$ and $$$\delta$$$, arising from ADC and segmented IVIM fitting. Segmented fitting results are representative of constrained NLLS (not shown). Each distribution was approximated by a Gaussian (not shown); mean and standard deviation are reported. ADC estimates of $$$D$$$ were found to have lower CNR than IVIM estimates of $$$f$$$.

Table 1 – simulated tissue parameter values, representative of AS pathology30

Table 2 – b-value acquisition protocols representative of published bone IVIM imaging