Introduction

Quantitative T₁ mapping is an emerging quantitative biomarker of hepatic fibrosis^1,2,3 and liver function⁴. Conventional methods for T₁ mapping in the liver include variable flip angle strategies with additional multi-echo spoiled gradient echo (SGRE) acquisitions to account for the tissue fat^5,6. However, VFA methods are sensitive to B₁ inhomogeneities and require a separate calibration scan to correct the estimation errors⁷. Furthermore, Cartesian sampling trajectories are limited to breath-holding approaches to avoid motion related ghosting artifacts, which may limit their use in children, the elderly and sick patients.

Therefore, the purpose of this work is to develop and validate a novel method for T₁ mapping in the liver, that takes advantage of motion insensitivity of 3D-radial acquisition and is capable of addressing multiple confounding factors. The proposed method combines 3D-radial inversion recovery and multi-echo SGRE sequences with variable flip angles and echo times to simultaneously estimate T₁ of water (T_1w), T₁ of fat (T_1f), proton density fat fraction (PDFF), and B₀ and B₁ inhomogeneities using a multi-compartment fitting strategy.

Theory

Inversion recovery-based acquisitions are popular for T₁ mapping strategies due to the excellent dynamic range in T₁ recovery created by inversion of the longitudinal magnetization. A recently published work by Kecskemeti et al. described an efficient way of collecting an arbitrarily large number of T₁ weighted images using a 3D-radial inversion recovery sequence⁸ called ”MPnRAGE”. This method was shown to be capable of obtaining 3D volumetric T₁ maps in the brain. Here, we extend this method to acquire multi-echo SGRE images to account for effects of tissue fat. In this work, we use a 2-compartment signal model for fat and water (each with independent T₁ relaxation, inversion pulse efficiency, and initial phase), while fitting for a 6-peak fat⁹. Assuming perfect spoiling between each excitation RF pulse, we can describe the signal equation as follows:
$$S_{w,MPnRAGE}(TI,TR,TD,\alpha;T_{1,w},\kappa_1,\kappa_{2,w})=((1-E_{R,w})\cdot~\frac{1-a_w^n}{1-a_w}+((1-E_{I,w})+M_{SS,w}(E_{D,w})\cdot~cos(\kappa_{2,w}\cdot~180)\cdot~E_{I,w})\cdot~a_w^n)\cdot~sin(\kappa_1\cdot~\alpha)$$
$$S_{f,MPnRAGE}(TI,TR,TD,\alpha;T_{1,f},\kappa_1,\kappa_{2,f})=((1-E_{R,f})\cdot~\frac{1-a_f^n}{1-a_f}+((1-E_{I,f})+M_{SS,f}(E_{D,w})\cdot~cos(\kappa_{2,f}\cdot~180)\cdot~E_{I,f})\cdot~a_f^n)\cdot~sin(\kappa_1\cdot~\alpha)$$
$$S_{w,SGRE}(TE;\theta_w,\Delta B_0,T_2^*,\rho_w)=\rho_w\cdot~e^{-TE/T_2^*}\cdot~e^{i(\theta_w+2\pi~f_0TE)}$$
$$S_{f,SGRE}(TE;\theta_f,\Delta B_0,T_2^*,\rho_f)=\rho_f\cdot~e^{-TE/T_2^*}\cdot~e^{i(\theta_f+2\pi~f_0TE)}\cdot~\sum_{p=1}^P m_p\cdot~e^{i2\pi f_pTE}$$
$$E_{R(w,f)}=e^{-TR/T_{1(w,f)}},E_{I(w,f)}=e^{-TI/T_{1(w,f)}},E_{D(w,f)}=e^{-TD/T_{1(w,f)}},a_{(w,f)}=cos(\kappa_1\cdot \alpha)\cdot E_{R(w,f)}$$
$$S_{combined}=S_{w,MPnRAGE}\cdot~S_{w,SGRE}+S_{f,MPnRAGE}\cdot~S_{f,SGRE}$$
Where, subscripts 'w' and 'f' denote signal parameters for water and fat signals, 'n' denotes the index of the excitation pulse in the inversion recovery sequence, $$$M_{SS,(w,f)}$$$ denotes the longitudinal magnetization at the end of one inversion recovery cycle, $$$\rho_{w,f}$$$ denotes signal amplitudes, $$$\theta_{w,f}$$$ denotes initial phase, $$$\kappa_1$$$ and $$$\kappa_{2(w,f)}$$$ denote efficiencies of excitation and inversion RF pulses (note for adiabatic pulses, due to duration of the pulse efficiency may differ between fat and water), $$$f_0$$$ denotes the frequency shift due to B₀ inhomogeneity.
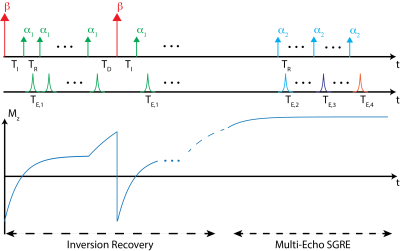
A diagram of the proposed pulse sequence is given in Figure 1, where $$$\beta$$$ denotes the inversion and $$$\alpha$$$ denotes the excitation pulses. TE_i denotes the echo time corresponding to I^th SGRE acquisition.

Methods

Numerical Simulations
The proposed acquisition and 2-compartment joint fitting method were tested using simulation data over a wide range of physiologically relevant liver T_1w (300-1100ms) and PDFF (0-50%) values. Other simulation parameters include: $$$T_2^*=15ms$$$, $$$\kappa_1=0.95$$$, $$$\kappa_{2w,f}=0.87$$$, $$$T_{1f}=270ms$$$, $$$\Delta~B0=1ppm$$$. Acquisition parameters are chosen as follows, $$$\beta=180^o$$$,$$$\alpha_1=4^o$$$, $$$\alpha_2=8^o$$$, TE₁=0.86ms, TE₂=1.12ms, TE₃=1.52ms, TE₄=2.32ms, TR=5ms, T_I=15ms, T_D=500ms (see fig.1), SNR=25. Since signal amplitude varies over the acquisition, SNR is defined as maximum signal amplitude in the acquired signal divided by the standard deviation of the noise.

Phantom Experiments
Two sets of phantoms experiments are presented to demonstrate validation of the T₁ mapping accuracy and feasibility of correction for tissue fat.
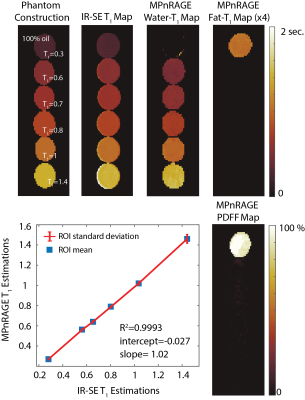
For the validation study, a single compartment phantom, consisting of 5 doped water vials with varying T₁ values and one oil vial, was used. Since single compartment nature of the phantom allows for a magnitude fitting without correction of partial volume effects, this phantom was also scanned with an inversion recovery spin echo (IR-SE) sequence at varying TIs to provide a reference measurement.
For the feasibility study, a phantom consisting of varying fat fractions (5-60%) and 2 different T_1w values (obtained by addition of various amount of CuSO₄ salt) was used. Imaging was performed with the high density, multi-channel body coil on a 3T system (AIR Coil, GE Healthcare Signa Premier, Waukesha, WI).

Results

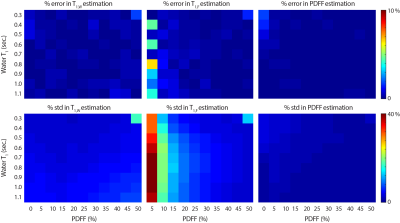
Numerical Simulations
Monte-Carlo simulations demonstrated the proposed strategy converges to unbiased estimators for all parameters of interest. Figure 2 shows the median and standard deviations of estimated T_1w, T_1f and PDFF.

Phantom Experiments
Validation of the proposed method is shown in Figure 3, where, estimated T_1w and T_1f values show linear agreement with IR-SE acquisitions.
Feasibility for fat-correction of the proposed method is demonstrated by joint estimation of PDFF and T_1f in Figure 4. Estimated T_1w values showed good agreement with CuSO₄ concentrations, and PDFF values showed linear agreement with ground truth values.

Discussion

In this work, we have successfully presented a novel acquisition and fitting strategy for T₁ mapping in the liver, that can jointly estimate and correct for multiple confounding factors including B₀ and B₁ inhomogeneities and tissue fat. This strategy combines an inversion-recovery based T₁ mapping technique (MPnRAGE) and multi-echo SGRE to modulate T₁, T₂* contrasts and spin phase for simultaneous estimation of multiple confounding parameters. Future work will focus on improving the acquisition strategy to increase efficiency and account for T₂* effects, and optimization of acquisition parameters.

Acknowledgements

We wish to acknowledge support from the NIH (R01 DK083380, R01 DK088925, K24 DK102595, UL1TR002373) and from the University of Wisconsin SEED grant program. Further, we wish to acknowledge GE Healthcare and Bracco Diagnostics who provides research support to the University of Wisconsin. Finally, Dr. Reeder is a Romnes Faculty Fellow, and has received an award provided by the University of Wisconsin-Madison Office of the Vice Chancellor for Research and Graduate Education with funding from the Wisconsin Alumni Research Foundation.