Introduction

MR imaging and spectroscopy of ¹²⁹Xe dissolved in pulmonary red blood cells (RBCs) and parenchymal tissue/plasma (TP) is of interest for investigating gas (G) exchange dynamics in a range of pulmonary pathologies^1,2,3. Key to the success of dissolved-phase ¹²⁹Xe spectroscopy and imaging is the ability to reliably measure the signal amplitude and chemical shift of ¹²⁹Xe in RBCs and TP within an MR acquisition. While previous studies considered dissolved-phase ¹²⁹Xe spectra as consisting of two simple Lorentzian RBC and TP resonances, recent work with time-domain (TD) Voigt fitting suggests that the TP resonance is more structured with a measurable Gaussian component to its linewidth⁴ . Within this study we evaluate the accuracy of fitting the G, RBC and TP ¹²⁹Xe resonances with a TD Voigt function over a range of SNR values by comparing fitted peak parameters with peak parameters from synthetically generated FIDs.

Methods

The time-domain Voigt function $$$\nu(t)$$$ used for data fitting to the real and imaginary parts of the synthetic FIDs is given by$$Re[\nu(t)]=\sum_{n=1}^3A_{n}\exp(-\pi\Gamma_{n}^lt)\exp\left[-\left(\frac{\pi\Gamma_{n}^gt}{2\sqrt{\ln2}}\right)^2\right]\cos[(\omega_{0,n}-\omega_{t})t+\phi_{n}]\quad\quad\quad \\ Im[\nu(t)]=\sum_{n=1}^3A_{n}\exp(-\pi\Gamma_{n}^lt)\exp\left[-\left(\frac{\pi\Gamma_{n}^gt}{2\sqrt{\ln2}}\right)^2\right]\sin[(\omega_{0,n}-\omega_{t})t+\phi_{n}]\quad\quad(1)$$ where $$$A$$$ is FID the amplitude, $$$\Gamma^{l}$$$ and $$$\Gamma^{g}$$$ are Lorentzian and Gaussian linewidths, $$$\omega_0-\omega_{t}=\Delta\omega$$$ is frequency difference between the resonance frequency and RF transmit frequency and $$$\phi$$$ is the phase of the $$$n=$$$(G,TP,RBC) ¹²⁹Xe resonant peaks. (N.B. For a given time-domain Gaussian function defined by $$$g(t)=A\exp(-t^2/2\sigma_t^2)$$$, where $$$\sigma_t^2$$$ describes the TD width, it possible to replace $$$\sigma_{t}$$$ for the FWHM $$$\Gamma^g=\sqrt{2\ln{2}}/\pi\sigma_t$$$ of the corresponding FD Gaussian function $$$G(f)=A\sigma_t\sqrt{2\pi}\exp[-2(\pi\sigma_tf)^2]$$$ s.t the TD Gaussian function is written as $$$g(t)=A\exp[-(\pi\Gamma^gt/2\sqrt{\ln2})^2]$$$.)

FIDs (BW $$$=$$$ 16 kHz, samples $$$=$$$ 512) were generated in MATLAB with fixed RBC ($$$A=$$$ 0.25, $$$\Gamma^l=$$$ 180 Hz, $$$\Gamma^g=$$$ 0 Hz, $$$\phi=-$$$ 1.94 rad, $$$\Delta\omega=-$$$778 rad^-1) and TP ($$$A=$$$ 0.5, $$$\Gamma^l=$$$ 150 Hz, $$$\Gamma^g=$$$ 100 Hz, $$$\phi=-$$$ 0.55 rad, $$$\Delta\omega=$$$1,221 rad^-1) peak parameters and variable G amplitudes ($$$A=$$$ 0.1 to 1, $$$\Gamma^l=$$$25 Hz, $$$\Gamma^g=$$$ 0 Hz, $$$\phi=$$$ 0.13 rad, $$$\Delta\omega=$$$ 23,190 rad^-1 ). Complex Gaussian white noise ranging from $$$N=5\times10^{-4}$$$ to $$$2.5\times10^{-2}$$$ (SD in real part of time domain) was added to all FIDs. 50 synthetic FIDs with varying G amplitudes and noise levels were generated resulting in a total of 50×20×21 = 21,000 (20 noise values, 21 G amplitudes) to be fitted with Eq. 1 using the non-linear Levenberg-Marquardt least squares algorithm. The accuracy of each fitted parameter was calculated from the mean absolute percentage error $$ M=\frac{100\%}{n}\sum^n_{t=1}\vert\frac{A_{t}-F_{t}}{A_t}\vert \quad\quad (2) $$ where $$$n=$$$ 50 FIDs, and $$$A_{t}$$$ and $$$F_{t}$$$ are the actual and fitted values of the peak parameters for varying noise levels and G amplitudes. The initial parameter guesses prior to fitting were as follows: RBC peak: $$$A=$$$ 0.5, $$$\Gamma^l=$$$ 100 Hz, $$$\Gamma^g=$$$ 0 Hz, $$$\phi=$$$ 0 rad, $$$\Delta\omega=-$$$500 rad^-1; TP peak $$$A=$$$ 0.5, $$$\Gamma^l=$$$ 100 Hz, $$$\Gamma^g=$$$ 100 Hz, $$$\phi=$$$ 0 rad, $$$\Delta\omega=$$$ 1,000 rad^-1 ; G peak: $$$A=$$$ 0.5, $$$\Gamma^l=$$$ 10 Hz, $$$\Gamma^g=$$$ 0 Hz, $$$\phi=$$$ 0 rad, $$$\Delta\omega=$$$ 20,000 rad^-1.

Results and Discussion

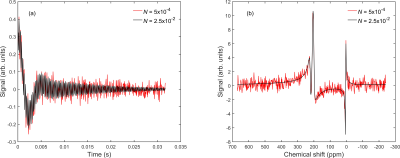
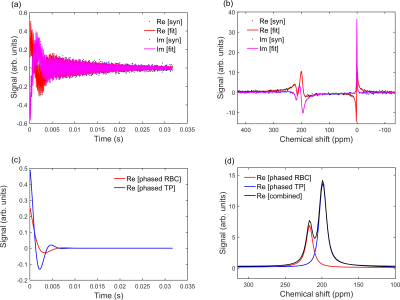
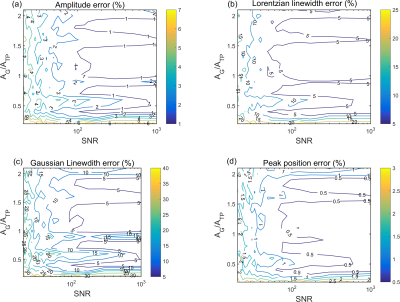
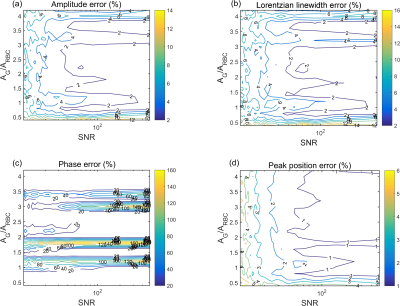
Fig. 1 (a) and (b) show synthetic FIDs in the time- and frequency-domain, respectively for the lower ($$$N=5\times10^{-4}$$$) and upper ($$$2.5\times10^{-2}$$$ ) noise levels and a G amplitude of 0.2. Fig. 2 shows a representative Voigt fit for a noise level of 0.0113 (TP SNR = 44, RBC SNR = 22). The mean absolute percentage error of the fitted TP, RBC ¹²⁹Xe peak parameters are shown as contour plots in Figs. 3 and 4, respectively.
The contour plots from the TP resonance show that all peak parameters have <5% error for SNR values >100 and a G:TP ratio of ~1.25; the contour plots from the RBC resonance show that the all peak parameters have <5% error for SNR values >100 and a G:TP ratio of ~2.5. For both TP and RBC resonances, the highest error in peak parameters is for low gas amplitudes, suggesting an inherent error in the fitting routine when the intial guess for the gas amplitude is much higher than the actual gas amplitude. For SNRs below 100, the parameter with the largest fitting error for the TP resonance is the Gaussian linewidth, which has an error of 15-20% for SNR values lower than 50.

The data in Figs. 3 and 4 show that if that gas amplitude is a factor of ~2 higher, there is a resulting error of >5% for all TP peak parameters at SNRs <100 and a resulting error of >5% for all RBC peak parameters at all SNR values. Fig 4 (c) shows a high intermittent error in the phase for the RBC resonance, which is most likely due to the initial guess for the RBC phase of 0 rad being far away from the actual phase of -1.94 rad, suggesting error sensitivity to poor initial guess for the RBC phase. Further work quantifying the effect of the initial starting guess on peak parameter accuracy prior to fitting is underway.

Conclusions

It has been shown that time-domain Voigt fitting results in <5% error for ¹²⁹ Xe TP and RBC peak parameters for SNR values of >100 and gas:dissolved amplitude ratios of <2. This work should enable accuracy quantification of TP and RBC >¹²⁹Xe resonances for any ongoing in vivo spectroscopy studies of ¹²⁹ Xe in the lungs.