2310
Low-rank and sparse matrix decomposition for accelerated non-contrast-enhanced functional lung MRI1Computer Assisted Clinical Medicine, Heidelberg University, Mannheim, Germany
Synopsis
Lung functions have significant clinical value for diagnosis of pulmonary diseases. Fourier Decomposition is a non-contrast-enhanced method for assessing pulmonary functions from time-resolved images. However, its performance depends on temporal resolution. Here we propose two compressed sensing reconstruction strategies based on low-rank and sparse matrix decomposition. Retrospective demonstrations on in vivo acquisitions demonstrate the performance of these techniques, enabling improved scan efficiency without degrading image quality.
Introduction
Assessment of pulmonary functions has significant clinical value for diagnosis of pulmonary diseases and can be helpful for follow-up investigations1. Although the gold standard for functional lung imaging depends on methods using radioactive nuclides, MRI based methods are highly desirable and promise great clinical utility2. To this end, Fourier Decomposition (FD) MRI method was demonstrated to be a useful non-ionizing and non-contrast-enhanced method capable of achieving local functional ventilation and perfusion information during free breathing3. This method utilizes 2D fast imaging sequences to obtain time-resolved images during free breathing. Afterwards, these images are registered and analyzed voxel-wise using Fourier transform to obtain periodic signal variations corresponding to respiratory and cardiac signal modulations, consequently enabling ventilation- and perfusion-weighted images.Although numerous studies have validated the FD method against well-established methods, its robustness depends on temporal resolution4. Some recent studies have proposed using compressed sensing approaches to improve the acquisition time and consequently the temporal resolution5,6. However, these methods can suffer from elevated interference at higher acceleration rates. In this work, we propose two new reconstruction strategies based on low-rank and sparse matrix decomposition. In vivo results are presented to demonstrate the performance and feasibility of the proposed strategies.
Methods
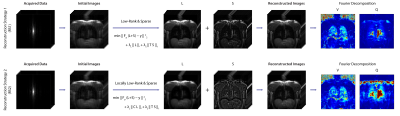
2D balanced steady-state free precession images were acquired from two healthy volunteers during free-breathing using a 1.5 T scanner (Magnetom Avanto, Siemens Healthineers, Erlangen, Germany). Two datasets were obtained using TR/TE = 1.88/0.8ms, slice thickness 15mm, matrix size = 128X128, bandwidth = 1302 Hz/Px, FA = 50°; and a third dataset was obtained using TR/TE = 2.13/0.92ms, matrix size = 192X192, FA = 30°. For all datasets, a total of 210 images were acquired with 100ms pause between measurements. Datasets were retrospectively undersampled in the phase encoding dimension to yield acceleration rates (R) between 2 to 6. Sampling masks were generated using variable density random sampling with different sampling pattern at each time point to extent k-space coverage7. Afterwards, undersampled data were reconstructed using two proposed approaches. General workflows can be seen at Figure 1. Our first proposed reconstruction strategy (RS1) obtains reconstructions by solving the following optimization problem based on low-rank plus sparse matrix decomposition8:$$\min\parallel F_p\cdot(L+S)-y\parallel^2_2+\lambda_L\parallel L \parallel_*+\lambda_S\parallel T\space S\parallel_1$$ Here, $$$F_p$$$ is Partial Fourier operator, $$$L+S$$$ is the reconstruction with $$$L$$$ and $$$S$$$ representing low-rank and sparse components respectively. $$$y$$$ is acquired k-space, $$$\lambda_L$$$ and $$$\lambda_S$$$ are empirically selected regularization weights, and $$$T$$$ represents temporal total variation as the sparsifying transform. The second reconstruction strategy (RS2), utilizes a locally low-rank approach9:
$$\min\parallel F_p\cdot(L+S)-y\parallel^2_2+\lambda_L\parallel C\space L\parallel_*+\lambda_S\parallel T\space S\parallel_1$$ Where $$$C$$$ acts as an operator that reformats $$$L$$$ into its Casorati form. The neighborhood size for local low rank was empirically selected as 4. For both approaches, the S-component represents the dynamics of the images, which contains information needed for ventilation- and perfusion-weighted images and L-component contains slowly-varying features, which are needed for registration purposes. Following the nonlinear reconstructions, the images were registered using a stand-alone non-rigid registration software10.
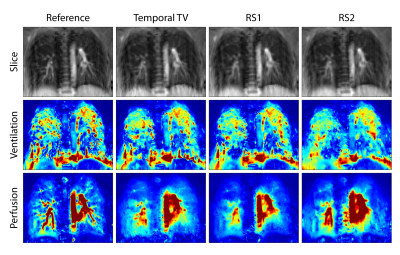
To comparatively demonstrate reconstructions, we have implemented the previously reported approach based on temporal total variation alone5. The reconstruction strategies were compared based on peak signal to noise ratio (PSNR), structural similarity index metric (SSIM) calculated over reconstructions. For all comparisons, fully sampled reference data (R=1) was taken as the reference, and the number of iterations were kept same among all reconstruction strategies.
Results
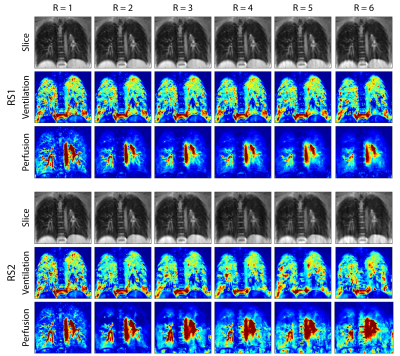
Table 1 shows PSNR and SSIM metrics. These values were calculated across all reconstructed slices after normalization. Figure 2 shows a reference slice with ventilation- and perfusion-weighted images for a single subject across acceleration rates, where R=1 denotes the reference case. Although RS2 performs worse in terms of PSNR and SSIM metrics, it is able to maintain perfusion information at higher acceleration rates. Figure 3 shows the comparison of different reconstruction strategies with the reference case at R=5. In ventilation maps, all methods achieve similar performance, although all methods suffer from interference artifacts and registration errors. This is further pronounced in regions closer to the diaphragm. In perfusion maps, temporal total variation method suffers from blurring, while RS1 and RS2 are able to display finer structures. Overall, our results indicate that low-rank based reconstructions can be utilized to improve the reconstruction quality and may enable higher undersampling factors in functional lung imaging.Discussion and Conclusion
In this work, we have developed and demonstrated two reconstruction strategies for functional lung imaging. We used retrospective undersampling to show the feasibility and performance of proposed methods. While we did not utilize any special sampling mask design, it might improve the reconstruction quality, especially for prospective studies11. Our initial observations indicate that the locally low rank approach decomposes the images more successfully, while the global low rank approach is less sensitive to regularization weight selection. Future studies are warranted investigating a combination of the two proposed methods, since the S- and L-components can be obtained separately. In summary, our results indicate that the proposed methods can improve the reconstruction quality and can enable higher acceleration rates for free breathing non-contrast-enhanced functional lung imaging studies. These techniques promise higher temporal resolution with increased clinical value for the diagnosis and follow-up of pulmonary diseases.Acknowledgements
This work was supported by Deutsche Forschungsgemeinschaft (grant number: DFG 397806429).References
1.Weis, M. et al. Lung perfusion MRI after congenital diaphragmatic hernia repair in 2-year-old children with and without extracorporeal membrane oxygenation therapy. American Journal of Roentgenology 206, 1315–1320 (2016).
2.Nyilas, S. et al. Novel magnetic resonance technique for functional imaging of cystic fibrosis lung disease. European Respiratory Journal 50, (2017).
3. Bauman, G. et al. Non-contrast-enhanced perfusion and ventilation assessment of the human lung by means of Fourier decomposition in proton MRI. Magnetic Resonance in Medicine 62, 656–664 (2009).
4. Kjørstad, Å. et al. Quantitative lung ventilation using Fourier decomposition MRI; comparison and initial study. Magnetic Resonance Materials in Physics, Biology and Medicine 27, 467–476 (2014).
5. Ilicak E. et al. Compressed Sensing reconstruction in non-contrast-enhanced functional lung MRI using Fourier Decomposition: An initial study Proceedings of the ISMRM 27th Annual Meeting & Exhibition, 1897 (2019).
6. Voskrebenzev, A. et al. Real-Time Imaging during Free Breathing for Patient-Friendly V/Q Scan of the Whole Lung in One Minute at 3T. Proceedings of the ISMRM 27th Annual Meeting & Exhibition, 4081 (2019).
7. Lustig, M., Santos, J. M., Donoho, D. & Pauly, J. M. k-t SPARSE: high frame rate dynamic MRI exploiting spatio-temporal sparsity. Proceedings of ISMRM, Seattle 50, 2420 (2006).
8. Otazo, R., Candès, E. & Sodickson, D. K. Low-rank plus sparse matrix decomposition for accelerated dynamic MRI with separation of background and dynamic components. Magnetic Resonance in Medicine 73, 1125–1136 (2015).
9. Yaman, B., Weingartner, S., Kargas, N., Sidiropoulos, N. D. & Akcakaya, M. Low-Rank Tensor Models for Improved Multi-Dimensional MRI: Application to Dynamic Cardiac T1 Mapping. IEEE Transactions on Computational Imaging 1–1 (2019). doi:10.1109/tci.2019.2940916
10. Chefd’hotel, C., Hermosillo, G. & Faugeras, O. Flows of diffeomorphisms for multimodal image registration. in Proceedings - International Symposium on Biomedical Imaging 2002-January, 753–756 (IEEE Computer Society, 2002).
11. Ahmad, R. et al. Variable density incoherent spatiotemporal acquisition (VISTA) for highly accelerated cardiac MRI. Magnetic Resonance in Medicine 74, 1266–1278 (2015).
Figures