Introduction

The scan time of phase contrast (PC) flow MRI is long due to the requirements of multiple acquisitions with varying bipolar gradients as well as high spatial and temporal resolution. Various scan acceleration techniques have been applied in PC MRI including compressed sensing (CS) reconstruction [1-4]. In this study, we develop a reconstruction algorithm which can improve CS-based reconstruction from under-sampled PC data.

Methods

Magnitude difference regularized compressed sensing
In PC MRI, since the reference and the bipolar encoded sequences have identical sequence parameters except the bipolar gradients, magnitude images should be similar to each other. This magnitude similarity can be utilized as a source of information redundancy and realized in the form of regularization. Compressed sensing reconstruction with multi-channel receive coils is typically formulated as unconstrained minimization of the following cost function.

C^(j) = ∑_i || y_i^(j) - F_uS_i m^(j) ||² + α||Ψm^(j) ||₁ j=1,...,N_v

where m^(j) is a complex image obtained by applying j^th velocity-encoded bipolar gradient. N_v is the number of bipolar gradients. y_i^(j) is the k-space data received through the i^th coil element when j^th bipolar gradient is applied, N_c is the number of coil elements, S_i is i^th coil sensitivity, and Ψ is a sparsifying transform and set to the total variation operation in this study. The penalization of magnitude difference among different velocity-encoded data can be incorporated into the compressed sensing formulation to yield the following cost function

C = ∑_j ∑_i || y_i^(j) - F_uS_i m^(j) ||2 + α||Ψm_(j) ||₁ +β|| |m_(j)| - |m_(j+1)| ||²

The new regularization term enforces magnitude similarity across different velocity-encoded images in the same spatial pixel while CS regularization enforces the similarity across neighboring pixels in the same velocity encoding. The cost function was minimized using a conjugate gradient method with line search.

In-vivo experiments
Phase contrast flow MRI was performed in seven healthy subjects for retrospective evaluation of the performance of the magnitude difference regularization. One-dimensional through-plane flow velocity was measured with 2D axial scan planes placed on subjects’ thighs (i.e., Nv = 2). Imaging parameters included VENC = 80 cm/s, spatial resolution = 1.0×1.0 mm2, FOV = 36×22 cm2, and temporal resolution = 20.6 ms. the addition of magnitude regularization was compared with CS only reconstruction by setting β to 0 (CS only) and 10^-4 during the image reconstruction.
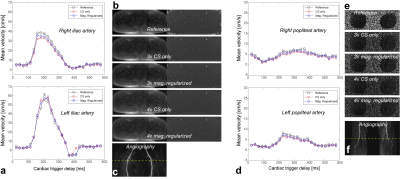
PC flow MRI was performed in a 52-year-old male patient with bilateral claudication. One-dimensional through-plane velocity measurement was performed twice, one for imaging the iliac arteries and the other for popliteal arteries. Imaging parameters were VENC = 90 cm/s, spatial resolution = 1.2×1.7 mm2 and FOV = 36×26 cm2 for measuring iliac flow velocity, and VENC = 60 cm/s, spatial resolution = 1.2×1.2 mm2 and FOV = 36×16 cm2 for measuring popliteal flow velocity. Rate-3 and rate-4 scan accelerations were implemented in a similar fashion to the healthy volunteer studies.

Results

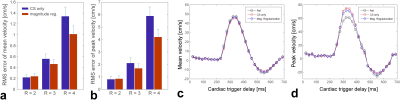
The comparisons between CS-only reconstruction and magnitude-regularized CS reconstruction are summarized in Figs. 1a and 1b. Over 360 ROIs, the RMS errors of mean velocities for the two reconstructions were 0.22±0.05 (CS only) / 0.24±0.06 (magnitude regularized) cm/s for two-fold acceleration (R=2), 0.56±0.09 / 0.46±0.08 cm/s for three-fold acceleration (R=3) and 1.34±0.17/ 1.08±0.15 cm/s for four-fold acceleration (R=4). The RMS errors of peak velocities were 0.65±0.23 (CS only) / 0.68±0.24 (magnitude regularized) cm/s for R=2, 2.11±0.42 / 1.69±0.36 cm/s for R=3, and 5.89±0.72/ 4.21±0.63 cm/s for R=4. Figures 1c and 1d show representative mean and peak velocities obtained for acceleration factor of 3.
Figure 2 contains the result of patient studies, displaying the time-curves of the mean flow velocities of 4-fold accelerated data (Figs. 2a and 2d for popliteal and popliteal arteries respectively), and raw images reconstructed from different regularization and acceleration conditions (Figs. 2b and 2e). Over 60 ROIs on the iliac arteries, the RMS errors of mean velocities were 0.72±0.12 (CS only) / 0.56±0.10 cm/s (magnitude regularized) for three-fold acceleration, and 1.75±0.21/ 1.24±0.19 cm/s for four-fold acceleration. Over 60 ROIs on the popliteal arteries, the RMS errors of mean velocities were 0.61±0.10 (CS only) / 0.42±0.11 cm/s (magnitude regularized) for three-fold acceleration, and 1.41±0.19/ 1.12±0.17 cm/s for four-fold acceleration.

Discussion

Though the clinical feasibility of the proposed scheme was shown on one PAD patient, the effectiveness of magnitude regularization may be degraded depending on the flow pattern in the diseased vasculature. For instance, if arterial blood spins in turbulent or vortex flow exhibit significant phase dispersion within a voxel, the net magnitude of each voxel may significantly differ depending on the amount of dephasing as determined by the applied bipolar gradient. Further investigation on this effect would be warranted on a cohort of vascular patients.

Conclusion

The proposed magnitude regularization utilizes the magnitude similarity among different bipolar encoded data, and has shown to improve reconstruction accuracy as demonstrated by healthy and patient subject studies. The performance of the proposed technique in cases of arterial pathology needs to be further investigated.

Acknowledgements

This work has been supported by NRF-2019R1F1A1058872 and NIH R01 HL135500.