Introduction

Maxwell correction is a well-established technique to correct for phase offset errors in phase-contrast (PC) flow MRI induced by concomitant magnetic gradient fields¹. While often negligible at high magnetic fields (3T) the influence of Maxwell terms increases for higher gradient strengths, off-center applications and fast pulse sequences. For real-time PC flow MRI based on highly undersampled radial FLASH and model-based reconstructions^2,3 Maxwell terms have been neglected so far. This work therefore proposes to include a spoke-wise Maxwell correction into the model-based PC reconstruction framework² and demonstrates its importance for multi-directional real-time PC flow MRI at the aortic arch³.

Methods

Maxwell terms as described in¹ are calculated in the pulse sequence³ for each encoding step and individual k-space line. The model-based PC reconstruction² jointly estimates the image $$$\rho$$$, a phase difference map $$$\Delta\phi$$$, and the coil profiles $$$c_j$$$ by nonlinear inversion. The original forward model is formulated as: $$Y_{j,l}=P_l\;F\;\{\;\rho\cdot\exp(\,i\;\Delta\phi\;S_l\,)\cdot c_j\;\},\;\;\;\;\;\;\;\;\;S_l=\{0,1\}$$
Here $$$Y_{j,l}$$$ denotes the radial raw data of the $$$j$$$-th coil element and the $$$l$$$-th encoding step after gridding onto a Cartesian grid. The Fourier transformation is indicated by $$$F$$$ and $$$P_l$$$ describes the sampling pattern (s. Fig. 1). In standard Cartesian sampling the Maxwell terms are constant over different k-space lines and therefore can be derived from the gradient waveforms of one single (central) k-space line. For radial imaging, however, the Maxwell terms may vary for different lines (spokes) as the gradient waveforms change from spoke to spoke. This has to be considered when including the Maxwell phase contributions into the model:
$$Y_{j,l}=\sum_s^{N_s}P_{l,s}\;F\;\{\;\rho\cdot\exp(\,i\,\Delta\phi\;S_l\;+\;i\,M_{l,s}\,)\cdot c_j\;\}$$
As depicted in Figure 1, the sampling pattern is split up into individual patterns for each spoke to account for spoke-dependent Maxwell terms $$$M_{l,s}$$$. Note that the number of Fourier transformations also increases by the number of spokes $$$N_s$$$. As a compromise without additional Fourier transformations, a frame-wise correction can be performed using spoke-averaged Maxwell terms:
$$Y_{j,l}=P_{l}\;F\;\{\;\rho\cdot\exp(\,i\,\Delta\phi\;S_l\,)\cdot\bar{\mu_l}\cdot c_j\;\},\;\;\;\;\;\;\;\;\;\bar{\mu_l}=\frac{1}{N_s}\sum_s^{N_s}\exp(\,i\,M_{l,s}\,)$$
Three-directional PC flow MRI of the human aortic arch was performed on a 3 T MRI system (Prisma, Siemens Healthcare, Erlangen, Germany). Sequence and acquisition scheme were taken from³, however, with small modifications for faster timing: TR/TE=2.77 ms/1.92 ms, flip angle 10°, in-plane resolution 1.8 mm, slice thickness 6 mm, FOV 320 mm, VENC=200 cm s^-1, 4 x 5 radial spokes. The achievable measuring time per dataset was 55 ms corresponding to 18 fps. Model-based reconstructions were performed without Maxwell correction as well as with frame-wise and spoke-wise Maxwell correction

Results

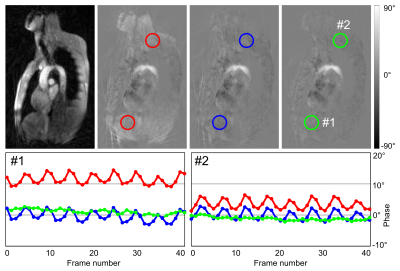
Figure 2 summarizes the advantage of the proposed Maxwell correction by showing PC velocity maps without, with frame-wise and with spoke-wise Maxwell correction, respectively. Visual inspection and ROI evaluation reveal a strong influence of concomitant fields expressed in phase offsets in areas of static tissue. In accordance to the theory of concomitant fields these offsets increase when moving to outer image regions (away from the iso-center). The frame-wise correction successfully suppresses the phase errors. While residual image artifacts and temporal fluctuations of quantitative velocity values are still present, the spoke-wise Maxwell correction eliminates both artifacts and fluctuations. The spoke-wise approach best describes the underlying physics and for the given example significantly improves the image quality.
Figure 3 shows the phase offset maps for the three encoded velocity directions and five different spokes per frame. Significant phase contributions for individual spokes lead to large inter-spoke differences - especially in the AP flow direction. This finding explains the necessity for a spoke-wise Maxwell correction. For the through-plane flow encoding a frame-wise correction was found to be sufficient (not shown) which is reflected in similar offset maps for different spokes. Velocity encoding along the B0 field (FH direction) revealed the lowest phase offsets and little to no differences were observed in Maxwell-corrected reconstructions.

Discussion

Although the effects of Maxwell terms can often be ignored at 3 T and conventional through-plane flow MRI studies, this work gives an example where the Maxwell correction is indispensable: Using a timing-optimized radial sequence with flow encoding in multiple directions³ the concomitant field contributions can result in significant phase offsets. Though at the expense of additional computation time, the proposed Maxwell correction successfully eliminates these unwanted phase contributions. The method can be integrated for online use and therefore better suits the requirements for real-time imaging than an offset correction by background fitting in a post-processing step. The impact of Maxwell terms and the need for correction is expected to be of even higher relevance in the low flow regime, e.g. CSF flow measurements, with high flow-encoding gradient moments.

Conclusion

For real-time PC flow MRI with flow-encoding gradients in arbitrary directions, Maxwell terms can be of significant magnitude and have to be corrected. For undersampled radial imaging, the Maxwell correction is best performed using a spoke-by-spoke approach which has successfully been integrated into a model-based reconstruction technique for PC flow MRI.

Acknowledgements

No acknowledgement found.