Introduction

Diabetic cardiomyopathy is characterised by a long latent phase, believed to be driven by myocardial metabolic dysregulation, before the development of diastolic and later systolic dysfunction. 31P MRS is able to quantify phosphotransfer in the heart, namely the first-order rates of the phosphocreatine-adenosine triphosphate reaction$$\text{PCr}\underset{k_r}{\stackrel{k_f}{\rightleftharpoons}}\text{ATP}\underset{k_f'}{\stackrel{k_r'}{\rightleftharpoons}}\text{ADP}+\text{Pi}.$$


The saturation of ATP followed by the simultaneous saturation of PCr and Pi for varying durations permit the determination of the total forward and reverse flux of ATP, by fitting acquired concentrations to the time-integrated solutions of the Bloch-McConnell equations for longitudinal magnetisation $$$M_z(t)$$$:[1]
$$\frac{\partial}{\partial{}t}\begin{pmatrix}M_{z}^\text{PCr}\\M_{z}^\text{ATP}\\M_{z}^\text{Pi}\end{pmatrix}=\begin{pmatrix}\frac{1}{T_{1}^\text{PCr}}&0&0\\0&\frac{1}{T_{1}^\text{ATP}}&0\\0&0&\frac{1}{T_{1}^\text{Pi}}\end{pmatrix}\begin{pmatrix}M_{0}^\text{PCr}-M_{z}^\text{PCr}\\M_{0}^\text{ATP}-M_{z}^\text{ATP}\\M_{0}^\text{Pi}-M_{z}^\text{Pi}\end{pmatrix}+\begin{pmatrix}-k_f&k_r&0\\k_f&-(k_r+k_r')&k_f'\\0&k_r'&-k_f'\\\end{pmatrix}\begin{pmatrix}M_{z}^\text{PCr}\\M_{z}^\text{ATP}\\M_{z}^\text{Pi}\end{pmatrix}$$

This approach is challenging at ultrahigh-field due to the long pulse requirements compared to T2; B1 inhomogeneity; and difficulty in ensuring uniform and flat saturation of only the desired resonances. This work presents the novel use of quasi-adiabatic optimised saturation pulses, designed using Optimal Control theory, to this problem.

Methods

Experimental design: Wistar rats fed high-fat diet and given a low (15-25mg/kg) streptozotocin dose were used as a model of hyperglycaemic, hypoinsulinaemic Type-2 Diabetes with known cardiometabolic abnormalities (n=12; n=10 controls).[2]

Rats were sacrificed via anaesthetic overdose, and hearts rapidly arrested in ice-cold Krebs-Henseleit buffer, containing 1.2mM KH2PO4 to prevent the loss of intracellular phosphate. The heart was weighed, and the aorta cannulated prior to Langendorff-mode perfusion with Krebs-Henseleit buffer at 37ºC. A balloon containing 100mM phenyl-phosphoric acid (PPA) was introduced into the left ventricle, and inflated to achieve an end-diastolic pressure between 3-5mmHg.

MR Protocol: Fully-relaxed pulse/acquire spectroscopy (TR=10s, 32 averages, 90º flip angle, 10 kHz BW, 2048 points) was used for absolute quantification on the basis of the LV PPA balloon, its volume, and the weight of the heart, using a 20 mm dual-tuned 1H/31P volume coil at 12T. A progressive-saturation experiment was then performed (on $$$\gamma$$$-ATP, $$$T_\text{sat}=[0,\,0.36,\,0.6,\,1.2,\,2.4,\,4.8]\,s$$$) prior to dual-band (PCr+Pi) progressive-saturation.

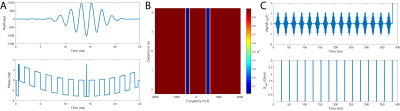
For dual-band saturation, a time-domain optimal-control algorithm proposed for the equivalent problem of optimising simultaneous-multi-slice profiles[3] was modified&used. Spectral flatness between saturation bands was encoded in the optimisation framework. A different approach was used to promote adiabacity. The SLR algorithm can design adiabatic pulses if a phase term varying quadratically with frequency is imposed on the desired spectral profile $$F(\omega) = F_0(\omega) e^{ik\omega^2}.$$ From this, the corresponding coefficients $$$b$$$ of the $$$\beta(z)$$$ polynomial can be calculated (as $$$b=\mathcal{FT}(F(\omega))$$$) and a least-phase $$$\alpha(z)$$$ polynomial computed.[4] This gives $$$B_1(t) = \mathcal{SLR}^{-1}(\alpha(z), \beta(z))$$$. Therefore, computationally quickly, a slowly-varying quadratic phase term was imposed into the saturation pulse in the optimal-control framework (Fig.$$$\,$$$1A).

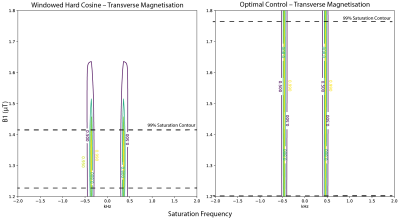
This resulted in a 25ms long dual-band pulse with a 950Hz gap between saturation bands, a 150Hz FWHM of each pole, and a maximum $$$(1-10^{-5})$$$% excitation between the bands (Fig.$$$\,$$$1B). Other spectral parameters were as above. A $$$>2.5$$$-fold improvement in B1-insensitivity was observed compared to a hard-cosine pulse (Fig.$$$\,$$$2). This represents the novel development of a multi-frequency-selective quasi-adiabatic RF pulse. The corresponding single-band saturation pulse was designed via optimal-control with quadratic phase modulation. A SNEEZE pulse provided as an initial condition, and the optimised pulse had a 150 Hz bandwidth, and a $$$<10^{-5}$$$% ripple(Fig.$$$\,$$$1C).

Results

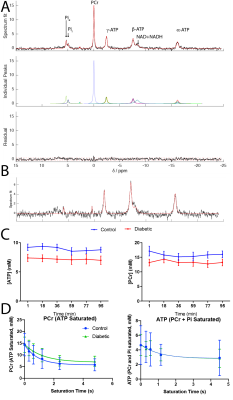
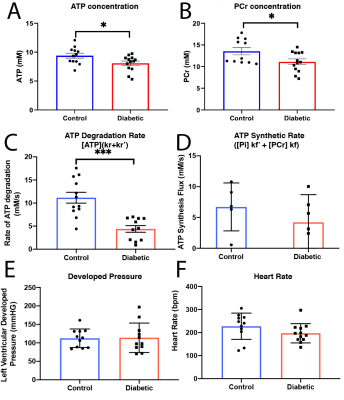
High SNR data were obtained (Fig.$$$\,$$$3A, B) and quantified with AMARES[5]. PCr and ATP were constant over the duration of the experiment (Fig.$$$\,$$$3C). Once quantified, data were fit via Levenberg-Marquardt to the time-integrated solutions of Eq.(1)(Fig.$$$\,$$$3D). Data presented are mean±SD. Unpaired, unequal-variance $$$t$$$-tests were performed.

Diabetes reduced [ATP] (from 9.3mM to 7.78mM, $$$p<0.05$$$) and [PCr] (from 13.53mM to 11.12mM,$$$\,p<0.05$$$) (Fig.$$$\,$$$4A, B), but there was no significant reduction in the PCr/ATP ratio. However, the rate of ATP degradation was significantly reduced (from 1.2 to 0.563s$$$^{-1}$$$) in diabetes (Fig. 4C). No functional changes occured, consistent with the clinical presentation of a long "latent" phase of diabetic cardiomyopathy (Fig. 4E,F).

Discussion and Conclusion

The diabetic heart is metabolically impaired, with a reduction in [PCr] and [ATP] compared to controls. The use of a quasi-adiabatic, extremely flat dual-band saturation scheme permits the quantification of the total rate of ATP degradation, significantly reduced in diabetes while cardiac function was unchanged.

The reduction in both [PCr] and [ATP] was observed in the absence of a statistically significant decrease in the PCr/ATP ratio, the most commonly used clinical marker for cardiac energetic dysfunction. It has previously been observed in (human) dilated cardiomyopathy that the absolute concentration of both [PCr] and [ATP] may show a stronger correlation with cardiac function than PCr/ATP.[6] Although a significant reduction in PCr/ATP was reported in obese T2DM patients[7], its potentially variable sensitivity to disease may be explained by the separate decrease of [PCr] and [ATP] as shown in this study. Others have shown that cardiac CK flux is not decreased in rat models of T2DM,[8] therefore the reduction in ATP degradation is likely to be caused by a reduction in the $$$k_r'$$$ term. We note that the mean rate constant of degradation in the control heart, 1.19±0.15, agrees quantitatively with that determined by Spencer et al.[1] (1.15±0.19) This study is consistent with the hypothesis that metabolic changes occur before functional ones, and drive the slow but steady decline into failure. Given the reliance of diabetic myocardium upon fatty acid oxidation, it hints that alterations may exist, e.g. the mitochondrial aceyl/acetyl-CoA mediated import of fatty acid for ATP production