Introduction

Machine learning techniques enable new ways of harvesting information from large patient databases that can be used to extract global features, personalized features of specific subjects’ subgroups, or even one single individual. One relevant application consists in learning atlas-like anatomical characteristics from large databases and use this knowledge to provide a personalized “healthy version” of the anatomy of a specific subject. Conceptually, by emphasizing the differences between the expected “learned” subjective anatomy and the real "acquired" anatomy, it is possible to detect morphological anomalies. Here, we test the feasibility of a) learning at least a subset of cardiac anatomical features from a database of cardiac MRI scans, and b) whether we can use this atlas-like knowledge to generate inpainted anatomical details that match the surrounding anatomy.

Methods

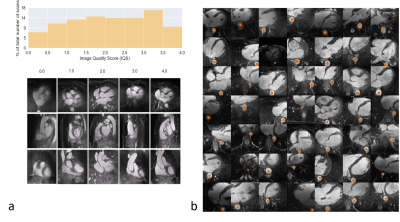
Input Data. N=1145 3D whole-heart datasets with high isotropic spatial resolution (0.9 – 1.1mm)³ were collected between 2015 and 2018 using a prototype respiratory self-navigated sequence^1,2 on a 1.5T clinical MRI scanner (MAGNETOM Aera, Siemens Healthcare, Erlangen, Germany). All datasets were automatically graded for general image quality³ (Figure 1a) and 297 volumes with grade >3 (out of 4 on a Likert scale) were selected. A semi-automated segmentation algorithm could extract a variable number of 2D patches of 128x128 pixels that contained part of the descending aorta (orange dots, Figure 1b). 80% of the data (237 volumes) were used for training and 20% for testing.
Networks. A generative adversarial network (GAN) architecture⁴, consisting of two communicating networks: a critic and a generator, was chosen. While the critic needs to differentiate between real and generated images (e.g. by grading them on a certain distance function), the generator tries to “fool” the critic by producing images that result in critic scores that are similar to those assigned to the training images. Both networks are based on a deep convolutional architecture with one input layer, six hidden layers, and one output layer. The input of the generator was a random 100-dimensional vector ($$$z\tilde{}Ν(0,1)$$$). The input of the critic consisted of batches with 49 2D images each.
Patch generation. A Wasserstein GAN⁵ with a gradient penalty term (WGAN-GP) [6] was used as a loss function (L) as described below:
$$L=\underset{\tilde{x}\tilde{}\mathbb{P}_g}{\mathbb{E}}[D(\tilde{x})]-\underset{x\tilde{}\mathbb{P}_r}{\mathbb{E}}[D(x)]λ\cdot\underset{\hat{x}\tilde{}\mathbb{P}_{\hat{x}}}{\mathbb{E}} [(‖∇_{\hat{x}}D(\hat{x})‖_2-1)^2]$$ $$\hat{x}=t\tilde{x}+(1-t)x,\qquad0≤t≤1$$
Where $$$x$$$ belongs to the distribution of real images, $$$\tilde{x}=G(z)$$$ belongs to the generated images, and $$$\hat{x}$$$ is sampled from both distributions. The regularization term penalizes the model if the gradient of the critic moves away from 1. This has been proven to increase the training stability without the need of hyperparameter finetuning.
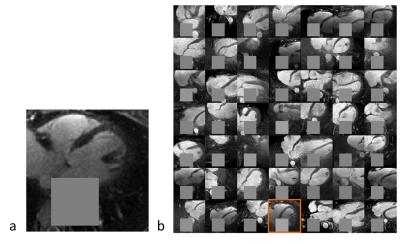
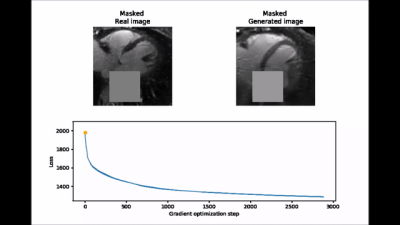
Inpainting approach. Subsequently, an inpainting framework consisting of three steps was developed around the WGAN-GP. First, a mask $$$(M)$$$ of 25x25 pixels is placed onto one of the 2D patches from the test set $$$(y)$$$ to exclude the aorta. Second, the same mask is applied to a generated image produced by the WGAN-GP network $$$(G(z))$$$. Third, the closest latent space representation of the masked real image $$$(M\circ{}y)$$$ is found by applying gradient descent on the masked synthetic image $$$(M\circ{}G(z))$$$. The loss function for the gradient descent operation is an empirical balance between contextual loss (the masked version of the final image needs to resemble its real counterpart) and perceptual loss (the final image needs to look real based on the critic score)⁷.
$$L(z)=L_{contextual}(z)+λ\cdot{}L_{perceptual}(z)=‖M\circ{}G(z)-M\circ{}y‖-λ\cdot{}D(G(z))$$
To improve convergence towards a global minimum, the initial guess must be already close to the real masked image. This was achieved by choosing among 20 different initialization vectors the image with lowest initial loss function value.
Data Analysis. At this stage, careful visual inspection of the generated patches compared to those used for training, performed by an expert in cardiac MRI (D.P. 10 years of experience), was considered as a qualitative metric for the feasibility of the patch generation. A qualitative stability analysis was performed for the inpainting part by visually assessing the differences in position and perimeter of the generated portion of the inpainted aorta starting from different initialization.

Results

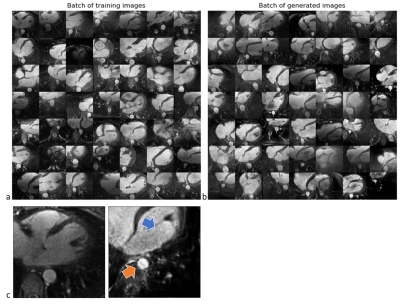
Figure 2 shows two batches of 2D patches side by side, with the real and generated images on the left and right side, respectively. Overall, the appearance of the generated images corresponds well to realistic cardiac anatomies, confirming that the training process was successful. However, at closer inspection, a residual overall “patchiness” as well as some structured noise pattern show that some improvement is needed. The inpainting approach allowed generating visually realistic versions of the masked aorta in a subset of the test set (Figure 3), when comparing to the original image (a), starting from the patch with the lowest initial cost function value (b), and performing gradient descent (Figure 4). Although the inpainted anatomy is variable (e.g. position and diameter of the aorta) and highly dependent on the initial guess (Figure 5), these preliminary results are encouraging.

Discussion and Conclusion

We demonstrated the feasibility of learning the complexity of the heart from a database of MR images using a GAN. This network can also be potentially used to generate realistic anatomical details using inpainting. A systematic optimization and a quantitative comparison between the real images and generated patches as well as between real anatomy and inpainted anatomy is warranted.

Acknowledgements

No acknowledgement found.