2217

An MR image-guided left-ventricular shape model embedding local physiological coordinates and directions

Stefano Buoso¹, Christian T Stoeck¹, Johanna Stimm¹, and Sebastian Kozerke¹
¹Institute for Biomedical Engineering, ETH Zurich, Zurich, Switzerland

Synopsis

We show the feasibility of embedding physiological coordinates and directions into a left ventricle anatomical shape model using Proper Orthogonal Decomposition. The volumetric anatomical mesh and the physiological parametrization can be personalized directly from the selection of control points on MR cardiac images. This approach provides a consistent way of augmenting low-resolution data using features from high-resolution datasets. Additionally, the physiological parametrization is automatically adapted to each specific case without any additional calculation steps. This simplifies the processing of clinical images and, particularly, strain calculations and microstructural analysis that require the definition of the physiological parametrization.

Introduction

The calculation of localized metrics, such as cardiac strains¹and myofiber directions², from cardiac MR data requires the definition of local physiological parametrization (PP). We propose to use a shape model embedding physiological coordinates and local coordinate systems to define a PP on the anatomy of interest. The model is generated from left-ventricular (LV) anatomy data obtained from high resolution images^3-5 and processed with dimensionality reduction algorithms⁶. The shape model is associated with a set of control points that are used to adapt it to the actual anatomy and automatically provide a consistent PP. Such an approach is relevant for processing clinical MR images with limited spatial resolution as it allows to augment low-resolution data with anatomical features of a high-resolution model including shape-adapted physiological coordinates and directions to facilitate the calculation of strain and directional diffusion metrics.

Methods

A reference mesh is generated from an idealized truncated ellipsoid with long axes dimensions of 120.0 mm and 140.0 mm (endocardium and epicardium), and short axes dimension of 60.0 mm and 80.0 mm (endocardium and epicardium). The distance from apex to base was set to 75.0 mm. The shape was generated in Abaqus⁷ and meshed using 27806 tetrahedral linear elements (6066 nodes). We considered 38 out of the 40 segmented masks available from the Whole Atlas Cardiac Model (WACM) dataset^3-5, of which we segmented the left ventricle from the apex up to below the left ventricular outflow tract, where we cut the anatomy with a plane parallel to the mitral valve. All shapes are oriented such that the center of the mitral valve coincides with the origin of the coordinate system, the outward mitral valve normal is parallel to the z axis and the anterior intersection of left and right ventricle is on the negative x axis. The shape-adapted physiological parametrization (PP) is defined in terms of transmural, longitudinal and circumferential coordinates, which approximate the prolate ellipsoid coordinate system⁸ by solving a linear diffusion problem with appropriate Dirichlet Boundary conditions⁹. Three diffusion problems are solved to define the local transmural, longitudinal and circumferential directions. The PP coordinates for each anatomy and the reference ellipsoid provide a mapping between each other. Consequently, the ellipsoidal mesh is registered into each of the segmented anatomies. Proper Orthogonal Decomposition (POD) is used to obtain the mean shape and a set of modes which minimize the reconstruction error of both anatomy and PP in a least square sense⁶. The Discrete Empirical Interpolation Method (DEIM)⁶ is used to identify the optimal set of boundary points that can be used in a constrained minimization problem to fit the amplitudes of the modes for the reconstruction.

Results

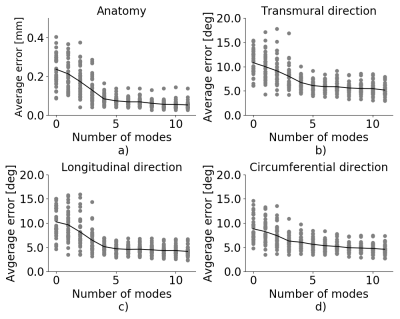
Fig. 1 show the mean shape with physiological coordinates and directions. The longitudinal coordinate (Fig.1a) ranges from 0 at the apex to 1 at the base of the ventricle, the circumferential coordinate (Fig.1c) starts from 0, at the anterior left-right ventricle intersection, and increases to 1 in counterclockwise direction, the transmural coordinate (Fig.1e) extends from 0 at endocardium to 1 at epicardium. Fig.1g shows the boundary points computed with DEIM that are used to calculate the amplitude of the corresponding POD modes. Only the first 11 points are shown for clarity. Fig.2 shows the effect of the superposition of the mean with the maximum and minimum contribution for the first 6 modes in long-axis and short-axis views. For each panel, only the corresponding mode has been considered, while the contribution of all other modes is set to zero. Fig.3 shows the reconstruction error of the WACM dataset for different number of modes used during the reconstruction. The error curve drops to 0.08mm/6.7°/5.2°/6.0° for anatomy, transmural direction, longitudinal direction and circumferential direction using the first four modes and flattens for higher modes. In Fig.4 the shape model (with 11 modes) has been fitted to the anatomy of one case from the ACDC dataset¹⁰ that has not been used in the computation of the shape model directly from the image.

Discussion

This work has demonstrated that it is possible to embed local physiological parameterization into a shape model that can be directly reconstructed when adapting a volume mesh to the anatomy in the image. The first 4 modes can already capture most than 99% of the global variability of the left-ventricular shape and its PP of the WACM dataset. The weights of the modes can be obtained from the sampling of control points on the boundary of the LV directly form the image, avoiding the need of registering an atlas on the mask to identify their location^6,8,11 Although we only considered 38 cases for the generation of the model, we can obtain satisfactory performance for data from an external dataset, demonstrating the feasibility of the approach.

Acknowledgements

This work has been partially supported by the Swiss National Science Foundation (PZ00P2_174144).

References

1. von Deuster C, Sammut E, Asner L, et al. Studying Dynamic Myofiber Aggregate Reorientation in Dilated Cardiomyopathy Using In Vivo Magnetic Resonance Diffusion Tensor Imaging. Circulation: Cardiovascular Imaging; 2016; 9(10).

2. Stoeck CT, von Deuster C, Genet M, et al. Second‐order motion‐compensated spin echo diffusion tensor imaging of the human heart. Magnetic Resonance in Medicine; 2016; 75:1669-1676.

3. Zhuang X and Shen J. Multi-scale patch and multi-modality atlases for whole heart segmentation of MRI, Medical Image Analysis; 2016; 31:77-87.

4. Zhuang X. Challenges and Methodologies of Fully Automatic Whole Heart Segmentation: A Review. Journal of Healthcare Engineering; 2013; 4(3): 371–407.

5. Zhuang X, Rhode K, Razavi R, et al. A Registration-Based Propagation Framework for Automatic Whole Heart Segmentation of Cardiac MRI. IEEE Transactions on Medical Imaging; 2010; 29(9):1612-1625.

6. Buoso S, Manzoni A, Alkadhi H, et al. Reduced-order modeling of blood flow for noninvasive functional evaluation of coronary artery disease. Biomechanics and Modeling in Mechanobiology; 2019; 18(6):1867-1881.

7. Abaqus 2018, Analysis User’s Manual, 2018, Simulia, Dassault Systems.

8. Toussaint N, Stoeck CT, Schaeffter T , et al. In vivo human cardiac fibre architecture estimation using shape-based diffusion tensor processing. Medical Image Analysis; 2013; 17(8):1243-1255.

9. Doste R, Soto-Iglesias D, Bernardino G, et al. A Rule-Based Method to Model Myocardial Fiber Orientation for Simulating Ventricular Outflow Tract Arrhythmias. In: Pop M., Wright G. (eds) Functional Imaging and Modelling of the Heart. FIMH 2017. Lecture Notes in Computer Science, vol 10263. Springer, Cham.

10. Bernard O, Lalande A, Zotti C, Cervenansky F, et al. Deep Learning Techniques for Automatic MRI Cardiac Multi-structures Segmentation and Diagnosis: Is the Problem Solved? IEEE Transactions on Medical Imaging; 2018; 37(11):2514-2525.

11. Toussaint, N, Sermesant, M, Stoeck, C T et al. In vivo human 3D cardiac fibre architecture: reconstruction using curvilinear interpolation of diffusion tensor images. In: Jiang, T; et al. Medical Image Computing and Computer-Assisted Intervention - MICCAI 2010. 2010; 418-425.

Figures

Mean left ventricular shape with physiological parametrization: longitudinal position (a) and directions (b), circumferential position (c) and directions (d), transmural position (e) and direction (f). Panel g) shows the position of the control points resulting from the DEIM algorithm on the mean shape for the first 11 modes.

Long- and short-axis views of the POD basis of the shape model. Orange and blue shapes represent the effect of maximum and minimum amplitudes of the POD modes from the WACM dataset, respectively. Panels (a) to (f) show modes from 1 to 6.

Reconstruction errors of the WACM dataset as a function of the number of modes for (a) anatomy, (b) transmural direction, (c) longitudinal direction and (d) circumferential direction. Anatomical errors are defined as the norm of the distance between the real and reconstructed points, while directions errors are defined as the angle between the real and reconstructed directions. Scatter points represent the average error for each anatomy in the dataset, while the solid black line represents the mean.

(a) – (g) Overlay of original MR image and LV myocardium masks (orange) obtained from the shape model using 11 points. The amplitudes of the modes for reconstruction are calculated from the boundary points of DEIM selected directly on the image. (h) Reconstruction of circumferential (yellow) and longitudinal (orange) directions directly on the image.

Proc. Intl. Soc. Mag. Reson. Med. 28 (2020)

2217