Introduction

High-resolution CINE imaging of the heart is challenging due to long acquisition times, variable breathing patterns, and changing heart rates. These physiological variations lead to different image acquisition times for each distinctive cardio-respiratory motion state and consequently to differently filled k-spaces. Cartesian sampling is attractive for speed of image reconstruction, however if a standard linear ordered strategy is used large parts of the k-space will be missed for some cardio-respiratory states (images).

Retrospective schemes address this using spiral profile k-space trajectories with a golden-angle view ordering scheme(1–3). They provide a near uniform variable density k-space sampling in the presence of varying acquisition times and provide temporal incoherence for flexible image reconstruction. However these retrospective schemes repeatedly sample the same central k-space locations and sometimes peripheral k-space. New motion detection methods that rapidly detect the cardio-respiratory state using the RF coils can be used for prospective gating(4).

In this work, we consider a prospective k-space encoding strategy for free-breathing cardiac CINE with (i) pre-defined k-space sampling tables for each cardio-respiratory state, (ii) temporal-incoherence and variable density masks with a randomised k-space traversal order, and (iii) minimisation of eddycurrents associated with rapid changing phase encoding(5), by segmenting k-space into clusters. We have termed this method CLustered, randomly Ordered Cartesian K-space (CLOCK). We compare CLOCK to a retrospective method with tiny golden-angle view ordering (CASPR-tiger)(2) in simulations.

Methods

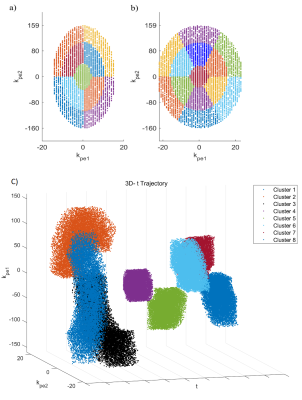
CLOCK algorithm: For each of 300 cardio-respiratory states (30 cardiac and 10 respiratory), a Poisson-disk variable density sampling mask is created(6) with a fully sampled central region. Each mask is subdivided into Nc clusters, each with the same number of samples per cluster (Ns). These clusters are arranged on concentric rings. For 3D imaging each cluster has a pie-like shape and an equal central angle. A maximum of six clusters per ring are used and multiple rings were created to accommodate a larger matrix sizes, this is shown in figure 1. The temporal order within each cluster is randomised, with the exception of the central 5x5 samples of k-space that are placed at the beginning of the cluster to increase the probability of measuring them.

During the scan the current phase encoding is looked up in a table by incrementing the table index for the current cardio-respiratory state and cluster (from 1 to Ns). When any one cardio-respiratory state reaches Ns samples the next cluster is selected for all states. The scan is complete when all clusters are complete in any one state.

Using previously recorded cardio-respiratory motion signals from five subjects(4) simulations were carried out in MatLab (MathWorks). A 3D cine was simulated with a phase-encoding matrix of 320x48 (PE1xPE2) and acceleration factors R=2 and R=4 for 3D-CLOCK with Nc=7 and also for a the retrospective method CASPR-Tiger(2), with a tiny golden-step of ), with N=10 elliptic rings and N=10 angular segments(2). Scan times for CASPR-Tiger were matched to the average scan time of CLOCK for each data set.

The maximum of the peak-to-side-lobe ratio (PSR) of the Point Spread Function (PSF) was calculated. In addition the ratio of the standard deviation of the side-lobes to the main-lobe of the PSF were calculated(7), termed incoherence ratio. Both increase with encoding quality.

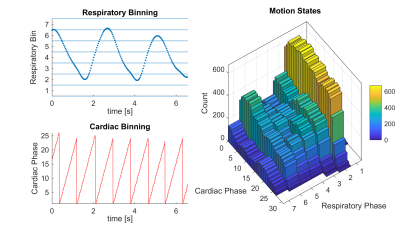
A volunteer was scanned at 7T (Siemens) with an 8‐channel, dipole parallel transmit (pTx) /receive coil (MR Coils) with a 3D thin-slab CINE GRE sequences (1.0×1.0×1.0 mm3; TR/TE = 4/1.57 ms), and FOV and matrix size of 320×320×48mm3, R = 2. The pTx scattering matrix was used to prospectively cardio-respiratory gate(4) with a 3 mm respiratory bin and 40 ms cardiac bin. BART toolbox(6) was used for image reconstruction.

Results

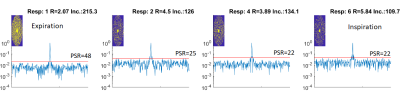
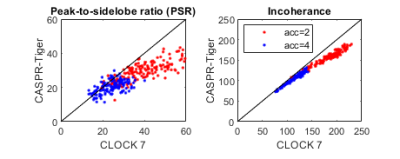
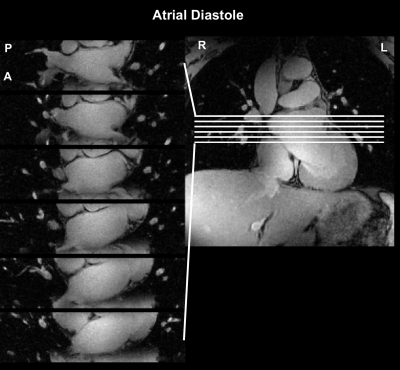
Data from one subject used in the simulations is shown in Figure 2 along with how often each cardio-respiratory state occurs. Figure 3 shows simulated CLOCK sampling patterns and PSF while Figure 4 plots the PSR and incoherence ratios of CLOCK against CASPER-Tiger for each cardiac phases of the end expiratory bin. On average the PSR is 38% higher for CLOCK with R = 2 and 22 % higher with R=4. The average efficiency for CASPER-Tiger was 83% and 90 % of that for CLOCK with matched durations for R =2 and R=4 respectively. A frame from the 7T in-vivo 3D CINE is shown in figure 5.

Discussion

The prospective method had higher efficiency which was markedly higher for the lower acceleration rate, this can be expected because as acceleration rates increase the retrospective methods probability of resampling decreases (with the exception of the centre of k-space). The incoherence ratio improved when using CLOCK roughly in line with the improved efficiency. What was unexpected was that the PSR improved more than twice as much as the efficiency did when using CLOCK for both targeted acceleration rates. This is likely due to the Poisson-Disk under sampling masks used in CLOCK, which produce preferable side lobe properties. This may be beneficial for compressed sensing image reconstruction. The improved acquisition efficiency and PSF can be used for faster acquisition times while maintaining or improving image quality.

Conclusion

The proposed prospective encoding strategy for 3D Cartesian CINE improves acquisition efficiency and enables a controlled under-sampling mask.

Acknowledgements

This work was supported by funding from the Engineering and Physical Sciences Research Council (EPSRC) and Medical Research Council (MRC) [grant number EP/L016052/1], the Clarendon Fund and Keble College de Breyne Scholarship. AH thanks the British Heart Foundation centre of research excellence (Oxford).