2140
Wave-balanced Steady State Free Precession (Wave-bSSFP) for free breathing cardiac MR angiography1IHU LIRYC, Fondation Bordeaux Université, Pessac, France, 2U1045 CRCTB, Université de Bordeaux, Bordeaux, France, 3INSERM, CRCTB, U1045, Bordeaux, France
Synopsis
Using Wave-CAIPI-like techniques to accelerate Balanced Steady-state Free Precession (bSSFP) sequences is a new parallel imaging technique that reduces the noise levels on the reconstructed image compared to conventional parallel imaging. On the heart, this combination of sequence has not been tested. The experiments show that the movements of the thorax are not an issue, as long as a respiratory and ECG triggering are employed. A retrospective acceleration of 5.4 on a sheep heart image with a 1.4mm isotropic resolution has been achieved.
INTRODUCTION
3D acquisitions in the heart are time consuming due to the necessity to trigger the acquisition on the heart rate and compensate the respiratory motion. In clinical settings a trade-off between acquisition duration and spatial coverage is often compulsory. Parallel-imaging techniques allow reducing the acquisition time while producing good quality images by taking benefits of array receivers1. More recently, Wave-CAIPI acquisitions initially proposed for whole brain imaging have shown the added value of adding sinusoidal gradients during readout to better control aliasing2. Su and al have shown the effectiveness of using a modified Wave-CAIPI technique conjointly with a bSSFP sequence (Wave-bSSFP) in reducing the g-factor when high acceleration factors are employed3. While this holds true for the brain, the feasibility of such a technique on the heart remains to be evaluated. First, coil coverage surrounding the heart remains less optimal as compared to whole-brain coil arrays. In addition, issues might be related to cardiac and respiratory motions, together with the presence of structures showing different magnetic susceptibilities inside the thorax. In this work, we implemented a wave-bSSFP sequence with T2-preparation module for in vivo 3D rapid cardiac imaging.METHODS
- Pulse Sequence: We implemented at 1.5T (MAGNETOM Aera, Siemens Healthineers) a wave encoded b-SSFP sequence with a 40 ms T2-preparation module. Wave gradients were truncated (as proposed by Su and al) to maintain the balanced gradient condition3. Wave gradients intensity was set up to 4mT/m. The acquisitions were ECG gated in cardiac diastole and a crossed pair navigator echo was used to track and compensate respiratory motion (4 mm acceptance window). A flip angle ramp up over 10 TR was used to reach the steady state. Trajectories for the PSF estimation were measured using 1D calibration scans prior to image acquisition4. Trajectories calibration consisted in acquiring two 2 mm slices in the y direction and two 2 mm slices in the z direction. During these acquisition, only the gradient to characterize were played. The phase on the MRI signal was analyzed to retrieve the trajectory. The chronogram of the sequence is shown in Figure 1.
- In Vivo Experiment: Fully sampled acquisitions were performed in the thorax of an anesthetized sheep (protocol approved by ethic committee) with the following parameters: TE=2ms; TR=350ms; Flip Angle = 90°; 50 segments acquired per cardiac beat; FOV=300x300x112mm3 and matrix size=208x208x80 resulting in an isotropic spatial resolution of 1.4 mm. Acquisition were oversampled 8 folds on the readout direction. We used 40 coil elements (body and spine multi-array coils). Calibrations and imaging data were streamed inline to the Gadgetron framework5 and a MATLAB (MATLAB 9.5, The Mathworks, Inc) script using BART toolbox6 was run for image reconstruction.
- Offline Image Reconstruction: The fully sampled in-vivo acquisition was reconstructed to create a reference 3D volume. The effect of the wave gradient was de-convoluted from the fully sampled data using the PSF formalism developed by Bilgic and al2: $$\small\begin{equation}wave[x,y,z] = F_x^{-1}(PSF[k_x,y,z]\times F_x.m[x,y,z])\end{equation}$$ where $$$\small\begin{equation}m[x,y,z]\end{equation}$$$ is the underlying magnetisation, $$$\small\begin{equation}wave[x,y,z]\end{equation}$$$ is the image convoluted by the wave gradients and $$$\small\begin{equation}F_x\end{equation}$$$ is the Fourier transform operator on the x axis. The corresponding images served as a gold standard. The raw data were then retrospectively subsampled and reconstructed to simulate accelerated acquisitions. For this, a Poisson undersampling mask was applied in ky-kz dimensions. Coils Sensitivities Maps were estimated using ESPIRIT1 on autocalibration scans (ACS kernel size = 24x24 pixels) or on low-resolution Wave-bSSFP images de-convoluted by low resolution PSFs (kernel size=24x24 pixels)7. The images were afterwards reconstructed using general ESPIRIT model proposed in BART toolbox.
RESULTS
During acquisition, the fully sampled dataset were acquired over 15 minutes, reconstructed online using our proposed Gadgetron/BART algorithm and transferred back to the scanner for immediate image visualization. The proposed sequence and reconstruction pipeline offer flexibility to tune parameters during the experiment.Figure 2a and b show the theoretical and experimental trajectories resulting from a wave gradients played along ky or kz directions respectively. Strong drifts are observed between experimental and theoretical trajectories mainly due to eddy currents and gradient imperfections. Using the theoretical trajectories ghosts are clearly visible (Figure 2c) as we move away from the scanner isocenter. With the proposed calibration scan, ghosts disappeared in the reconstructed image (Figure 2c).
Figure 3 shows images after 3.4 and 5.4 acceleration factors. Estimation of coil sensitivities using low-resolution deconvoluted data or ACS lines results in less than 0.2% of signal difference.
DISCUSSION
The results validate the use of a Wave-bSSFP type sequence on the heart. In a first approach, data subsampling was performed offline to offer flexibility in image reconstruction.Images show acceptable RMSE compared to the fully sampled data at both 3.9 and 5.4 acceleration factors. Data with higher accelerations factors are currently being investigated upon. Incorporating Compressed Sensing in the SENSE reconstruction model should result in an improvement of the image quality.
CONCLUSION
This work presents the first usage of a Wave-CAIPI type sequence on the heart using a bSSFP sequence. Similar image qualities were obtained after subsampling the full k-space by a 3.9 and 5.4 factor showing that 3D acquisition of the heart with a 1.4 isotropic spatial resolution is feasible much faster with good image quality.Acknowledgements
This work received financial support from the French National Investments for the Future Programs: ANR-10-IAHU-04 (IHU Liryc)References
1. Uecker M, Lai P, Murphy MJ, et al. ESPIRiT-an eigenvalue approach to autocalibrating parallel MRI: Where SENSE meets GRAPPA. Magnetic Resonance in Medicine. 2014;71(3):990-1001.
2. Bilgic B, Gagoski BA, Cauley SF, et al. Wave-CAIPI for highly accelerated 3D imaging. Magnetic Resonance in Medicine. 2015;73(6):2152-2162.
3. Su S, Liang D, Qiu Z, et al. Accelerating Three-Dimension Balanced Steady-State Free Precession Imaging with Modified Wave-CAIPI Technique. Annual Meeting ISMRM, Montreal 2019, In Proc. Intl. Soc. Mag. Reson. Med. 27
4. Zhang Y, Hetherington HP, Stokely EM, Mason GF, Twieg DB. A novelk-space trajectory measurement technique. Magnetic Resonance in Medicine. 1998;39(6):999-1004.
5. Hansen MS, Sørensen TS. Gadgetron: An open source framework for medical image reconstruction: Gadgetron. Magn Reson Med. 2013;69(6):1768-1776.
6. Uecker M, Ong F, Tamir J, Bahri D, Virtue P, Cheng J, Zhang T, and Lustig M. Berkeley Advanced Reconstruction Toolbox. Annual Meeting ISMRM, Toronto 2015, In Proc. Intl. Soc. Mag. Reson. Med. 23:2486
7. Chen F, Zhang T, Cheng JY, Shi X, Pauly JM, Vasanawala SS. Autocalibrating motion-corrected wave-encoding for highly accelerated free-breathing abdominal MRI: Wave-Encoding for Free-Breathing Abdominal MRI. Magn Reson Med. 2017;78(5):1757-1766.
Figures
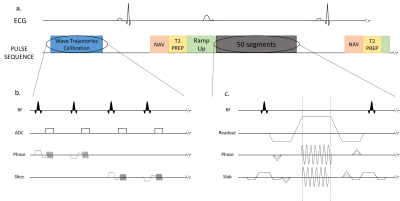
Figure 1. Sequences diagrams. Zoom in on the Trajectory Calibration Sequence (b.) and on the Wave-bSSFP sequence (c.).
(a.) During the acquisition, ECG and respiratory motion were recorded. The exam starts with a calibration module. The data was collected during diastole: first, a navigator scan, followed by a T2 Prep and a flip angle Ramp Up. Afterwards, 50 segments are acquired.
(c.) The wave encoding gradients are applied during the readout, in both phase and slab direction. The slab encoding wave gradient starts ¼ of a cycle after the phase wave gradient, and ends ¾ of a cycle earlier.
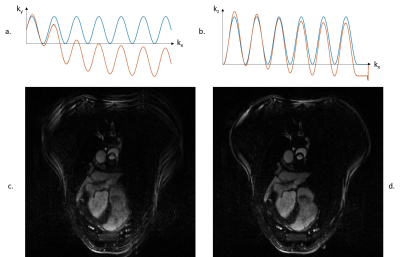
Figure 2.
(a.) and (b.) Theoretical (blue) and experimental (orange) trajectories resulting from the wave encoding.
(c.) Fully sampled image reconstructed using a PSF calculated with theoretical trajectories: ghosting artefacts visible.
(d.) Fully sampled image reconstructed using a PSF calculated with experimental trajectories: no ghosting artefacts.
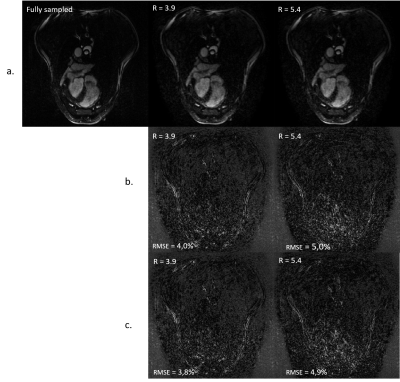
Figure 3.
(a.) Fully sampled reconstruction compared to 3.9-fold retrospectively accelerated and 5.4-fold retrospectively accelerated.
(b.) ESPIRIT coils sensitivities maps calculation carried on deconvoluted wave-bSSFP images. Relative error between the fully sampled and the accelerated data. Error was scaled up by five.
(c.) ESPIRIT coils sensitivities maps calculation was carried on autocalibration scans. Relative error between the fully sampled and the accelerated data. Error was scaled up by five.