Introduction

The modified Look-Locker inversion recovery (MOLLI) technique (1,2) is a T1 mapping technique widely used for cardiac applications. Its utility has also been extended to other organs, such as liver. However, when used in the organs (including the heart) sensitive to the respiratory motion, it requires a good breath-hold from patients for the accurate T1 quantification. Although the current total acquisition time of approximately 10~12 s is a reasonable breath-hold period for most patients, further reduction of total acquisition time—even if only a few seconds—would be crucial for some patients including pediatrics. With the current MOLLI signal modeling, the limiting factor for the time reduction is the use of the 3 parameter exponential modeling, which assumes the full recovery of longitudinal magnetization before the next inversion pulse. In this study, a new MOLLI signal modeling method without any restriction on the interval between inversion pulses is presented, and its validity is confirmed by applying it to the phantom-based MOLLI signals acquired with different acquisition timing schemes.

Methods

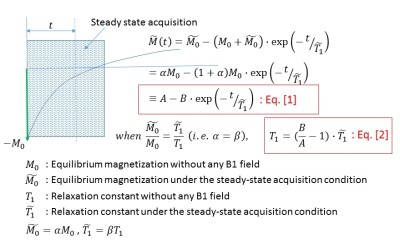
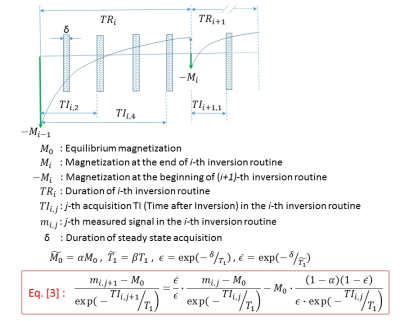
The conventional MOLLI signal modeling is based on the 3-parameter exponential modeling (Eq. [1] in Fig. 1), and the T1 is determined by the Eq. [2] in Fig. 1 (1,3). Here, $$M0-wave$$ and $$T1-wave$$ are used to represent, respectively, the equilibrium magnetization and T1 under the steady-state acquisition condition. The conventional MOLLI modeling can easily be derived when alpha=beta , as shown in the figure. The new modeling method is developed on a more realistic MOLLI acquisition case that is depicted in Fig. 2, where Eq. [3] shows the new modeling to describe the MOLLI signals acquired with the j-th TI (time after inversion) window after the i-th inversion pulse. With the new modeling, the unknown constants to determine would be 4-parameters (M-wave,T1-wave , alpha, and beta), but could be reduced to 3-parameters if, as conventionally assumed, alpha=beta . MRI measurements were done with a T1 phantom (consisting of 12 vials with different T1 values in the range from 200 ms to 2000 ms) in a clinical 1.5T MRI system (Philips, Netherlands). The MOLLI sequence (TR=1.9ms, TE=0.85ms, ETL=92) was run with a native (5s-3s-3s) or enhanced (4s-1s-3s-1s-2s) timing scheme. The reference T1 values of the phantom were also obtained by repeating an inversion recovery (IR)-based fast spin echo sequence (TR=6s, TE=19ms, ETL=11) while the inversion time was varied from 50ms to 5000ms. MOLLI signals were processed with a MATLAB routine developed according to the conventional modeling and the novel modeling presented here.

Results

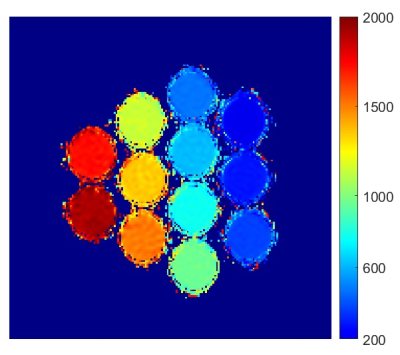
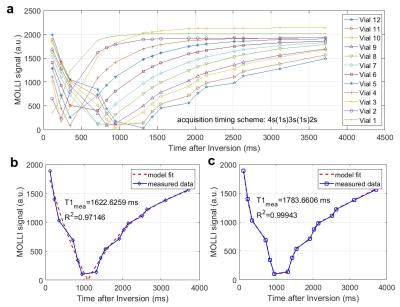
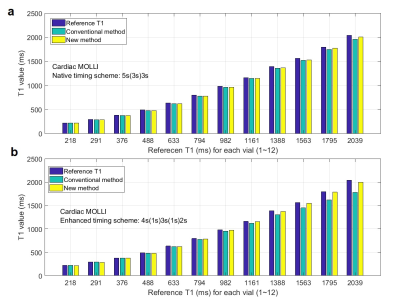
The T1 map of the T1 phantom used in this study was automatically generated by the MRI system, and is shown in Fig. 3. The vials were numbered from 1 to 12 in the order of their T1 values. The values of all vials from this map were equivalent to the conventionally obtained T1 values from the author’s MATLAB processing routine. The MOLLI signal changes of all vials for the enhanced timing scheme are shown in Fig. 4(a), where deviations from the traditional IR curve are shown toward the larger T1 vials. An example data set from vial 11 was processed by the conventional curve fitting, in Fig. 4(b), and by the novel 3-parameter curve fitting, in Fig. 4(c). The novel modeling strategy produced accurate T1 result and much better curve fitting. The discrepancy of measured T1 by the conventional MOLLI processing, especially in the case of the enhanced scheme, was much reduced by the new modeling approach, as shown in Fig. 5.

Discussion

As typically seen with the large T1 value in the case of the enhanced timing scheme, the deviations of measured signal from the traditional IR is due to the insufficient recovery before next inversion pulse. The new MOLLI processing strategy does not require full recovery of longitudinal magnetization before each inversion pulse, and any interval between inversion pulses is acceptable. As a result, the generally inserted resting period will be unnecessary. The improved T1 accuracy and MOLLI signal fitting in the case of enhanced timing scheme in this study suggests that the new modeling can be utilized to design a new acquisition timing scheme for a much shorter total acquisition time. Proposing specific shorter acquisition timing schemes will be in the topic of another study.

Conclusion

A new MOLLI signal processing strategy introduced here strongly suggests a possibility to design an improved acquisition timing scheme to further reduce the total MOLLI scan time (e.g. a few seconds less than 10 sec) by further reducing the interval between successive inversion pulses.

Acknowledgements

No acknowledgement found.