Introduction

Segmentation task using deep learning (DL) has brought a tremendous impact on medical fields^{2, 4, 6}. Even though DL method for segmentation has high performance, it performs poorly on the small objects and boundaries of the object⁹. To solve this problem, we developed a combined methodology which utilizes deep learning segmentation algorithm and uncertainty quantification, to improve the segmentation results particularly for the poorly segmented regions such as boundaries and small lesions. Though there have been some uncertainty measurement researches on multiple sclerosis lesion¹¹ and ischemic stroke lesion⁷, there was no study on brain tumor. In this study, we present an interpretable and reliable method for brain tumor segmentation based on four types of uncertainties. This method can selectively maximize either precision or recall by including or excluding uncertain abnormal regions, especially on small lesions and the boundaries of the lesion.

Methods

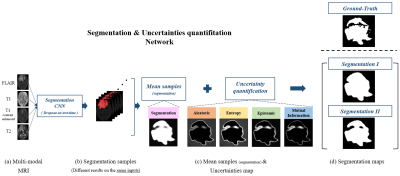
[MRI Dataset] We used BraTS 2018 training dataset² that include multi-contrast (FLAIR, T1, T1c, and T2) MR images of 255 subjects and manually segmented maps of tumor regions for each subject. 220 subjects’ data were used for the training set and 35 subjects' data were used for the validation set. In the analysis, the tumor voxel ratio of each patch was classified into small (<1%), medium (1~3%), and large (>3%).

[Segmentation] We segmented each patch into normal and complete tumor regions which consist of necrotic tumor, enhancing tumor, non-enhancing tumor and edema. Figure 1 shows the whole process of our method step by step. The network inputs were multi-contrast MRI images (FLAIR, T1, T1c, and T2) and the outputs of network were tumor segmentation samples. To sample different segmentation results on the same inputs, a Monte-Carlo dropout sampling^{1, 10} was applied. Dropout¹², randomly disconnecting some neurons in the network, is activated not only training time but also inference time. When inferred, inputs were forwarded multiple times while different dropouts applied, which sampled different segmentation results. The segmentation samples were averaged and then applied the optimal threshold (= 0.35) chosen from an ROC curve to generate a binary segmentation map (denoted as Segmentation I; Figure 2). The loss function for the network was Dice-Coefficient (DSC) defined by
$$DSC = \frac{2\sum_{i}^{N}p_{i}g_{i}}{\sum_{i}^{N}p_{i}^{2}+\sum_{i}^{N}g_{i}^{2}}$$
where p_i is the binary value of the i^th voxel in the segmentation output and g_i is the binary value of the i^th voxel in the ground truth.

[Uncertainty Quantification] To quantify four types of uncertainty maps, segmentation samples from different segmentation results on the same inputs are needed. Those sampled results were used to quantify four types of the uncertainties as follows^{1, 10, 11}
$$\begin{align*}& Aleatoric\ uncertainty:\qquad Al[y|x, W_{t}] \ \ =\sum_{c=1}^{C}\frac{1}{T}\sum_{t=1}^{T}y_{t}\odot (1-y_{t}) \\& Epistemic\ uncertainty:\quad \ \ Ep[y|x, W_{t}]\ = \sum_{c=1}^{C}\frac{1}{T}\sum_{t=1}^{T}[y_{t}- E(y)]^{\bigotimes 2} \\& Entropy:\qquad \qquad \qquad \qquad H[y|x, W_{t}] \ \ \ \approx -\sum_{c=1}^{C}\frac{1}{T}\sum_{t=1}^{T}p(y=c|x,w_{t})log_{2}(\frac{1}{T}\sum_{t=1}^{T}p(y=c|x,W_{t})) \\& Mutual information:\qquad \ \ MI[y|x, W_{t}] \ \approx H[y|x,W_{t}]-E[H[y|x,W_{t}]] \\\end{align*}$$
where T (= 50) is the number of sampling, C (= 2) is the number of categories, and is the segmentation sample in the tth network output. Aleatoric uncertainty is a measurement that reflects the confidence of the predicted segmentation. Epistemic uncertainty is the variance of the segmentation samples. Entropy is a measurement of how much information is in the model predictive density function at each voxel. Mutual information is a measurement that represents a relationship between the model posterior density function and prediction density function. Those results are voxel-wise maps that quantify uncertainty on segmentation results. Each uncertainty map can be converted to binary map applied by the optimal threshold (0.72 for aleatoric, 0.98 for epistemic, 0.82 for entropy, 0.68 for mutual information), chosen from the ROC curve, for each of uncertainty metrics. Finally, another segmentation map (Segmentation II) was generated by subtracting the thresholded uncertainty map from Segmentation I (Figure 2)

Results and discussion

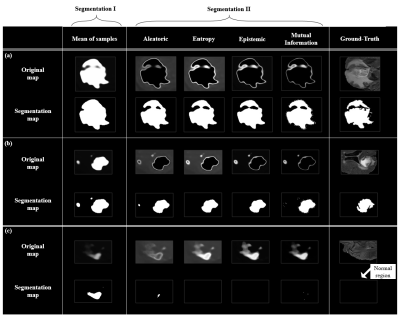
Figure 3 shows the representative cases presenting four types of the uncertainty maps and the corresponding segmentation maps. Figure 3a,b shows that segmentation II predicts tumor regions more precisely. Also Figure 3c shows that false positive regions can be effectively minimized using segmentation II results rather than Segmentation I. Table1 shows the precision (=$$$\frac{True Positive}{True Positive + False Positive}$$$) and recall (=$$$\frac{True Positive}{True Positive + False Negative}$$$) results of segmentation I & II based on lesion size. Table1 indicates that one can choose to improve precision while decreasing recall and vice versa. Specifically, the precision of Segmentation I decreases as the size of lesions decreases, while Segmentation II improves the precision by 5.9% (small), 3.4% (medium) and 2.6% (large) in average (Table 1).

Conclusion

In this work, we developed a methodology for segmenting brain tumor combining deep learning and uncertainty measurements. Our method can provide reliable diagnosis results especially for small lesions and boundaries of lesion.

Acknowledgements

This work was supported by the Brain Korea 21 Plus Project in 2019.
This research was supported by Basic Science Research Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Science, ICT & Future Planning (2017R1A2B2008412).