1787
Evaluating VoxelMorph, a deep learning-based non-linear diffeomorphic registration algorithm, against native ANTs SyN1McConnell Brain Imaging Centre, Montreal Neurological Institute and Hospital, Montreal, QC, Canada, 2Department of Biomedical Engineering, McGill University, Montreal, QC, Canada, 3Department of Neurology and Neurosurgery, McGill University, Montreal, QC, Canada
Synopsis
VoxelMorph is a deep-learning based non-linear diffeomorphic registration algorithm which claims to perform comparably to the state-of-the-art. However, the previous evaluation did not compare against manual gold-standard anatomical segmentations, used only the Dice metric for comparison, and compared against a modified version of a state-of-the-art algorithm, ANTs SyN. Here, VoxelMorph is evaluated against an unmodified version of ANTs SyN using multiple metrics based on manual labels. Results show VoxelMorph is less robust than ANTs SyN and underperforms in the presence of simulated deformations, and in registration of BrainWeb20 images to the VoxelMorph atlas.
Introduction
Image registration is the process of aligning two or more images from different time points, subjects, or modalities, into the same space1 and is a fundamental step in many medical image processing applications, including diagnostics, treatment, and monitoring of various brain pathologies, as well as image-guided surgical planning and intra-operative brain shift correction2. Non-linear diffeomorphic registration is capable of large and small deformations of brain images while preserving topology3, but tends to suffer from long computation times.Recently, deep learning has shown success in a wide variety of medical image processing tasks, including registration4. VoxelMorph is a deep learning-based non-linear diffeomorphic registration algorithm promising fast, topology-preserving registration of brain images comparable to state-of-the-art algorithms, such as the symmetric image normalization method by Advanced Normalization Tools (ANTs SyN)5. However, the previous evaluation performed between VoxelMorph and ANTs SyN could be improved. First, the training and testing of the VoxelMorph model was performed using fully automatic FreeSurfer-based segmentations of MRI volumes5, and not manual gold standard segmentations6. Thus, errors in automatic segmentation could confound registration quality metrics. Second, the smoothness parameters of the ANTs SyN algorithm were altered to be more similar to those of VoxelMorph5, thus restraining ANTs SyN's capacity to achieve a successful registration. Finally, the previous comparison was based only on Dice scores, which alone is not a complete evaluation of goodness-of-fit6.
Here, VoxelMorph is compared to native ANTs SyN in two experiments; first, using simulated deformations of the VoxelMorph atlas, and second, using a digital phantom database with manual gold standard labels – BrainWeb207. The methods are compared using Dice and Hausdorff metrics as well as the standard deviation of intensity between difference images, yielding a more comprehensive evaluation.
Methods
Data for the first experiment was generated from the VoxelMorph atlas8 by iteratively applying random Gaussian deformations at ten plausible average displacement severities ranging from 0 to 5 mm, following data augmentation methods9, yielding 70 deformed MR images.BrainWeb20, which comprises twenty T1-weighted digital MR phantoms created from twenty normal adults7 was used for the second experiment. For each of the 20 subjects, the ten manually corrected fuzzy mask brain structure volumes were used to simulate T1w MRI volumes. The MRI volumes underwent skull stripping, affine registration to the VoxelMorph atlas, and intensity normalization (as done for VoxelMorph5).
Both experiments underwent atlas-based registration, using the VoxelMorph atlas as the target volume for (1) the VoxelMorph model and (2) ANTs SyN with its default smoothing parameters. For both methods, the deformed output MR images and their warps were saved and applied to the corresponding image labels.
For the first experiment, warped labels were compared to the original VoxelMorph atlas labels to test each methods performance in the presence of deformation. For the second experiment, evaluation was performed by comparing the warped BrainWeb20 labels of the registered subjects to each other in the target space. For both databases, registration quality was measured by the intensity difference between the output and the target image. Comparison metrics for both databases include: Hausdorff distance, Cohen’s Kappa, and Dice score, calculated using the EvaluateSegmentation tool10.
Results and Discussion
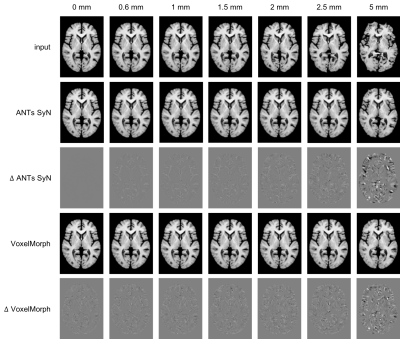
VoxelMorph takes approximately 30 seconds to register each image, while ANTs SyN takes approximately 43 minutes.Figure 1 depicts the deformed input volumes, and the recovered outputs from VoxelMorph and ANTs SyN, along with intensity difference images for Experiment 1. ANTs SyN demonstrated superior performance at all deformation magnitudes (p < 0.05) except 5 mm, indicating more accurate registrations.
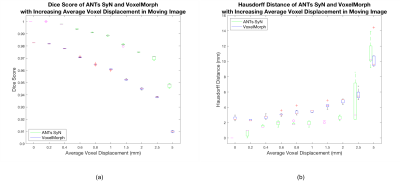
Figure 2 depicts boxplots of measured whole brain Dice scores and Hausdorff distances for Experiment 1. ANTs SyN yields better Dice scores for all simulated deformations and better Hausdorff distances for all but the 5 mm deformation, where there is no difference. Two 2-way repeated measures ANOVA performed on Dice score and Hausdorff distance, respectively, reveal significant differences between ANTs SyN and VoxelMorph (p < 0.01).
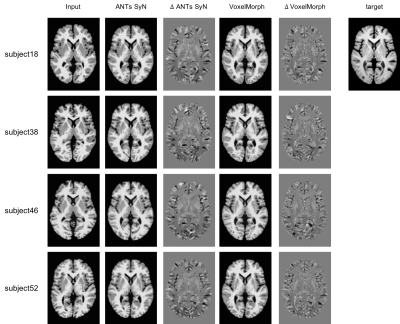
Figure 3 depicts the preprocessed BrainWeb20 inputs, and the outputs and difference images for VoxelMorph and ANTs SyN for four subjects in Experiment 2. Average standard deviation intensity differences confirm better performance for VoxelMorph (p < 0.05), as seen visually in the figure.
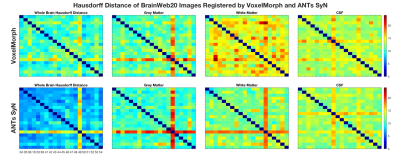
Figures 4 and 5 depict the Dice scores and Hausdorff distances, respectively, of whole brain, grey matter, white matter, and cerebral spinal fluid (CSF) BrainWeb20 labels. Dice scores are consistent across both methods in the inter-subject comparison (Figure 4), where ANTs SyN significantly outperforms VoxelMorph (p < 0.001). Inconsistent Hausdorff distances in white matter labels (Figure 5) suggest reduced robustness from VoxelMorph, whereas ANTs SyN shows more consistency and better performance for all tissues (p < 0.001). Poorer Hausdorff distance comparisons in Subjects 43 (for CSF) and 49 (all tissues), in both methods (Figure 5), are due to anatomical variability and poor registration, respectively.
Conclusion
This evaluation of VoxelMorph and ANTs SyN shows statistically better performance for ANTs SyN using Dice and Hausdorff distance metrics, and mixed results using intensity differences. Further evaluation, using more direct metrics of registration error with additional MRI data are needed.Acknowledgements
The authors would like to acknowledge funding from the Canadian Institutes of Health Research (CIHR), the Natural Sciences and Engineering Research Council (NSERC), and Healthy Brains for Healthy Lives (HBHL). The authors would also like to thank the Department of Biomedical Engineering, and the Faculty of Medicine at McGill University for their financial aid.References
1. B. Zitová and J. Flusser, “Image registration methods: a survey,” Image Vis. Comput., vol. 21, no. 11, pp. 977–1000, Oct. 2003.
2. J. B. A. Maintz and M. A. Viergever, “A survey of medical image registration,” Med. Image Anal., vol. 2, no. 1, pp. 1–36, 1998.
3. M. Wang and P. Li, “A Review of Deformation Models in Medical Image Registration,” J. Med. Biol. Eng., vol. 39, no. 1, pp. 1–17, 2019.
4. G. Haskins, U. Kruger, and P. Yan, “Deep Learning in Medical Image Registration: A Survey.”
5. A. V. Dalca, G. Balakrishnan, J. Guttag, and M. R. Sabuncu, “Unsupervised learning for fast probabilistic diffeomorphic registration,” Lect. Notes Comput. Sci. (including Subser. Lect. Notes Artif. Intell. Lect. Notes Bioinformatics), vol. 11070 LNCS, pp. 729–738, 2018.
6. A. Fenster and B. Chiu, “Evaluation of segmentation algorithms for medical imaging,” Annu. Int. Conf. IEEE Eng. Med. Biol. - Proc., vol. 7 VOLS, pp. 7186–7189, 2005.
7. B. Aubert-Broche, M. Griffin, G. B. Pike, A. C. Evans, and D. L. Collins, “Twenty new digital brain phantoms for creation of validation image data bases,” IEEE Trans. Med. Imaging, vol. 25, no. 11, pp. 1410–1416, 2006.
8. R. Sridharan et al., “Quantification and analysis of large multimodal clinical image studies: Application to stroke,” Lect. Notes Comput. Sci. (including Subser. Lect. Notes Artif. Intell. Lect. Notes Bioinformatics), vol. 8159 LNCS, pp. 18–30, 2013.
9. P. Novosad, V. Fonov, D. Louis Collins, T. Alzheimer’s Disease, and N. Initiative, “Accurate and robust segmentation of neuroanatomy in T1-weighted MRI by combining spatial priors with deep convolutional neural networks,” 2019.
10. A. A. Taha and A. Hanbury, “Metrics for evaluating 3D medical image segmentation: Analysis, selection, and tool,” BMC Med. Imaging, vol. 15, no. 1, 2015.
Figures